| Высшее образование |
Планирование экспериментов
4.8. Точность и количество реализаций модели при зависимом ряде данных
До сих пор мы предполагали, что выходные данные модели образуют ряд значений 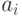 , статистически независимых и принадлежащих одному закону распределения. Однако это не всегда так.
, статистически независимых и принадлежащих одному закону распределения. Однако это не всегда так.
Пусть, например, целью статистического моделирования будет определение матожидания времени пребывания заявки в очереди 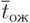 одноканальной системы массового обслуживания.
одноканальной системы массового обслуживания.
В результате эксперимента с моделью будет получен ряд значений 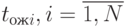 , которые заведомо статистически зависимы:
, которые заведомо статистически зависимы:
при большом времени ожидания  -й заявки значение
-й заявки значение  , не может быть малым, если обе заявки находились одновременно в очереди. Связь точности оценки
, не может быть малым, если обе заявки находились одновременно в очереди. Связь точности оценки  , среднего времени ожидания
, среднего времени ожидания 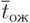 с количеством реализаций
с количеством реализаций  в этом случае выглядит иначе, чем было рассмотрено ранее. Мы рассмотрим метод определения точности и количества реализаций для статистически зависимых последовательностей - откликов модели, в основе которого лежит так называемый регенеративный анализ.
в этом случае выглядит иначе, чем было рассмотрено ранее. Мы рассмотрим метод определения точности и количества реализаций для статистически зависимых последовательностей - откликов модели, в основе которого лежит так называемый регенеративный анализ.
Допустим, что в результате эксперимента с имитационной моделью получен ряд значений  , приведенный в табл. 4.7.
, приведенный в табл. 4.7.
Здесь  - порядковый номер поступающих заявок.
- порядковый номер поступающих заявок.

|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
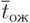
|
0 | 5 | 7 | 0 | 3 | 0 | 3 | 9 | 11 | 2 | 0 | … |
Обратим внимание на то, что заявка 1 застает канал обслуживания свободным: ее время ожидания в очереди равно нулю. Такая же ситуация возникла для заявок 4, 6 и 11. Период занятости и простоя канала обслуживания образуют цикл его работы. В табл. 4.7 можно выделить три таких цикла, в которые входят следующие наборы обслуженных заявок:
- цикл 1 - заявки 1, 2, 3;
- цикл 2 - заявки 4, 5;
- цикл 3 - заявки 6, 7, 8, 9, 10.
Заявка 11 является началом нового цикла 4 и т. д.
Начала каждого цикла неотличимы друг от друга - заявка поступает на обслуживание без ожидания. Говорят так: система восстанавливается (регенерируется) к началу каждого цикла, следовательно, поведение системы в очередном цикле не зависит от ее поведения в предыдущих циклах.
Введем обозначения:
 - сумма времен ожидания
- сумма времен ожидания  -го цикла,
-го цикла,  ;
;
 - количество заявок, образующих
- количество заявок, образующих  -й цикл. Для данных, приведенных в табл. 4.5:
-й цикл. Для данных, приведенных в табл. 4.5:
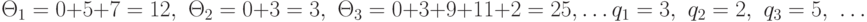
Таким образом, мы получили пары чисел - независимых и одинаково распределенных:
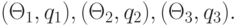
Заметим, что числа  и
и  между собой зависимы.
между собой зависимы.
Целью дальнейших рассуждений является определение оценки
матожидания времени пребывания заявки в очереди 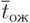 , отличающееся от
, отличающееся от ![M [t_{ож}]](/sites/default/files/tex_cache/5f50ca9c6e82c39acaf1c2bfdee70159.png) на величину не более
на величину не более  при заданной достоверности
при заданной достоверности  . Так как
. Так как
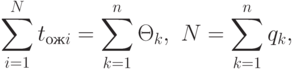
где  - число циклов, то оценка матожидания времени пребывания заявки в очереди определяется так:
- число циклов, то оценка матожидания времени пребывания заявки в очереди определяется так:
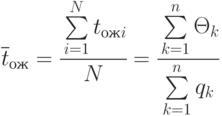
Разделим числитель и знаменатель на число циклов  и получим:
и получим:
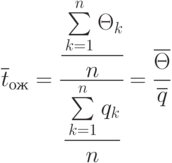
В соответствии с центральной предельной теоремой оценка длительности цикла  при числе циклов
при числе циклов 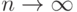 есть случайная величина, распределенная по нормальному закону с математическим ожиданием и дисперсией соответственно:
есть случайная величина, распределенная по нормальному закону с математическим ожиданием и дисперсией соответственно:
![M[\overline{\Theta}]=M[\Theta], \sigma_{\overline{\Theta}}^{2}=\cfrac{\sigma^2}{n}](/sites/default/files/tex_cache/3e6974e5e9904af6fd0168d244d08d48.png)
где  - дисперсия, представляющая собой сумму дисперсий зависимых между собой случайных величин
- дисперсия, представляющая собой сумму дисперсий зависимых между собой случайных величин  и
и 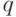 .
.
Следовательно, имеет место уже знакомое нам выражение
![P\left ( |\overline{\Theta}-M[{\Theta}]| < t_{\sigma}\cfrac{\sigma}{\sqrt{n}} \right ) =
2\Phi (t_{sigma})](/sites/default/files/tex_cache/6ea9a4575657a87a053adb1e0d4bbafd.png)
Если  - граничное значение ошибки для оценки
- граничное значение ошибки для оценки 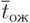 , то очевидно граничное значение ошибки для оценки
, то очевидно граничное значение ошибки для оценки  равно
равно 
Тогда 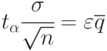 . Из этого следует:
. Из этого следует:
Коэффициент 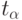 , как и ранее, характеризует достоверность оценки
, как и ранее, характеризует достоверность оценки 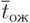 и является аргументом функции Лапласа:
и является аргументом функции Лапласа:
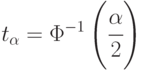
Значения  и
и 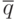 до эксперимента неизвестны. Их ориентировочные значения должны быть определены по данным предварительных прогонов модели в количестве
до эксперимента неизвестны. Их ориентировочные значения должны быть определены по данным предварительных прогонов модели в количестве 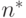 реализаций циклов. Обычно
реализаций циклов. Обычно 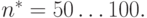
Оценку дисперсии  обозначим
обозначим 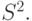 Она вычисляется так:
Она вычисляется так:

Здесь:
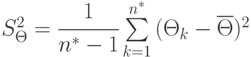 - оценка дисперсии
- оценка дисперсии  ;
;
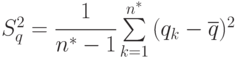 - оценка дисперсии
- оценка дисперсии  ;
;
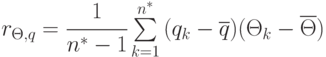 - корреляционный момент случайных величин
- корреляционный момент случайных величин  и
и  ;
;
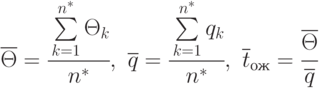
И, наконец, необходимое число циклов будет определено:
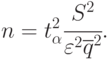
Если окажется  , то моделирование продолжается до достижения
, то моделирование продолжается до достижения  циклов. Если же окажется
циклов. Если же окажется  то моделирование заканчивается и, если необходимо, дается оценка достигнутой точности.
то моделирование заканчивается и, если необходимо, дается оценка достигнутой точности.
Признак конца моделирования: 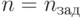 или количество обслуженных СМО заявок
или количество обслуженных СМО заявок 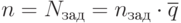 .
.
4.9. Проблема начальных условий
К тактическому планированию эксперимента относится и решение так называемой проблемы начальных условий.
В отличие от реальной системы модель работает прогонами - для накопления нужной статистики. Поэтому при каждом новом прогоне модели требуется какое-то время, чтобы установился стационарный режим, характеристики которого интересуют исследователя.
То есть начальные условия искажают характеристики стационарного режима.
Например, моделируется функционирование направления связи. В установившемся режиме входной буфер направления имеет среднее заполнение поступившими, но не обработанными пока сообщениями. Но перед каждым очередным прогоном в модели устанавливаются нулевые начальные условия.
Или еще: вероятность обслуживания заявки в СМО имеет какое-то стационарное значение. Но в начальный момент эта вероятность равна нулю.
Следовательно, начальные установки регистрируемого параметра (показателя эффективности и др.) искажают результат.
Для устранения ошибок, вызываемых не соответствующей установкой начальных условий, возможно применение следующих мер:
- Ставить начальные условия, близкие значениям стационарного режима, то есть модель разрабатывается так, что условия функционирования системы типичны с самого начала.
- Увеличить интервал исследования (
 ) так, чтобы он стал значительно больше предполагаемого времени установления стационарного режима.
) так, чтобы он стал значительно больше предполагаемого времени установления стационарного режима. - Отбросить информацию, снимаемую в промежутке времени от пуска (
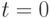 ) до установившихся стационарных значений, и продолжить моделирование, собирая статистику, на которую уже не влияют нетипичные ситуации.
) до установившихся стационарных значений, и продолжить моделирование, собирая статистику, на которую уже не влияют нетипичные ситуации.
Первый подход требует от разработчика знания типичных условий работы и умения внести в модель эти условия. В моделях сложных систем это вряд ли выполнимо.
При втором подходе требуется слишком долгое моделирование до наступления такого состояния, когда исчезает влияние собранных неверных данных. Стоимость такого моделирования для сложных систем может оказаться слишком высокой, что делает этот подход нежелательным.
Третий подход оказывается наиболее удобным. Нужно на определенной стадии моделирования отбросить статистику с последующим продолжением моделирования без каких-либо модификаций модели. Такой подход используется в ряде систем моделирования. Заметим, однако, что время установки стационарных значений в модели трудно определить до эксперимента.
Все эти приемы могут уменьшить влияние переходных процессов в модели на результаты эксперимента, однако свести его к нулю не могут.
Вопросы для самоконтроля
- Что понимается под компьютерным экспериментом?
- Каковы цели планирования экспериментов?
- Что такое стратегическое и тактическое планирование?
- Что понимается под кибернетическим представлением эксперимента?
- Что такое реакция или отклик системы?
- Что такое факторы и уровни факторов?
- Приведите вариант классификации факторов.
- Симметричный факторный эксперимент.
- Полный факторный эксперимент (ПФЭ).
- Как определяется количество информационных точек в ПФЭ? В симметричном ПФЭ?
- Пути сокращения затрат на проведение эксперимента.
- Дайте определение точности и достоверности оценки характеристики случайной величины.
- Как получено выражение, связывающее точность и достоверность оценки с числом реализаций модели?
- Способы априорного определения оценки дисперсии.
- Как получено выражение
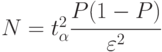 ? Что означают аргументы этого выражения?
? Что означают аргументы этого выражения? - Способы априорного определения вероятности
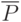 .
. - В результате прогонов имитационной модели ожидается получить три случайных показателя со следующими характеристиками:
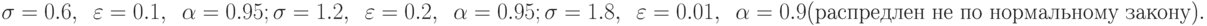
Определить требуемое количество
 реализаций модели для достижения требуемой точности и достоверности.
реализаций модели для достижения требуемой точности и достоверности. - В чем состоит проблема начальных условий, и каковы пути ее разрешения?
