| Высшее образование |
Типовые математические модели
2.8. Элементарные модели боя
Приемлемая по точности математическая модель такой сложной системы как бой невозможна из-за наличия неопределенных и неформализуемых факторов и уникальных ситуаций. Однако, приблизительные частные модели возможны и целесообразны для количественного обоснования некоторых решений, оценки обстановки, прогнозирования результатов решений и др.
Рассмотрим некоторые элементарные модели боя.
2.8.1. Модель высокоорганизованного боя
Постановка задачи
Две группировки А и Б ведут бой. В составе группировок А и Б  и
и 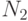 боевых единиц со скорострельностями
боевых единиц со скорострельностями 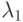 и
и  и вероятностями поражения цели при одном выстреле
и вероятностями поражения цели при одном выстреле 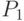 и
и  соответственно. Каждая группировка однородна, но не обязательно группировки однородны между собой. Например, бой танков с танками, танков с противотанковыми средствами, истребителей с бомбардировщиками и т. п.
соответственно. Каждая группировка однородна, но не обязательно группировки однородны между собой. Например, бой танков с танками, танков с противотанковыми средствами, истребителей с бомбардировщиками и т. п.
Высокоорганизованным боем называют бой с полной информацией, а именно:
- любая боевая единица одной стороны, пока она не поражена, может вести огонь по любой непораженной боевой единице другой стороны;
- разведка, связь и управление идеальны, то есть перенос огня каждого средства на новую цель происходит мгновенно после поражения предыдущей цели;
- пораженная боевая единица в дальнейших действиях не участвует, то есть за время боя не восстанавливается, пополнения сторон нет;
- временем полета носителя заряда пренебрегаем;
- перенос огня не влияет на скорострельность и вероятность поражения;
- количество боеприпасов неограниченно;
- противоборствующие группировки достаточно многочисленны (это необходимое допущение будет обосновано при моделировании).
При этих допущениях процесс динамики боя двух группировок может рассматриваться как случайный марковский процесс с дискретными состояниями и непрерывным временем, для которого могут быть получены уравнения динамики средних, позволяющие определить для любого момента времени средние численности сторон.
Цель моделирования. Прогнозирование средних количеств пораженных и непораженных боевых единиц каждой группировки на любой момент времени.
Моделирование
Описание состояний одной боевой единицы
Каждое средство противоборствующих сторон А и Б может находиться в одном из двух состояний соответственно:
 - не поражено;
- не поражено;
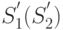 - поражено.
- поражено.
Построение размеченных графов состояний
Графы состояний для каждой группировки элементарны (рис. 2.21).
Интенсивность 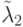 - интенсивность потока поражающих выстрелов стороны Б, приходящихся на одну боевую единицу стороны А, то есть переводящих ее из состояния
- интенсивность потока поражающих выстрелов стороны Б, приходящихся на одну боевую единицу стороны А, то есть переводящих ее из состояния  в состояние
в состояние  .
.
Аналогичные рассуждения объясняют 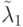 . Очевидно, для начального состояния (
. Очевидно, для начального состояния (  ):
):
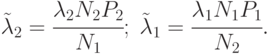
Составление уравнений динамики средних
В ходе боя численности боеспособных единиц сторон будут случайным образом изменяться (уменьшаться, так как пополнение средств поражения сторон мы пока не рассматриваем). Обозначим эти случайные численности каждой стороны 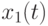 и
и  соответственно. Тогда:
соответственно. Тогда:
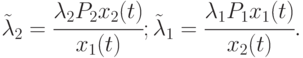
Зависимость  и
и 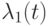 от случайных значений
от случайных значений  и
и 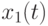 делает аналитическое решение задачи практически невозможным. Поэтому, используя принцип квазирегулярности, заменим
делает аналитическое решение задачи практически невозможным. Поэтому, используя принцип квазирегулярности, заменим  и
и 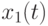 их матожиданиями
их матожиданиями 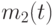 и
и 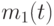 .
.
Заметим, что 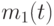 и
и 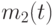 являются целью моделирования.
являются целью моделирования.
После замены выражения для 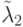 и
и 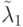 принимают вид:
принимают вид:

Запишем уравнения динамики средних для состояний  и
и 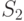 :
:

Для состояний  и
и 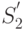 уравнения не нужны, так как средние численности этих состояний
уравнения не нужны, так как средние численности этих состояний 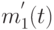 и
и  однозначно связаны с
однозначно связаны с 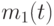 и
и 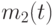 :
:
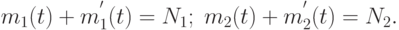
После очевидного упрощения уравнения динамики средних принимают вид:

Здесь и далее для лучшей обозримости аргумент  в
в 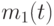 и
и 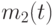 опустим.
опустим.
Систему уравнений (2.3) обычно называют уравнениями динамики боя, иногда - уравнениями Ланчестера. Ланчестер - полковник английской армии времен первой мировой войны. Именно он предложил излагаемые подходы формализации боевых действий.
Решение уравнений динамики средних
Искомые численности сторон  и
и 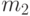 находятся интегрированием системы (2.3) при начальных условиях:
находятся интегрированием системы (2.3) при начальных условиях:
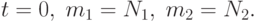
Решение имеет вид:
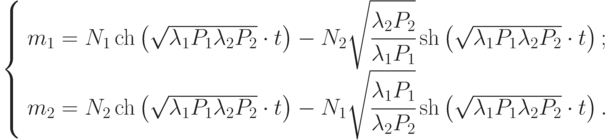
Для лучшей обозримости введем обозначения:
 - эффективная скорострельность стороны А;
- эффективная скорострельность стороны А;
 - эффективная скорострельность стороны Б.
- эффективная скорострельность стороны Б.
Эффективные скорострельности характеризуют плотности потоков успешных выстрелов соответствующей стороны.
 - доля боеспособных единиц стороны А;
- доля боеспособных единиц стороны А;
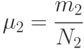 - доля боеспособных единиц стороны Б;
- доля боеспособных единиц стороны Б;
 - коэффициент преимущества стороны А над стороной Б;
- коэффициент преимущества стороны А над стороной Б;
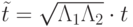 - приведенное время.
- приведенное время.
С учетом этих обозначений решение модели высокоорганизованного боя выглядит так:

Графически варианты решений модели в зависимости от коэффициента превосходства представлены на рис. 2.22.
Из формул видно, что убывание численности группировок в большей мере зависит от соотношения сил 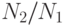 , чем от соотношения эффективных скорострельностей
, чем от соотношения эффективных скорострельностей 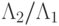 : первое отношение входит в формулы непосредственно, а второе - под знаком корня. Увеличение начальной численности
: первое отношение входит в формулы непосредственно, а второе - под знаком корня. Увеличение начальной численности  в два раза удваивает параметр
в два раза удваивает параметр 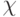 , тогда как удвоение
, тогда как удвоение  увеличивает
увеличивает 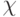 только в
только в 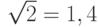 раза. Поэтому повышение скорострельности менее выгодно.
раза. Поэтому повышение скорострельности менее выгодно.
В рамках данной модели при  выигрывает бой сторона А, при
выигрывает бой сторона А, при  - сторона Б.
- сторона Б.
Кривые 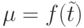 на рис. 2.22 оборваны до достижения нуля, так как при малочисленных группировках метод динамики средних дает большие ошибки.
на рис. 2.22 оборваны до достижения нуля, так как при малочисленных группировках метод динамики средних дает большие ошибки.
Если силы сторон равны (  ), то динамика сохранения сил сторон одинакова;
), то динамика сохранения сил сторон одинакова;  в любой момент боя. Бой будет продолжаться до определенного уровня истощения сил, после чего неизбежны попытки политического решения конфликта.
в любой момент боя. Бой будет продолжаться до определенного уровня истощения сил, после чего неизбежны попытки политического решения конфликта.
В рамках этой модели бой заканчивается разгромом слабой стороны тем быстрее, чем больше превосходство другой. Победа в этой модели достигается числом, не уменьем. Не учитывается опыт, способности командиров, обученность личного состава. Впрочем, параметр  косвенно учитывает обученность экипажей средств поражения.
косвенно учитывает обученность экипажей средств поражения.
Пример 2.11. Группировка, в составе которой 270 противотанковых средств (ПТС), находится в обороне. Скорострельность каждого ПТС 6 выстр./мин, вероятность поражения одним ПТС одного танка равна 0,3. Скорострельность танка 4 выстр./мин, вероятность поражения одним танком одного ПТС 0,25 при коэффициенте превосходства 1,2.
Спрогнозировать, сколько нужно танков, чтобы прорвать оборону при полном уничтожении ПТС группировки.
Решение
Известно, что

откуда
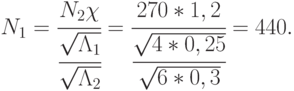
Заметим, коэффициент преимущества 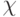 не имеет иного смысла, кроме упрощения формул для вычисления
не имеет иного смысла, кроме упрощения формул для вычисления 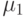 и
и 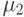 . Поэтому результаты расчетов не имеют оперативно-тактического обоснования.
. Поэтому результаты расчетов не имеют оперативно-тактического обоснования.
Задача 2.12. Сторона А имеет 30 огневых средств со скорострельностью каждого 5 выстр./мин и вероятностью поражения 0,2. Сторона Б имеет 40 огневых средств со скорострельностью каждого 4 выстр./мин и вероятностью поражения 0,3.
Провести расчеты для прогноза исхода боя, времени его окончания и количества сохранившихся огневых средств у победившей стороны.
Решение
Исходные данные

Прогнозирование исхода боя
Составим соотношения превосходства сторон:

Так как 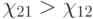 , то преимущество будет у стороны Б, то есть победить должна сторона Б.
, то преимущество будет у стороны Б, то есть победить должна сторона Б.
Прогнозирование времени окончания боя
Бой продолжается до полной победы, то есть  или из (2.4)
или из (2.4)

Учтем, что  , откуда
, откуда
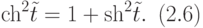
С другой стороны, из (2.5)  .
.
Из выражений (2.5) и (2.6) имеем:

Так как  , то
, то 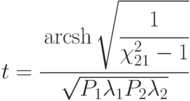 .
.

Определение количества огневых средств, сохранившихся у стороны Б

Так как из выражения (2.5)  , то
, то
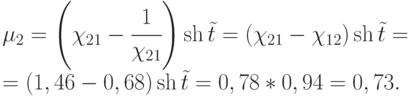
Теперь  .
.
К концу боя у стороны Б останется от 29 до 30 огневых средств, тогда как огневые средства стороны А будут полностью уничтожены.
Приведенные результаты прогноза исхода боя двух группировок являются приблизительными, оценочными, так как при малых количествах огневых средств (  ) метод динамики средних, лежащий в основе уравнений динамики боя, может давать существенные ошибки.
) метод динамики средних, лежащий в основе уравнений динамики боя, может давать существенные ошибки.


