| Экстернат |
M. ZIP
PGP использует методику сжатия данных ZIP, созданную Джином Гэйлеем, Марком Адиром и Ричардом Уользом. Она базируется на алгоритме, называемом LZ77 (Lempel-Ziv 77), который был изобретен Джакопом Зивом (Jacop Ziv) и Абрахамом Лемпэлем (Abraham Lempel). В этом приложении мы кратко обсуждаем LZ77.как основу ZIP.
М. 1. Кодирование LZ77
Кодирование LZ77 - пример кодирования на основе словаря. Идея в том, что нужно создать словарь (таблицу) строк, используемых в течение сеанса связи. Если и передатчик, и приемник имеют копию словаря, то уже встречавшиеся строки могут быть заменены их индексами в словаре, чтобы уменьшить количество переданной информации.
Хотя идея кажется простой, она довольно сложна в реализации. Первое: как создать словарь для каждого сеанса? Он не может быть универсальным из-за своей длины. Второе: как приемник может приобрести словарь, созданный передатчиком? Если вы передаете словарь, вы посылаете дополнительные данные, которые вредят цели сжатия.
Практический алгоритм, который использует идею адаптивного кодирования на основе словаря, - LZ77-алгоритм. Мы приводим основную идею этого алгоритма с примером, но не копаемся в деталях различных версий и реализаций. В нашем примере предположим, что нам нужно передать следующую строку. Мы выбрали эту строку, чтобы упростить обсуждение.
BAABABBBAABBBBAA
Для нашей простой версии LZ77-алгоритма процесс разделен на две фазы: сжатие строки и расширение (декомпрессия строки).
Сжатие
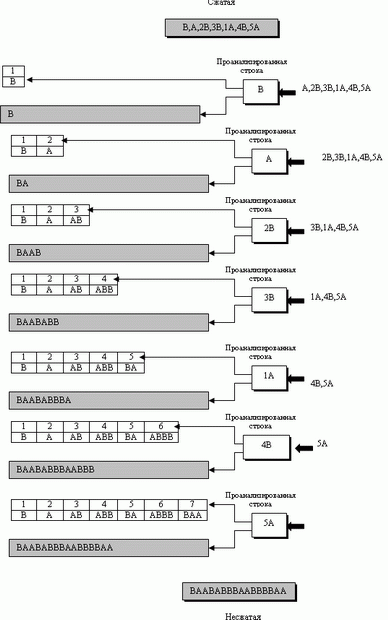
В этой фазе есть два параллельных события: создание индексированного словаря и сжатие строки символов. Алгоритм извлекает из памяти несжатую строку, у которой наименьшая подстрока - та, что не может быть найдена в словаре. Затем алгоритм сохраняет копию этой подстроки в словаре (как новый вход) и назначает значение индекса. Сжатие возникает, когда подстрока, если это не последний символ, заменена индексом, найденным в словаре. Процесс затем вставляет индекс и последний символ подстроки в сжатую строку. Например, если подстрока - ABBB, вы ищете в словаре ABB. Вы находите, что индекс для ABB - 4 ; сжатая подстрока поэтому будет 4B. Рисунок M.1 показывает процесс для нашей типовой строки.
Рассмотрим несколько шагов на рис. М.1.
- Шаг 1. Процесс извлекает из первоначальной строки наименьшую подстроку, который нет в словаре. Поскольку словарь пуст, наименьший символ - один символ (первый символ B ). Процесс хранит его копию как первый вход в этом словаре. Его индекс - 1. Часть этой подстроки не может быть заменена индексом из словаря (потому что это только один символ). Потому процесс вставляет B (без индекса) в сжатую строку. Пока сжатая строка имеет только один символ: B. Первоначальная строка сохраняется не в сжатом виде - без первого символа.
- Шаг 2. Процесс извлекает из оставшейся строки следующую наименьшую подстроку, которой нет в словаре. Эта подстрока - символ A, который не находится в словаре. Процесс хранит копию этого символа как второй вход в словаре. Часть этой подстроки не может быть заменена индексом из словаря (потому что это только один символ). Процесс вставляет в сжатую строку A. Теперь сжатая строка имеет два символа: B и A (мы поставили запятые между подстроками в сжатой строке, чтобы показать разделение).
- Шаг 3. Процесс извлекает из остающейся строки следующую наименьшую подстроку, которой нет в словаре. Эта ситуация отличается от двух предыдущих шагов. Следующий символ ( A ) находится в словаре, так что процесс извлекает два символа ( AB ), а этой комбинации в словаре нет. Процесс сохраняет копию AB как третий вход в словарь. Процесс теперь находит индекс входа в словаре и создает сжатую подстроку без последнего символа ( AB без последнего символа, т. е. без A ). Индекс для комбинации сжатой строки - 2, так что процесс вставляет в сжатую строку комбинацию 2B.
- Шаг 4. Затем процесс извлекает подстроку ABB (потому что и AB уже в словаре есть). Копия ABB сохраняется в словаре с присвоением индекса 4. Процесс находит индекс подстроки без последнего символа ( AB ) - это 3. В сжатую строку вставляется комбинация 3B. Вы, возможно, заметили, что в трех предыдущих шагах мы фактически не достигли никакого сжатия, потому что заменили один символ одним (в первом A на A и B на B во втором шаге) и два символа на два ( AB на 2B на третьем шаге). Но на этом шаге мы фактически уменьшили число символов ( ABB стал 3B ). Если первоначальная строка имеет много повторений (это предположение справедливо в большинстве случаев), мы можем заметно уменьшить число символов.
Каждый из остающихся шагов подобен одному из предыдущих четырех шагов, и мы предоставляем читателю возможность выполнить их самому. Обратите внимание, что словарь используется передатчиком, чтобы найти индексы. Его не передают приемнику; приемник должен создать словарь для себя сам, как мы увидим это в следующем разделе.
Декомпрессия
Декомпрессия - инверсия процесса сжатия. Процесс извлекает подстроки из сжатой строки и пробует заменять индексы соответствующими входами в словаре, который вначале является пустым и создается постепенно. Главное, что когда индекс получен, далее надо использовать вход словаря к соответствующему индексу. Рисунок M.2 показывает процесс декомпрессии.
Рассмотрим несколько шагов на рис. М.2.
- Шаг 1. Анализируется первая подстрока сжатой строки. Это - B без индекса. Поскольку подстрока не находится в словаре, она добавляется к словарю. Подстрока ( B ) вставляется в несжатую (декомпрессированную) строку.
- Шаг 2. Анализируется вторая подстрока ( A ); ситуация такая же, как и на шаге 1. Теперь несжатая строка имеет два символа ( BA ), и словарь имеет два входа.
- Шаг 3. Анализируется третья подстрока ( 2B ). Процесс ищет в словаре и заменяет индекс 2 подстрокой A. К несжатой строке добавляется новая подстрока ( AB ), и AB добавляется к словарю.
- Шаг 4. Анализируется четвертая подстрока ( 3B ). Процесс ищет в словаре и заменяет индекс 3 с подстрокой AB. Подстрока ABB теперь добавляется к несжатой строке, и ABB добавляется к словарю.
Мы не будем делать анализ последних трех шагов, а добавим как задание для самостоятельных упражнений.
Как вы заметили, мы используем для обозначения индекса десятичные числа, такие, как 1 или 2. В действительности индекс записывается в двоичном виде (возможно, в данном случае длинной 3) для лучшей эффективности.