НОУ ИНТУИТ | Управление ключами шифрования и безопасность сети. Лекция 5: E. Проблемы дня рождения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Ключевые слова: вероятность, значение

Проблемы дня рождения обсуждались в "лекции 1" . В этом приложении даются общие решения четырех проблем дней рождения - мы используем теорию вероятностей, некоторые положения которой кратко приведены в "приложении D" . Для того чтобы упростить решения, применяются следующие математические уравнения:

$1-x \approx e^{-x}// \ Ряд \ Тейлора \ при \ малом \ x \\ 1+2+ \dots + (k-1) = k(k-1) / 2 \\ k(k-1) \approx k^{2}$

E.1. Четыре проблемы

Мы представляем решения четырех проблем, обсужденных в "лекции 1" .

Первая проблема

Мы имеем множество выборок значений размером. k, в которых каждый элемент может иметь только одно из. N равновероятных значений. Каков должен быть минимальный размер выборки k в множестве, чтобы с вероятностью P > 1/2 по крайней мере один из элементов был бы равен заранее определенному значению? Чтобы решить проблему, мы сначала находим вероятность P, что по крайней мере один элемент равен заранее заданному значению. Затем задаем вероятность к 1/2, чтобы найти минимальный размер элемента.

Вероятность

Чтобы найти вероятность P, мы делаем четыре шага:

Если P_эл - вероятность того, что выбранный элемент равен заранее заданному значению, то P_эл = 1/N, потому что элемент может с равной вероятностью принимать любое из значений. N.
Если Q_эл - вероятность, что выбранный элемент не равен заранее заданному значению, то Q_эл = 1- P_эл = (1 - 1/ N).
Если каждый элемент независим (справедливое предположение) и Q - вероятность, что ни один элемент не равен заранее заданному значению, то Q = Q_эл ^k = (1 - 1/ N)^k.
Наконец, если P - вероятность того что, по крайней мере один элемент равен заранее определенному значению, то. P = 1- Q или P = 1 - (1 - 1/N)^k.

Размер выборки

Теперь мы находим минимальный размер выборки k, чтобы вероятность появления элемента была P >= 1/2. Как показано ниже, значение k должно быть k > ln2 x N:

P = 1 - (1 - 1/N)^k >= 1/2 -> (1 - 1/N)^k <= ?
(1 - 1/N)^k <= 1/2 -> e^-k/N <= 1/2

Используя аппроксимацию 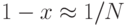$1 - x \approx 1/N$ при x = 1/N

e^-k/N <= 1/2 -> e^k/N >= 2 -> k/N >= ln(2) x N

Первая проблема

Вероятность: P = 1 - (1 - 1/N)^k Размер выборки: k >= ln2 >= N

Вторая проблема

Вторая проблема - та же самая, что и первая, за исключением того, что заранее заданное значение - один из элементов множества. Это означает, что мы можем найти результат второй проблемы, если заменим k на k - 1, потому что после выбора одного элемента из выборки элементов остается только. k - 1 элементов. Поэтому P = 1 - (1 - 1/N)^k-1 и. k> ln2 >= N + 1.

Вторая проблема

Вероятность: P = 1 - (1 - 1/N) ^k-1 Размер выборки k > ln2 >= N + 1.

Третья проблема

В третьей проблеме мы должны найти минимальный размер выборки элементов k, такой, чтобы с вероятностью P > 1/2 по крайней мере два элемента имели одно и то же значение. Чтобы решить проблему, мы сначала находим соответствующую вероятность P, затем задаем вероятность 1/2, чтобы найти минимальный размер выборки.

Вероятность

Здесь мы используем не такую стратегию, как в предыдущих случаях.

Мы определяем вероятности появления элементов по одному. Предположим, что P является вероятностью, с который выборка элементов . i имеет то же самое значение, что и одна из предыдущих выборок, и Q - вероятность, с который выборка i имеет значение, отличающееся от всех предыдущих выборок.
- Поскольку перед первой выборкой нет ни одной другой P₁= 0 и Q₁ = 1- 0 = 1.
- Поскольку перед второй выборкой есть одна другая выборка, первая и вторая выборки могут иметь одно из значений из N элементов. P₂ = 1/N и Q₂ = (1 - 1/N).
```
Q =Q₁ x Q₂ x Q₃ x ... x  Q_К= 1 x (1-1/N)x (1 - 2/N) x ... x (1 - (k-1)N)
Q = (e^-1/N) x (e^-1/N) x ... x (e^-(k-1)/N)
```
  Используем аппроксимацию 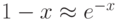$1 - x \approx e^{-x}$ при x = i/N
```
Q = e^-k(k-1)/2N
```
  Используем уравнение 1 + 2+ ... + (k-1) = k(k-1)/2
```
Q = e^-kk/2N
```
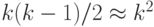
  Используем уравнение $k(k-1)/2 \approx k^{2}$
  
  Поскольку перед третьей выборкой есть две выборки, то каждая из этих двух выборок может иметь одно из значений.из N. элементов, P₃ = 2/N и Q₃ = (1- 2/N).
- Продолжая эти рассуждения, мы получим P_k = (k - 1)/N и Q_k = (1 - (k - 1)/N).
Предположим, что все выборки независимы, тогда вероятность Q, с которой все выборки имеют различные значения,

Q =Q₁ x Q₂ x Q₃ x ... x Q_К= 1 x (1-1/N)x (1 - 2/N) x ... x (1 - (k-1)N)

Q = (e^-1/N) x (e^-1/N) x ... x (e^-(k-1)/N)

Используем аппроксимацию 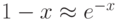$1 - x \approx e^{-x}$ при x = i/N

Q = e^-k(k-1)/2N

Используем уравнение 1 + 2+ ... + (k-1) = k(k-1)/2 Q = e^-kk/2N

Используем уравнение 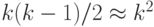$k(k-1)/2 \approx k^{2}$

Наконец, если P - вероятность, с которой по крайней мере две выборки имеют одни и те же значения, то мы имеем P = 1 - Q или P = 1 - e^-kk/2N

Размер выборки

Теперь мы можем найти минимальный размер выборки с вероятностью P >= 1/2. Она равна k >= (2 x ln2)^1/2 или k >= 1,18 x N^1/2, доказательство приведено ниже:

P = 1 - e^-kk/2N >= 1/2 -> e^-kk/2N <= 1/2
e^-kk/2N <=1/2 -> e^-kk/2N >= 2 -> k²/2N >= ln(2) -> k >= (2 x ln(2))^1/2 x N^1/2

Третья проблема

Вероятность: P = 1 - e^-kk/2N Размер выборки: k >= (2 x ln(2))^1/2 x N^1/2

Четвертая проблема

В Четвертой проблеме мы имеем две выборки равного размера, k. Мы должны найти минимальное значение k, такое, что с вероятностью P > 1/2 по крайней мере одна из выборок в первом множестве имеет то же самое значение, что и выборка во втором множестве. Чтобы решить проблему, мы сначала находим соответствующую вероятность P. Затем мы задаем вероятность 1/2, чтобы найти минимальный размер выборки.

Вероятность

Мы решаем это с использованием стратегии, подобной той, которую мы использовали для первой проблемы.

Согласно первой проблеме, вероятность, что все выборки в первом множестве имеют значения, отличающиеся от значений первой выборки во втором множестве, - Q₁ = (1 - 1/N)^k.
Вероятность, что все выборки в первом множестве имеют значения, отличающиеся от первых и вторых выборок во втором множестве, - Q₂ = (1- 1/N) ^k x (1 - 1/N) ^k.
Мы продолжаем рассуждения, чтобы показать, что вероятность, что все выборки в первом множестве имеют значения, отличающиеся от любой выборки во втором множестве:
```
Q_k = (1-1/N)^kx (1-1/N)^kx ... x (1-1/N)^k -> Q_k = (1-1/N)^kkQ_k =  (1-1/N)^kk -> Q_k = e^-kk/N
```
Используя аппроксимацию 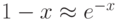$1 - x \approx e^{-x}$ при x = 1 / N
Наконец, если P - вероятность, что по крайней мере одна выборка из первого набора имеет то же самое значение, что и одна из выборок во втором наборе, то P = 1 - Q_k или имеем P = 1 - e^-kk/2N

Размер выборки

Теперь мы находим минимальный, общий размер выборок как это показано ниже:

P = 1 e^-kk/N >= 1/2 -> e^-kk/N<= 1/2 -> e^-kk/N<= 2
e^-kk/N<= ? -> e^-kk/N<= 2 -> k²/2N >= ln(2) -> k >= (2 x ln(2))^1/2 x N^1/2

Четвертая проблема

Вероятность: P = 1 e^-kk/N Размер выборки: k >= (ln(2))^1/2 x N^1/2

E.2. Итоги

Таблица E.1 дает выражения для вероятности ( P ) и размера выборки.( k ) для каждой из этих четырех проблем.

Таблица E.1. Итоги решений для четырех проблем дня рождения
Проблема	Вероятность	Общее выражение для k	Значение k при P >= 1/2
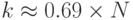
1	$P \approx e-k/N$	$k \approx ln[1/(1 - P)] \times N$	$k \approx 0.69 \times N$
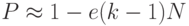
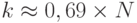
2	$P \approx 1 - e(k-1)N$	$k \approx ln[1/(1 - P)] \times N+1$	$k \approx 0,69 \times N$
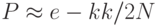
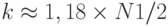
3	$P \approx e-kk/2N$	$k \approx [2ln(1/(1- P)]1/2 \times N1/2$	$k \approx 1,18 \times N1/2$
4	$P \approx e-kk/N$	$k \approx [ln[(1/(1 - P)]1/2 \times N1/2$	$k \approx 0,83 \times N1/2$