| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Конечные автоматы
2.2. Конфигурация конечного автомата
Определение 2.2.1. Конфигурацией
или мгновенным описанием (instantaneous description)
конечного автомата  называется любая упорядоченная пара
называется любая упорядоченная пара 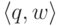 ,
где
,
где 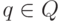 и
и 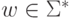 .
.
Замечание 2.2.2.
Содержательно конфигурация
представляет собой "мгновенное описание" конечного автомата.
Если представить, что исходное слово,
принадлежность которого рассматриваемому языку надо проверить,
дано в некотором "входном потоке",
то в конфигурации 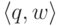 слово w
есть та часть исходного слова,
которая пока осталась во входном потоке
(это некоторый суффикс исходного слова),
а q -
текущее состояние "управляющего устройства".
слово w
есть та часть исходного слова,
которая пока осталась во входном потоке
(это некоторый суффикс исходного слова),
а q -
текущее состояние "управляющего устройства".
Определение 2.2.3.
Определим на множестве всех конфигураций конечного автомата M
бинарное отношение 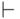 ( такт работы
(step)) следующим образом.
Если
( такт работы
(step)) следующим образом.
Если 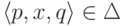 и
и 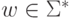 ,
то
,
то  .
Иногда вместо
.
Иногда вместо 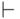 пишут
пишут  .
.
Пример 2.2.4. Рассмотрим конечный автомат
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{aaa}
\ar `ur_r{+/u7mm/}`r_dr{[0,2]}^{ab} "1,3"
\ar "1,3" ^{b}
&
& *=[o][F=]{2}
\ar `dl_l{+/d7mm/}`l_ul{[0,-2]}^{\varepsilon} "1,1"
}](/sites/default/files/tex_cache/e74bf3e36e22ef944fb5cb8f08ab3169.png)
 .
.Определение 2.2.5.
Бинарное отношение 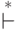 определяется как рефлексивное, транзитивное замыкание
отношения
определяется как рефлексивное, транзитивное замыкание
отношения 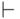 .
.
Пример 2.2.6.
Для конечного автомата из примера 2.1.2
выполняется 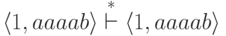 и
и  .
.
Лемма 2.2.7. Пусть дан конечный автомат 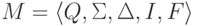 .
Слово
.
Слово 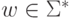 принадлежит языку L(M)
тогда и только тогда, когда
для некоторых
принадлежит языку L(M)
тогда и только тогда, когда
для некоторых  и
и  верно
верно 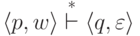 .
.
Лемма 2.2.8.
Если  и
и  ,
то
,
то 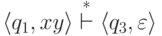 .
.
Доказательство.
Лемму легко доказать индукцией
по количеству тактов в вычислительном процессе,
ведущем из конфигурации 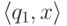 в конфигурацию
в конфигурацию 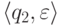 .
.
Упражнение 2.2.9. Рассмотрим конечный автомат.
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a}
\rloop{0,-1} ^{b}
\ar "1,2" ^{a}
& *=[o][F-]{2}
\ar "1,3" ^{b}
& *=[o][F=]{3}
}](/sites/default/files/tex_cache/a9d5e9fb82e39214b8627cc613b269c8.png)
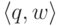 ,
удовлетворяющие условию
,
удовлетворяющие условию  .
.Упражнение 2.2.10.
Существуют ли конечный автомат M,
состояния q1, q2
и слова x, y, z,
такие что 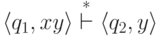 и
и 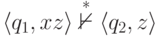 ?
?
Упражнение 2.2.11. Как связаны |Q|, 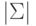 ,
,  , |w|
и число достижимых из
, |w|
и число достижимых из 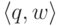 (в смысле
(в смысле 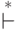 )
конфигураций?
)
конфигураций?
2.3. Конечные автоматы с однобуквенными переходами
Лемма 2.3.1. Каждый автоматный язык распознается некоторым конечным автоматом, не содержащим переходов с метками длины больше единицы и имеющим ровно одно начальное состояние и ровно одно заключительное состояние.
Пример 2.3.2.
Рассмотрим язык, заданный конечным автоматом  ,
где Q = {1,2},
,
где Q = {1,2},  , I = {1,2}, F = {1,2},
, I = {1,2}, F = {1,2},
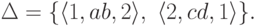
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
%
& *=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\ar `dr_dl{[2,0]}_{ab} "3,2"
&
\\
%
&
&
\\
%
& *=[o][F=]{2}
\ar @`{+/l16mm/} [] ^{}
\ar `ul_ur{[-2,0]}_{cd} "1,2"
&
}](/sites/default/files/tex_cache/3de670175e7f8bd8a4f6d95a0f9fa919.png)
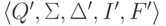 ,
где Q' = {0,1,2,3,4,5}, I' = {0}, F' = {5},
,
где Q' = {0,1,2,3,4,5}, I' = {0}, F' = {5},
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
%
&
& *=[o][F-]{1}
\ar "2,4" _{a}
\ar "2,5" ^{\varepsilon}
&
&
\\
*=[o][F-]{0}
\ar @`{+/l16mm/} [] ^{}
\ar "1,3" ^{\varepsilon}
\ar "3,3" _{\varepsilon}
& *=[o][F-]{4}
\ar "1,3" _{d}
&
& *=[o][F-]{3}
\ar "3,3" _{b}
& *=[o][F=]{5}
\\
%
&
& *=[o][F-]{2}
\ar "2,2" _{c}
\ar "2,5" _{\varepsilon}
&
&
}](/sites/default/files/tex_cache/1651ae38913fdc882b85cad830962275.png)
 и следующие два перехода заменяют старый переход
и следующие два перехода заменяют старый переход 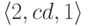 .
Чтобы обеспечить единственность начального состояния,
добавлены переходы
.
Чтобы обеспечить единственность начального состояния,
добавлены переходы  и
и  .
Последние два перехода в
.
Последние два перехода в 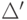 обеспечивают единственность заключительного состояния.
обеспечивают единственность заключительного состояния.Лемма 2.3.3. Каждый автоматный язык распознается некоторым конечным автоматом, содержащим только переходы с метками длины единица и имеющим ровно одно начальное состояние.
Доказательство.
Согласно лемме 2.3.1
можно предположить,
что исходный язык задан конечным автоматом  ,
не содержащим переходов с метками длины больше единицы,
причем |I| = 1.
Построим искомый конечный автомат
,
не содержащим переходов с метками длины больше единицы,
причем |I| = 1.
Построим искомый конечный автомат 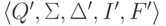 ,
положив Q' = Q, I' = I,
,
положив Q' = Q, I' = I,
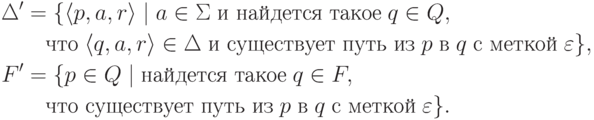
Пример 2.3.4.
Пусть 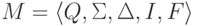 ,
где Q = {1,2,3},
,
где Q = {1,2,3},  , I = {1}, F = {3},
, I = {1}, F = {3},
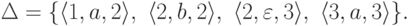
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" ^{a}
& *=[o][F-]{2}
\rloop{0,1} ^{b}
\ar "1,3" ^{\varepsilon}
& *=[o][F=]{3}
\rloop{0,1} ^{a}
}](/sites/default/files/tex_cache/599492e3931e7968074df9bc0a115a2d.png)
 .
Тот же язык распознается конечным автоматом
.
Тот же язык распознается конечным автоматом  ,
где F' = {2,3}
и
,
где F' = {2,3}
и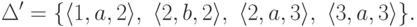
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" ^{a}
& *=[o][F=]{2}
\rloop{0,1} ^{b}
\ar "1,3" ^{a}
& *=[o][F=]{3}
\rloop{0,1} ^{a}
}](/sites/default/files/tex_cache/75e7138ea5f564a52819a8868759c079.png)
Упражнение 2.3.5. Найти конечный автомат с однобуквенными переходами,
распознающий язык 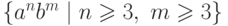
Упражнение 2.3.6. Найти конечный автомат с однобуквенными переходами,
распознающий язык 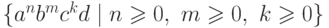
Упражнение 2.3.7. Существуют ли автоматный язык, который не распознается никаким конечным автоматом, содержащим только переходы с метками длины единица и имеющим ровно одно начальное состояние и ровно одно заключительное состояние?
