| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Слова, языки и грамматики
В начале этой лекции определяются основные понятия, используемые в дальнейшем: алфавит, слово, язык над данным алфавитом - и вводятся обозначения для пустого слова, конкатенации слов, степени слова, длины слова, количества вхождений данного символа. В разделе 1.2 фиксируются обозначения для префикса и суффикса слова, а также для ряда операций над языками, таких как конкатенация, итерация, обращение. При беглом чтении раздел 1.3, где определяются образ и полный прообраз языка при гомоморфизме, можно пропустить: вводимые в этом разделе понятия понадобятся только в лекциях "4" , "11" и "13" .
Используемые в приложениях формальные языки, как правило, являются бесконечными. Очевидно, нужен способ конечного описания формального языка. В данном курсе изучаются несколько классических средств: порождающие грамматики, автоматы, регулярные выражения. Определению понятий грамматики и порождаемого ею языка посвящен раздел 1.4. В конце первой лекции вводятся классы грамматик, образующие иерархию Хомского: грамматики типа 0 (все порождающие грамматики), грамматики типа 1 (контекстные грамматики), грамматики типа 2 (контекстно-свободные, или бесконтекстные, грамматики), грамматики типа 3 (праволинейные грамматики), а также менее важный класс линейных грамматик, промежуточный между классами грамматик типа 2 и 3.
Следует заметить, что каждая грамматика порождает ровно один язык, но обратное неверно: некоторые формальные языки нельзя задать никакой порождающей грамматикой, а каждому языку, который порождается хотя бы одной грамматикой, соответствует сразу бесконечное множество грамматик (причем они могут принадлежать разным классам).
1.1. Формальные языки
Определение 1.1.1. Будем называть натуральными числами неотрицательные целые числа. Множество всех натуральных чисел {0, 1, 2, ...} обозначается N.
Определение 1.1.2. Алфавитом называется конечное непустое множество. Его элементы называются символами ( буквами ).
Определение 1.1.3. Словом
( цепочкой, строкой, string)
в алфавите  называется конечная последовательность элементов
называется конечная последовательность элементов  .
.
Пример 1.1.4. Рассмотрим алфавит  = {a, b, c}.
Тогда baaa
является словом в алфавите
= {a, b, c}.
Тогда baaa
является словом в алфавите  .
.
Определение 1.1.5.
Слово, не содержащее ни одного символа
(то есть последовательность длины 0 ),
называется пустым словом
и обозначается  .
.
Определение 1.1.6.
Множество всех слов в алфавите  обозначается
обозначается 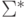 .
.
Замечание 1.1.7.
Множество  счетно.
В самом деле, в алфавите
счетно.
В самом деле, в алфавите  множество всех слов данной длины конечно,
следовательно,
множество всех слов данной длины конечно,
следовательно, 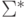 является объединением счетного числа конечных множеств.
является объединением счетного числа конечных множеств.
Определение 1.1.8.
Множество всех непустых слов в алфавите  обозначается
обозначается 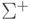 .
.
Пример 1.1.9.
Если  = {a},
то
= {a},
то 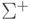 = {a,aa,aaa,aaaa,...}.
= {a,aa,aaa,aaaa,...}.
Определение 1.1.10.
Если  ,
то L называется языком
(или формальным языком )
над алфавитом
,
то L называется языком
(или формальным языком )
над алфавитом  .
.
Поскольку каждый язык является множеством,
можно рассматривать операции
объединения, пересечения и разности языков,
заданных над одним и тем же алфавитом
(обозначения  ).
).
Пример 1.1.11. Множество {a, abb} является языком над алфавитом {a, b}.
Определение 1.1.12.
Пусть  .
Тогда язык
.
Тогда язык  называется дополнением языка L
относительно алфавита
называется дополнением языка L
относительно алфавита  .
Когда из контекста ясно, о каком алфавите идет речь,
говорят просто, что язык
.
Когда из контекста ясно, о каком алфавите идет речь,
говорят просто, что язык  является дополнением
языка L.
является дополнением
языка L.
Определение 1.1.13.
Если x и y -
слова в алфавите  ,
то слово xy
(результат приписывания слова y в конец слова x )
называется конкатенацией,( катенацией, сцеплением )
слов x и y.
Иногда конкатенацию
слов x и y
обозначают
,
то слово xy
(результат приписывания слова y в конец слова x )
называется конкатенацией,( катенацией, сцеплением )
слов x и y.
Иногда конкатенацию
слов x и y
обозначают 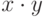 .
.
Определение 1.1.14.
Если x -
слово и 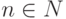 ,
то через xn
обозначается слово
,
то через xn
обозначается слово  .
Положим
.
Положим 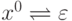 (знак
(знак 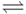 читается "равно по определению").
Всюду далее показатели над словами и символами,
как правило, являются натуральными числами.
читается "равно по определению").
Всюду далее показатели над словами и символами,
как правило, являются натуральными числами.
Пример 1.1.15. По принятым соглашениям ba3 = baaa и (ba)3 = bababa.
Пример 1.1.16.
Множество 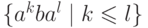 является языком над алфавитом {a,b}.
Этот язык содержит слова b, ba, aba, baa, abaa, baaa, aabaa, abaaa, baaaa
и т. д.
является языком над алфавитом {a,b}.
Этот язык содержит слова b, ba, aba, baa, abaa, baaa, aabaa, abaaa, baaaa
и т. д.
Определение 1.1.17. Длина слова w, обозначаемая |w|, есть число символов в w, причем каждый символ считается столько раз, сколько раз он встречается в w.
Пример 1.1.18. Очевидно,
что |baaa| = 4
и 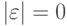 .
.
Определение 1.1.19. Через |w|a обозначается количество вхождений символа a в слово w.
Пример 1.1.20.
Если 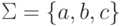 ,
то |baaa|a = 3, |baaa|b = 1
и |baaa|c = 0.
,
то |baaa|a = 3, |baaa|b = 1
и |baaa|c = 0.
Упражнение 1.1.21. Перечислить слова языка 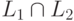 ,
где
,
где 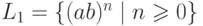 и
и 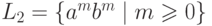 .
.
Упражнение 1.1.22. Пусть 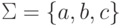 .
Равны ли языки
.
Равны ли языки 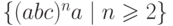 и
и 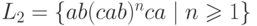 ?
?
Упражнение 1.1.23. Пусть 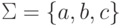 ,
, 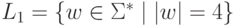 и
и 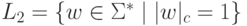 .
Сколько слов содержит язык L1 - L2?
.
Сколько слов содержит язык L1 - L2?
Упражнение 1.1.24. Пусть даны такие алфавиты 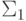 и
и  ,
что
,
что 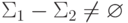 .
В каком случае
.
В каком случае  ?
?
