| ВКР |
Преподаватель
Вы можете этот курс.
Опубликован: 01.09.2008 | Уровень: для всех | Доступ: платный
Лекция 9:
Обоснование инвестиционных решений в условиях определенности
9.6. Критерии оценки экономической эффективности инвестиционных решений
Содержание всех пяти предыдущих параграфов данной лекции было подчинено обоснованию одной простой идеи: единственным критерием экономической эффективности инвестиционных проектов является чистая приведенная стоимость (NPV) денежных потоков по этим проектам. На этом однозначном утверждении базируется вся финансовая теория. Тем не менее, в практике инвестиционного проектирования используется значительно более широкий набор показателей эффективности инвестиций. Столь очевидное отступление от основополагающей истины нельзя списать лишь на недостаточное усвоение финансистами-практиками фундаментальных концепций теории финансов. Проблема заключается в невозможности точного измерения величины NPV. Абсолютно безупречный с теоретической точки зрения, данный параметр представляет собой некую абстрактную категорию (подобно понятию точки или линии в математике либо "абсолютного газа" в физике), не встречающуюся в реальной жизни в "чистом" виде. Казалось бы, не составляет никакого труда построить линию на листе бумаги. Однако, сколько бы мы ни прилагали старания к затачиванию карандаша, у нас никогда не получится "длина без ширины", как того требует теория.
Чистая приведенная стоимость ориентируется на будущие денежные потоки, и отсюда вытекают все трудности с практическим измерением ее величины. Формула расчета NPV безукоризненна, чего не скажешь о фактических числовых значениях, подставляемых в нее в ходе обоснования конкретных инвестиционных проектов. Нам пришлось сделать абсолютно нереалистичное предположение о полной определенности будущего только для того, чтобы в полной мере оценить простоту и изящество концепции чистой приведенной стоимости. Но у бизнесменов несколько иные цели и вряд ли их сможет заинтересовать какой-либо метод экономических расчетов только вследствие его теоретического изящества. Поэтому на практике достаточно широко применяются иные критерии оценки экономической эффективности инвестиций, которые, в конечном итоге, также не противоречат (точнее, не совсем противоречат) фундаментальному доходно-расходному принципу, но реализуют его в несколько иных, технически более простых формах. Как мы увидим впоследствии, каждый из этих "упрощенных" критериев страдает серьезными недостатками и все они значительно хуже критерия NPV, тем не менее широкое практическое распространение данных подходов обусловливает необходимость ознакомления с ними и понимания их сути.
Следует сразу оговориться, что в плане точности измерения, все эти суррогатные показатели ничуть не надежнее NPV, поэтому в последующих лекциях мы практически не будем к ним возвращаться. Если и затрачивать время и силы на более точное измерение какого-либо явления, то делать это лучше в отношении теоретически обоснованного параметра, а не случайного показателя, понравившегося только вследствие его кажущейся простоты и понятности. Здесь опять напрашивается аналогия с техническими измерениями: к примеру, вместимость железнодорожной цистерны можно обозначить в тоннах (40-тонная или 60-тонная цистерна). Но это плохой показатель вместимости, он не учитывает плотности вещества, которое будет заливаться в цистерну. Если кому-нибудь взбредет в голову измерить вместимость данного транспортного средства более точно, то лучше будет воспользоваться мерами объема (кубическими метрами или литрами), которые более адекватно отражают величину интересующего параметра. В экономических измерениях (в том числе и в инвестиционных расчетах) искомым параметром в конечном счете всегда выступает стоимость, поэтому следует прилагать усилия к уточнению измерения показателя, наиболее релевантного именно для этого параметра (а таковым, безусловно, является NPV), а не растрачиваться на изобретение хитроумных методик измерения площади в граммах или массы в секундах.
Наглядной иллюстрацией нестандартного подхода к использованию единиц измерения в экономических расчетах является один из наиболее популярных на практике показателей экономической эффективности инвестиций – срок окупаемости проектов (Pay-Back Period, PB). В данном случае для измерения стоимости используются единицы измерения времени – годы реализации проекта. Можно предположить, что теоретическим обоснованием для применения данного измерителя служит нестареющее правило бизнеса: "Время это деньги". Чем больше времени требуется для того, чтобы возвратить (или "отбить" в современной терминологии) инвестированные в проект деньги, тем хуже проект. И наоборот, хорошие проекты позволяют быстрее возвращать вложенные в них деньги, то есть, экономят бизнесменам время, которое для последних – те же деньги.
Для расчета величины этого показателя прогнозируемые годовые значения свободных денежных потоков по проекту ( 
) суммируются до тех пор, пока их накопленная сумма не станет равной 0 (сумма положительных притоков, генерируемых проектом, начиная с года 1, сравняется с объемом первоначальных инвестиций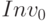 
в проект). Номер года 
, в котором достигается строгое равенство 
, и принимается в качестве фактического значения показателя 
проекта. Если точное определение периода затруднено вследствие того, что накопленная величина 
меньше суммы инвестиций, а при 
уже превышает эту сумму, то выполняется условный расчет дробной части показателя – доли года 
, необходимой для полного покрытия дефицита денежных средств, остающегося к концу периода 
. Рассмотрим методику расчета срока окупаемости проекта на конкретном сквозном примере (табл. 9.13).
Для обоих способов начисления амортизации первоначальные инвестиции полностью погашаются в течение 4-го года проекта (j = 4). Однако нам неизвестно, когда именно в течение данного года (в его начале, конце середине и т.д.) будет покрыт денежный дефицит, переходящий с предыдущего года ( j – 1 = 3). Для варианта с 20%-м начислением амортизации сумма этого дефицита к концу 3-го года составит 14,28 млн. руб., а при начислении амортизации по ставке 10% дефицит равен 17,16 млн. руб.
Остановимся более подробно на первом варианте (амортизационные отчисления по ставке 20%). FCF за 4-й год при этом варианте составляет 18,4 млн. руб. Для покрытия дефицита (14,28 млн. руб.) достаточно лишь 77,61% этой годовой величины (14,28 / 18,4 * 100). Таким образом, для полного возврата первоначальных инвестиций, понадобится 3 полных года реализации проекта плюс 0,78 четвертого года. Следовательно, срок окупаемости проекта ( 
) равен 3,78 года. Аналогичным образом рассчитаем 
.
Недостатки показателя PB, что называется, бросаются в глаза: он не учитывает денежных потоков, остающихся за пределами срока окупаемости; для его расчета используются недисконтированные значения FCF; при его использовании преимущество отдается краткосрочным проектам, что может ослабить внимание к долгосрочной стратегии развития предприятия. Однако, за всеми этими (и другими) недостатками не стоит терять из виду важное преимущество этого показателя – на интуитивном уровне он "ухватывает" принципиальную связь, существующую между процессом формирования стоимости и временем. Очевидно, что по мере удлинения срока проекта увеличиваются связанные с этим проектом риски (неопределенность будущих результатов). Поэтому преимущество быстроокупаемых проектов заключается не только (и не столько) в их высокой доходности (интенсивности генерирования денежных потоков), но и в относительно менее высоком уровне их риска в сравнении с более длительными инвестициями. Расчет срока окупаемости позволяет достаточно быстро и без использования сложного математического аппарата осуществить первичную (и конечно же, очень грубую) оценку возможных рисков проекта.
Еще одно интересное свойство показателя срока окупаемости наглядно иллюстрируется результатами выполненных нами расчетов. Фактическое значение 
оказалось заметно ниже величины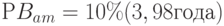 
. То есть, несмотря на то что в явном виде процедура дисконтирования денежных потоков при расчете этих показателей не осуществлялась, они уловили различия, возникающие в результате влияния эффекта "налоговой защиты" по амортизационным отчислениям. Проект с 20%-м начислением амортизации выглядит более предпочтительным, так как он обеспечивает получение более высоких денежных потоков в первые годы реализации. Эта экономия полностью компенсируется на 5-м году реализации проекта с начислением амортизации по ставке 10%, однако, с учетом временной стоимости денег, преимущество все равно остается за первым вариантом. Показатель PB демонстрирует это преимущество, хотя по формальным признакам, временная стоимость денег при его расчете не учитывалась.
Строго говоря, ничто не мешает рассчитать срок окупаемости проекта с учетом дисконтированных денежных потоков, и данная методика получила достаточно широкое распространение. Рассмотрим ее на примере наших сквозных данных, представленных в табл. 9.14.
Срок окупаемости по первому варианту ( 
) составит 4,06 года (4 + 2,65 / 40,84). По второму варианту ( 
) он также будет несколько выше: 4,14 года (4 + 6,05 / 43,85). В целом, для обоих способов начисления амортизации, оценка выглядит более консервативной, однако различия между первым и вторым вариантами уже не столь заметны. Можно сказать, что те небольшие преимущества, которые все-таки есть у показателя срока окупаемости, отнюдь не усиливаются в результате его расчета на базе дисконтированных денежных потоков. Кроме этого, расчет дисконтированного срока окупаемости, по сути дела, повторяет расчет чистой приведенной стоимости, поэтому может возникнуть вопрос о целесообразности дальнейшего "усовершенствования" методики вычисления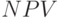 
.
Следующий "нетрадиционный" критерий экономической эффективности перекочевал в финансовый менеджмент из бухгалтерского учета. В этом смысле он является более чем "традиционным", так как, по сути дела, копирует широко распространенный в анализе финансовой отчетности показатель рентабельности активов (точнее, рентабельности инвестированного капитала – ROCE). "Бухгалтерские" корни данного критерия нашли отражение в его названии: учетная доходность или среднегодовая учетная доходность (Accounting Rate of Return – ARR или Average Accounting Return – AAR). Основная проблема с использованием данного показателя характерна для всего бухгалтерского учета в целом: при кажущейся строгости и однозначности бухгалтерских терминов (особенно таких как "дебет", "кредит", "сальдо" или даже "крыжить"!) в методах их количественного измерения царит сущий произвол и субъективизм. Даже вооруженный самыми совершенными учетными стандартами и находящийся под контролем самых авторитетных и сертифицированных аудиторов, скромный бухгалтер умудряется настолько творчески переработать поступающую к нему информацию, что попытка последующего точного воспроизведения полученных им результатов, как правило, заканчивается полным провалом. Не случайно, две авторитетнейшие в финансово-учетной сфере компании – S&P и PWC – до сих пор никак не могут решить, кто же из них более правильно определяет "истинную" величину операционной прибыли по финансовым отчетам компаний, входящих в индекс S&P 500.
Общий подход к расчету ARR прост и однозначен – среднегодовую сумму бухгалтерской чистой прибыли по проекту следует разделить на среднегодовую учетную стоимость активов по этому же проекту. Трудности возникают при определении фактических значений показателей, используемых для расчета. Как уже неоднократно отмечалось в данной лекции, целью инвестиционного проектирования является отнюдь не составление бухгалтерской отчетности по проекту (что невозможно сделать в принципе, так как при обосновании инвестиций учитываются только будущие денежные потоки, в то время как бухгалтерия ориентируется на фактические, то есть, прошлые данные). Прогнозные финансовые отчеты по всем своим ключевым параметрам отличаются от своих бухгалтерских аналогов. Поэтому, достаточно сложно определить величину бухгалтерской чистой прибыли по проекту. Отраженный в прогнозном отчете о прибылях и убытках показатель чистой прибыли включает в себя доход от переоценки по рыночной стоимости активов, остающихся к моменту окончания проекта. Поэтому данный показатель не может рассматриваться как "учетный". Точно так же, не является "учетной" сама терминальная стоимость остающихся активов, отраженная в прогнозном балансе проекта на конец последнего года.
Во избежание возможных разночтений и несогласованностей, наиболее часто рекомендуется следующий вариант расчета: суммы чистой прибыли за каждый год реализации проекта определяются путем добавления к величине годового OCF величины начисленной за год амортизации. Затем производится усреднение полученных годовых сумм (по формуле средней арифметической простой). Знаменатель формулы расчета ARR определяется путем деления пополам суммы первоначальных инвестиций в проект ( 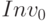) и остаточной (учетной) стоимости долгосрочных активов на момент завершения проекта. Остаточная величина NWC на конец года n принимается равной 0, то есть, не учитывается в ходе вычислений.
