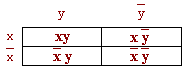Метод проб

Минимизирующие диаграммы

Этот метод графической минимизации был изложен Карно, который ввел в употребление специальные карты. Эти карты позволяют для функции, зависящей от небольшого числа аргументов (до пяти - шести) находить результаты всех возможных склеек. Карты впоследствии были усовершенствованы Вейчем, а сам метод иногда именуется как метод минимизации с помощью диаграмм Вейча.

Рассмотрим существо способа для функций, зависящих от 2, 3 и 4-х переменных.

Функции 2-х переменных

Диаграмма – матрица, столбцам и строкам которой приписывается смысл переменных, входящих в функцию в прямом или инверсном виде.

В клетках матрицы ставится произведение, образованное из букв, которыми названы строки и столбцы матрицы.

Обратим внимание на то, что данная матрица сразу указывает на возможную склейку произведений, входящих в выражение функции.

Так склейке подлежат все произведения, расположенные в соседних по вертикали и горизонтали клетках.

• xy склеивается с xy и с xy ;
• xy склеивается с xy и с xy ;
• xy склеивается с xy и с xy ;
• xy склеивается с xy и с xy ;

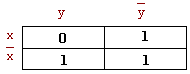
Более того, эта же диаграмма дает и результат склейки: это название или строки, или столбца. При минимизации по данному методу заполняется диаграмма функции 2-х переменных по следующему правилу: если то или иное произведение входит в СДНФ функции, то в соответствующую ему клетку диаграммы ставится единица, и нуль – в противном случае. Если в диаграмме находится хотя бы две соседние единицы, то это означает, что два произведения склеиваются, а результатом склейки является произведение (в данном случае из одной буквы), именем которого названа данная строка или столбец.

Пример:

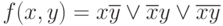
Выделим в диаграмме соседние единицы, и результат склейки дает минимальную форму функции: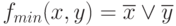

Заметим, что результатом склейки является результат покрытия конституент единицы исходной функции простыми импликантами. В данном случае переменными, которыми названы строки и столбцы диаграммы.

Функции 3-х переменных

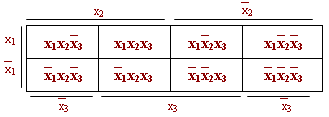
Для минимизации функций, зависящих от трех переменных, применяется следующая диаграмма:

Из диаграммы видно, что склейке подлежат все произведения, расположенные в соседних клетках, а также в клетках, расположенных на краях диаграммы. Результат склейки – есть произведения, содержащее на одну букву меньше. Видно также, что возможна и дальнейшая склейка, однако уже между произведениями, расположенными во взаимно перпендикулярном направлении.

Рассмотрим, например, левую половину диаграммы:

Склеим попарно произведения, стоящие в строках:

Теперь видим, что можно произвести дальшейшую склейку, но произведений, стоящих в столбцах матрицы:

Как видно, результат склейки – произведение x₂. Именно эта переменная покрывает все четыре конституенты единицы СДНФ функции.

Подобное же утверждение справедливо и для конституент, расположенных в строках и столбцах диаграммы по краям таблицы.

Таким образом, при поиске минимальной формы необходимо считать левый край таблицы склеенным с правым. Говорят, что для наглядности можно условно данную диаграмму представить нанесенной на поверхность цилиндра.

Пример:

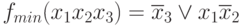
Видим, что две единицы, соответствующие конституентам x₁x₂x₃ и x₁x₂x₃, покрываются произведением x₁x₂.