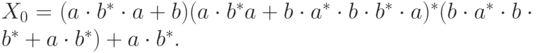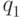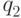|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Формальные языки
Для регулярного выражения  , где
, где  и
и  — регулярные выражения, можно построить задающий
автомат
— регулярные выражения, можно построить задающий
автомат 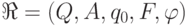 следующим образом. Пусть автомат
следующим образом. Пусть автомат  задает
задает  , а автомат
, а автомат  задает
задает  . Не уменьшая общности, опять считаем, что
. Не уменьшая общности, опять считаем, что  и
и 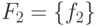 — одноэлементные и что
— одноэлементные и что 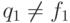 ,
,  . Положим
. Положим 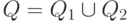 и поясним
построение автомата
и поясним
построение автомата  на языке диаграмм. Финальное состояние
автомата
на языке диаграмм. Финальное состояние
автомата  соединим дугой со стартовым состоянием
автомата
соединим дугой со стартовым состоянием
автомата  и пометим ее символом
и пометим ее символом  .
В качестве
.
В качестве  возьмем стартовое состояние
автомата
возьмем стартовое состояние
автомата  , а в качестве финального
состояния
, а в качестве финального
состояния  возьмем финальное состояние
возьмем финальное состояние  автомата
автомата  .
.
Для регулярного выражения  , где
, где  —
регулярное выражение, можно построить задающий автомат
—
регулярное выражение, можно построить задающий автомат  следующим образом.
Пусть автомат
следующим образом.
Пусть автомат 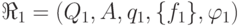 задает
задает  . Опять не уменьшая
общности, считаем, что
. Опять не уменьшая
общности, считаем, что  — одноэлементное
и что
— одноэлементное
и что  . Добавляем к множеству
. Добавляем к множеству 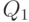 два
новых состояния —
два
новых состояния —  и
и  . Соединяем
. Соединяем  -переходами пары
состояний
-переходами пары
состояний  ,
, 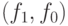 ,
,  и
и  .
.
В завершение заметим, что изложенные приемы, очевидно, позволяют по любому
регулярному выражению  построить недетерминированный автомат
построить недетерминированный автомат  с
с  -переходами, с одним стартовым и одним финальным
состоянием, причем стартовое состояние отлично от финального, и при этом такой,
что
-переходами, с одним стартовым и одним финальным
состоянием, причем стартовое состояние отлично от финального, и при этом такой,
что  .
.
Таким образом, задача синтеза решена.
Избавление от  -переходов.
Покажем, как по недетерминированному автомату
-переходов.
Покажем, как по недетерминированному автомату 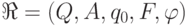 с
с  -переходами построить недетерминированный
автомат
-переходами построить недетерминированный
автомат  ) без
) без  -переходов,
такой, что
-переходов,
такой, что 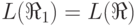 . Назовем
. Назовем  -путем путь
в диаграмме автомата
-путем путь
в диаграмме автомата  , возможно пустой, порождающий пустое
слово. Обозначим через
, возможно пустой, порождающий пустое
слово. Обозначим через  множество состояний, достижимых из
множество состояний, достижимых из  с помощью некоторого
с помощью некоторого  -пути.
-пути.
Положим  .
Переходную функцию
.
Переходную функцию 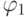 построим следующим образом
построим следующим образом
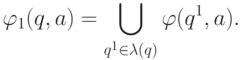
Детерминизация.Покажем, как по недетерминированному автомату 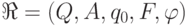 без
без  -переходов построить
детерминированный автомат
-переходов построить
детерминированный автомат  ,
такой, что
,
такой, что 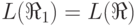 . Положим
. Положим  ,
,  ,
, 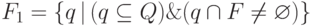 , а
, а  определим следующим образом:
определим следующим образом:
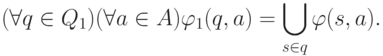
 удовлетворяет условию
удовлетворяет условию 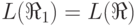 .
.Анализ. Для завершения доказательства теоремы покажем, как по
заданному детерминированному конечному автомату ( построить регулярное
выражение  , такое, что
, такое, что  . Именно это
и называют задачей анализа. Правда, метод, который мы используем, можно
применить и к недетерминированным автоматам. Метод заключается в том, что
мы сводим задачу к решению стандартной системы уравнений. Итак, рассмотрим
автомат
. Именно это
и называют задачей анализа. Правда, метод, который мы используем, можно
применить и к недетерминированным автоматам. Метод заключается в том, что
мы сводим задачу к решению стандартной системы уравнений. Итак, рассмотрим
автомат 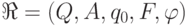 .
.
Пусть  ,
, 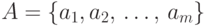 .
Введем переменные
.
Введем переменные 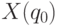 ,
,  .
Переменную
.
Переменную 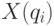 для каждого
для каждого  будем
интерпретировать как множество слов, которые можно прочитать, начиная
от состояния
будем
интерпретировать как множество слов, которые можно прочитать, начиная
от состояния  и заканчивая в финальном состоянии,
тогда
и заканчивая в финальном состоянии,
тогда 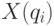 должна удовлетворять уравнению
должна удовлетворять уравнению
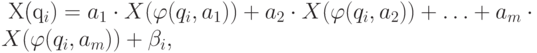
 , если
, если 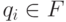 ,
,  ,
если
,
если  . Решив систему, берем в качестве ответа
значение
переменной
. Решив систему, берем в качестве ответа
значение
переменной 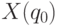 .
.Задача. Построить регулярное выражение в алфавите 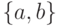 ,
задающее язык, порождаемый автоматом
,
задающее язык, порождаемый автоматом  ,
где
,
где  ,
,  ,
,  и переходная функция
и переходная функция  задана
таблицей
задана
таблицей
Решение. Запишем систему уравнений
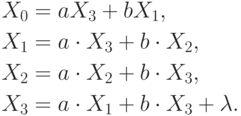
Из четвертого уравнения получаем 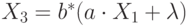 .
Подставляя полученное выражение во все остальные уравнения, получим
систему из трех уравнений:
.
Подставляя полученное выражение во все остальные уравнения, получим
систему из трех уравнений:

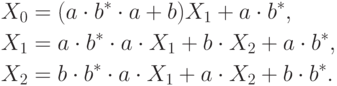
 и подставляем в остальные уравнения:
и подставляем в остальные уравнения: 
Преобразуем второе уравнение к стандартному виду
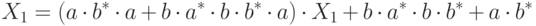
и получаем из него
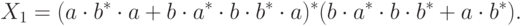
Наконец, получаем ответ