НОУ ИНТУИТ | Структуры данных и модели вычислений. Лекция 12: Абак, алгорифмы Маркова, равнодоступная адресная машина

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.09.2006 | Уровень: специалист | Доступ: свободно

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

Алгорифмы Маркова

Термин "алгорифм" является устаревшим вариантом современного термина "алгоритм", однако по отношению к алгоритмам Маркова принято использовать авторский вариант.

Информация, обрабатываемая алгорифмом Маркова, представляется словом в некотором фиксированном алфавите .

Алгорифм (программа) представляется последовательностью пар слов в алфавите . Пары, составляющие алгорифм, называются также подстановками и записываются в виде

$\eq*{ \al \to \beta, }$

где $\al$ , $\beta$ — слова в алфавите

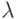, причем $\beta$ может быть пустым (обозначаем $\lm$ ). Программа имеет вид

$\begin{gather*} \al_1 \to \bt_1\\ \al_2 \to \bt_2\\ \mdots{2cm}\\ \al_i \to \bt_i!\\ \mdots{2cm}\\ \al_n \to \bt_n. \end{gather*}$

Некоторые подстановки помечаются восклицательным знаком и называются заключительными.

Функционирование. Во входном слове ищется фрагмент, совпадающий с левой частью первой подстановки. Если фрагмент находится, то самый левый такой фрагмент во входном слове заменяется на ее правую часть, в противном случае рассматривается вторая подстановка из алгорифма и так далее. Вычисления заканчиваются, когда ни одна из левых частей подстановок не является фрагментом обработанного к данному моменту слова или когда выполнена заключительная подстановка. Заметим, что описанный таким образом процесс может оказаться и бесконечным.

Замечание. Алгорифмы Маркова составляют теоретическую основу системы программирования, использующую язык РЕФАЛ.

Пример. Алфавит 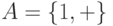$A = \{1, +\}$ . Здесь запятая не является символом алфавита.

Рассмотрим программу

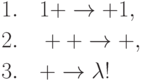
$\begin{align*} 1. &\q 1+ \to +1,\\ 2. &\q ++ \to +,\\ 3. &\q + \to \lm! \end{align*}$

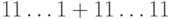Убедитесь в том, что она входное слово вида $11\ldots 1 + 11\ldots 11$ переработает в слово $11\ldots 1$ , в котором число символов "1" — такое же, как во входном слове. Можно считать, что программа выполняет сложение натуральных чисел, представленных в унарной системе счисления.

Пример. Алфавит $A = \{1, \ast, v, z\}$ .

Программа

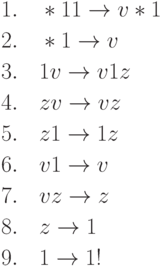
$\begin{align*} 1. &\q *11 \to v*1 \\ 2. &\q *1 \to v\\ 3. &\q 1v \to v1z\\ 4. &\q zv \to vz\\ 5. &\q z1 \to 1z\\ 6. &\q v1 \to v\\ 7. &\q vz \to z\\ 8. &\q z \to 1 \\ 9. &\q 1 \to 1! \end{align*}$

Рассмотрим протокол вычислений на входном слове $11\ast 111$ . Справа указаны применяемые подстановки.

$\begin{align*} & 11\ast 111 && \ast11 \to v \ast 1\\[-1pt] & 11v \ast 11 && \ast 11 \to v \ast 1\\[-1pt] & 11 vv\ast 1 && \ast 1 \to v\\[-1pt] & 11vvv && 1v \to v1z\\[-1pt] & 1v1zvv && 1v \to v1z\\[-1pt] & v1z1zvv && zv \to vz\\[-1pt] & v1z1vzv && 1v \to v1z\\[-1pt] & v1zv1zzv && zv \to vz\\[-1pt] & v1vz1zzv && 1v \to v1z\\[-1pt] & vv1zz1zzv && zv \to vz\\[-1pt] & vv1zz1zvz && zv \to vz\\[-1pt] & vv1zz1vzz && 1v \to v1z\\[-1pt] & vv1zzv1zzz && zv \to vz\\[-1pt] & vv1zvz1zzz && zv \to vz\\[-1pt] & vv1vzz1zzz && 1v \to v1z\\[-1pt] & vvv1zzz1zzz && z1 \to 1z\\[-1pt] & vvv1zz1zzzz && z1 \to 1z\\[-1pt] & vvv1z1zzzzz && z1 \to 1z\\[-1pt] & vvv11zzzzzz && v1 \to v\\[-1pt] & vvv1zzzzzz && v1 \to v\\[-1pt] & vvvzzzzzz && vz \to z\\[-1pt] & vvzzzzzz && vz \to z\\[-1pt] & vzzzzzz && vz \to z\\[-1pt] & zzzzzz && z \to 1\\[-1pt] & 1zzzzz && z \to 1\\[-1pt] & 11zzzz && z \to 1\\[-1pt] & 111zzz && z \to 1\\[-1pt] & 1111zz && z \to 1\\[-1pt] & 11111z && z \to 1\\[-1pt] & 111111 && 1 \to 1! \end{align*}$

Если считать, что во входном слове закодирована задача умножения $2\ast 3$ в унарной системе счисления, то в выходном слове получен ответ 6.

Докажите, что программа дает верный ответ при любом корректном входном слове.

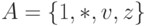Дальше >>

Авторизоваться

Структуры данных и модели вычислений

Абак, алгорифмы Маркова, равнодоступная адресная машина

Алгорифмы Маркова

Вопросы и ответы