|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Поисковые деревья
Случайные двоичные деревья поиска
Поскольку основные операции с двоичными деревьями поиска требуют
времени 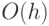 , где
, где  — высота дерева, важно
знать, какова высота "типичного" дерева. Для этого принимают какие-то статистические
предположения о распределении ключей и последовательности выполняемых
операций. К сожалению, в общем случае ситуация трудна для анализа. Если
определить случайное двоичное дерево из
— высота дерева, важно
знать, какова высота "типичного" дерева. Для этого принимают какие-то статистические
предположения о распределении ключей и последовательности выполняемых
операций. К сожалению, в общем случае ситуация трудна для анализа. Если
определить случайное двоичное дерево из  различных ключей как
дерево, получающееся из пустого дерева добавлением этих ключей в случайном
порядке, считая все
различных ключей как
дерево, получающееся из пустого дерева добавлением этих ключей в случайном
порядке, считая все  ! перестановок равновероятными, то можно
доказать, что средняя высота случайного двоичного дерева поиска,
построенного по
! перестановок равновероятными, то можно
доказать, что средняя высота случайного двоичного дерева поиска,
построенного по  различным ключам, равна
различным ключам, равна  .
.
Красно-черные деревья
Мы видели, что основные операции с двоичным поисковым деревом
высоты  могут быть выполнены за
могут быть выполнены за 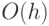 действий. Деревья
эффективны, если их высота мала, но если не принимать специальные меры при
выполнении операций, малая высота не гарантируется, и в этом случае
деревья не более эффективны, чем списки.
действий. Деревья
эффективны, если их высота мала, но если не принимать специальные меры при
выполнении операций, малая высота не гарантируется, и в этом случае
деревья не более эффективны, чем списки.
Для повышения эффективности операций используют различные приемы
перестройки деревьев, чтобы высота дерева была величиной  .
Такие приемы называются балансировкой деревьев. При этом используются
разные критерии качества балансировки. Одним из видов сбалансированных
деревьев поиска являются так называемые красно-черные деревья, для которых
предусмотрены операции балансировки, гарантирующие оценку высоты
величиной
.
Такие приемы называются балансировкой деревьев. При этом используются
разные критерии качества балансировки. Одним из видов сбалансированных
деревьев поиска являются так называемые красно-черные деревья, для которых
предусмотрены операции балансировки, гарантирующие оценку высоты
величиной  .
.
Частным случаем такой балансировки является АВЛ-балансировка, при которой
у каждого узла высота его левого поддерева отличается от высоты правого не
более чем на единицу. Заметим, что наихудшими в некотором смысле
АВЛ-деревьями являются деревья Фибоначчи 
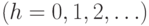 ,
определяемые следующим образом:
,
определяемые следующим образом: 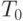 — пустое
дерево,
— пустое
дерево, 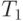 — дерево, состоящее из одного узла. При
— дерево, состоящее из одного узла. При 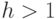 дерево
дерево  состоит из корня с левым
поддеревом
состоит из корня с левым
поддеревом 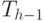 и правым —
и правым —  . Нетрудно
видеть, что при заданной величине
. Нетрудно
видеть, что при заданной величине  дерево
дерево  имеет
наименьшее число узлов среди всех АВЛ-деревьев
высоты
имеет
наименьшее число узлов среди всех АВЛ-деревьев
высоты  .
.
Для удобства поисковые деревья будем расширять, вводя дополнительный
фиктивный узел (  -узел)
и считая его потомком каждого узла исходного
дерева, у которого нет правого, левого или обоих потомков, его же считаем
родителем корня.
-узел)
и считая его потомком каждого узла исходного
дерева, у которого нет правого, левого или обоих потомков, его же считаем
родителем корня.
Красно-черное дерево — это расширенное двоичное дерево поиска, вершины которого разделены на красные (red) и черные (black) так, что:
- Каждый узел либо красный, либо черный.
- Каждый лист (
 -узел) — черный.
-узел) — черный. - Если узел красный, то оба его ребенка черные.
- Все пути, идущие вниз от корня к листьям, содержат одинаковое количество черных узлов.
Свойства 1-4 называют RB-свойствами. Узлы красно-черного дерева будем представлять записями вида
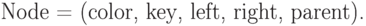
Комбинаторные свойства красно-черных деревьев
Для произвольного узла  определим черную
высоту
определим черную
высоту 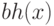 как количество черных узлов на пути из
как количество черных узлов на пути из  в некоторый
лист, не считая сам узел
в некоторый
лист, не считая сам узел  . По свойству 4 эта сумма не зависит от
выбранного листа. Черной высотой дерева будем считать черную высоту его корня.
. По свойству 4 эта сумма не зависит от
выбранного листа. Черной высотой дерева будем считать черную высоту его корня.
Пусть ![{\rm size}[x]](/sites/default/files/tex_cache/aa593d2da37d1e16c21a5ffb7cc44f24.png) — количество внутренних узлов в
поддереве с корнем
— количество внутренних узлов в
поддереве с корнем  (
(  -узлы не считаются).
-узлы не считаются).
Лемма 1.
Для произвольного узла  красно-черного дерева выполняется
неравенство
красно-черного дерева выполняется
неравенство ![{\rm size}[x] \ge 2^{bh(x)} - 1](/sites/default/files/tex_cache/c4292075026a8d352cf8c078b1619aaa.png) .
.
Доказательство.
Если  — лист, то
— лист, то 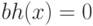 и
и ![{\rm size}[x]
= 0](/sites/default/files/tex_cache/15e51c9a179f59ed505d272b3597a279.png) ,
следовательно, утверждение леммы выполнено. Далее,
пусть для узлов
,
следовательно, утверждение леммы выполнено. Далее,
пусть для узлов ![{\rm left}[x]](/sites/default/files/tex_cache/53537fa398cfe9badf8049e2606f38dc.png) и
и ![{\rm
right}[x]](/sites/default/files/tex_cache/78db6cae66d3450a293a8538d1569851.png) утверждение леммы справедливо, то есть
утверждение леммы справедливо, то есть
![\eq*{
{\rm size} [{\rm left} [x]] \ge
2^{bh({\rm left} [x])}
- 1\ \t{и}\ {\rm size} [{\rm right}[x]] \ge 2^{bh({\rm right} [x])} - 1,
}](/sites/default/files/tex_cache/37634179899671747a40a3cc4d272101.png)
тогда
![\eq*{
\begin{gathered}
{\rm size} [x] = {\rm size} [{\rm left} [x]] + {\rm size}
[{\rm right} [x]] + 1 \ge \\
\ge (2^{bh({\rm left} [x])} - 1) + (2^{bh({\rm right}[x])} -1) + 1 = \\
= 2^{bh({\rm left}[x])}+2^{\rm bh({\rm right}[x])} - 1 \ge
2^{bh(x)-1} + 2^{bh(x)-1} - 1 \ge 2^{bh(x)} - 1.
\end{gathered}
}](/sites/default/files/tex_cache/430489f8b72887b76a44ac721aa18cf2.png)
Предпоследнее неравенство справедливо в силу соотношения
![\eq*{
bh({\rm left}[x]) \ge (bh(x) - 1)\ \t{и}\ bh({\rm right}[x]) \ge
(bh(x) - 1).
}](/sites/default/files/tex_cache/7fa05c11f61cc61ad6bfd3be48f55599.png)
Лемма 2.
Красно-черное дерево с  внутренними узлами
внутренними узлами  -листья не считаются
-листья не считаются 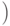 имеет высоту не
больше
имеет высоту не
больше 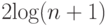 .
.
Доказательство.
Обозначим высоту дерева через  . Согласно
свойству 3, по меньшей мере половину всех вершин на пути от корня к листу,
не считая корень, составляют черные вершины. Следовательно, черная высота
дерева не меньше
. Согласно
свойству 3, по меньшей мере половину всех вершин на пути от корня к листу,
не считая корень, составляют черные вершины. Следовательно, черная высота
дерева не меньше  . Тогда
. Тогда  и,
переходя к логарифмам, получаем
и,
переходя к логарифмам, получаем 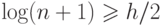 или
или  . Лемма доказана.
. Лемма доказана.
Полученная оценка высоты красно-черных деревьев гарантирует выполнение
операций  ,
,  ,
,  ,
,  и
и 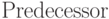 с красно-черными деревьями за
время
с красно-черными деревьями за
время  . Сложнее обстоит дело
с процедурами
. Сложнее обстоит дело
с процедурами  и
и  проблема в том, что они могут испортить структуру красно-черного дерева,
нарушив RB-свойства. Поэтому описанные процедуры придется модифицировать.
Ниже увидим, как можно реализовать их за время
проблема в том, что они могут испортить структуру красно-черного дерева,
нарушив RB-свойства. Поэтому описанные процедуры придется модифицировать.
Ниже увидим, как можно реализовать их за время  с сохранением RB-свойств.
с сохранением RB-свойств.
