|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Ленивые левосторонние и самоорганизующиеся кучи
Утверждение.
Время  выполнения
выполнения  операций СЛИТЬ,
примененных к коллекции, состоящей из
операций СЛИТЬ,
примененных к коллекции, состоящей из 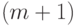 куч с нулевым
потенциалом, является величиной
куч с нулевым
потенциалом, является величиной 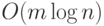 , где
, где  — общее количество узлов в коллекции.
— общее количество узлов в коллекции.
Доказательство.
Пусть  -я операция заключается в слиянии куч
-я операция заключается в слиянии куч  и
и 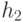 в результирующую кучу
в результирующую кучу  .
Пусть перед ее выполнением
.
Пусть перед ее выполнением  и
и  — количества тяжелых
узлов в правых путях куч
— количества тяжелых
узлов в правых путях куч  и
и 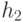 соответственно,
соответственно, 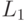 и
и 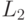 —
количества легких узлов в этих путях,
—
количества легких узлов в этих путях, 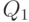 ,
, 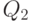 — количества тяжелых узлов в остальных частях куч.
— количества тяжелых узлов в остальных частях куч.
Время выполнения этой операции с точностью до постоянного множителя
оценивается сверху величиной 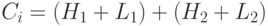 .
.
Подсчитаем изменение 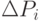 потенциала при ее выполнении.
Имеем
потенциала при ее выполнении.
Имеем

По завершении этой операции тяжелые узлы правых путей становятся легкими,
их количество равно  . Легкие узлы правых путей могут
как стать тяжелыми, так и остаться легкими, их будет
не более
. Легкие узлы правых путей могут
как стать тяжелыми, так и остаться легкими, их будет
не более  штук, а количества тяжелых узлов
в остальной части обоих деревьев
штук, а количества тяжелых узлов
в остальной части обоих деревьев  не изменились.
Следовательно, количество
не изменились.
Следовательно, количество  тяжелых узлов после выполнения операции удовлетворяет неравенству
тяжелых узлов после выполнения операции удовлетворяет неравенству
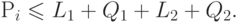
Таким образом, получаем изменение потенциала
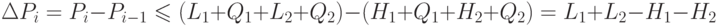
и, следовательно,
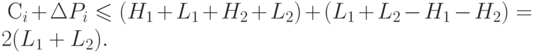
Из определения легкого узла следует, что количество 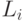 легких
узлов в куче
легких
узлов в куче 
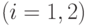 не превосходит логарифма
количества
не превосходит логарифма
количества 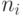 узлов в этой куче.
узлов в этой куче.
Следовательно,
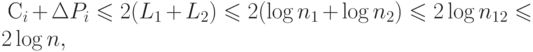
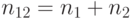 , а
, а  — общее количество
узлов
в исходных
— общее количество
узлов
в исходных  кучах.
кучах.Суммируя левую и правую части последнего неравенства
по 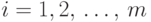 , получаем, что величина
, получаем, что величина  с точностью до постоянного множителя оценивается сверху величиной,
пропорциональной
с точностью до постоянного множителя оценивается сверху величиной,
пропорциональной 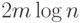 , то есть принадлежит
, то есть принадлежит 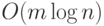 .
.
Величина  является амортизационной оценкой времени
выполнения операции СЛИТЬ, то есть величиной
является амортизационной оценкой времени
выполнения операции СЛИТЬ, то есть величиной  .
.
Замечание.
Вначале коллекция, состоящая из 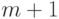 куч,
к которым применяются
куч,
к которым применяются  операций СЛИТЬ, может иметь произвольное
количество узлов, в сумме равное
операций СЛИТЬ, может иметь произвольное
количество узлов, в сумме равное  . Важно, чтобы потенциал каждой
из них, следовательно, и суммарный потенциал был равен нулю, то есть кучи не
должны первоначально иметь тяжелых узлов.
. Важно, чтобы потенциал каждой
из них, следовательно, и суммарный потенциал был равен нулю, то есть кучи не
должны первоначально иметь тяжелых узлов.
Это могут быть, например, кучи, целиком являющиеся левыми путями. Крайний
случай — это куча высоты  с минимальным количеством узлов,
не имеющая тяжелых узлов, а также это могут быть кучи с заполненным последним
уровнем узлов. Другой крайний случай — это куча высоты
с минимальным количеством узлов,
не имеющая тяжелых узлов, а также это могут быть кучи с заполненным последним
уровнем узлов. Другой крайний случай — это куча высоты  с максимальным количеством узлов, не имеющая тяжелых узлов. Остальные
варианты являются промежуточными.
с максимальным количеством узлов, не имеющая тяжелых узлов. Остальные
варианты являются промежуточными.
Особое значение имеет случай, когда каждая из 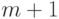 начальных
куч состоит из единственного узла.
начальных
куч состоит из единственного узла.
Итак, для всех коллекций таких куч амортизационное время выполнения одной
операции СЛИТЬ является величиной  , где
, где  — общее количество их узлов.
— общее количество их узлов.


