|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Выборочные исследования
Биномиальная модель выборки. Она применяется для описания ответов на закрытые вопросы, имеющие две подсказки, например, "да" и "нет". Конечно, пары подсказок могут быть иными. Например, "согласен" и "не согласен". Или при опросе потребителей кондитерских товаров первая подсказка может иметь такой вид: "Больше люблю "Марс", чем "Сникерс". А вторая тогда такова: "Больше люблю "Сникерс", чем "Марс".
Пусть объем выборки равен  . Тогда ответы опрашиваемых можно представить как
. Тогда ответы опрашиваемых можно представить как  , где
, где 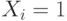 , если
, если  -й респондент выбрал первую подсказку, и
-й респондент выбрал первую подсказку, и 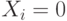 , если
, если  -й респондент выбрал вторую подсказку,
-й респондент выбрал вторую подсказку, 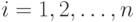 . В вероятностной модели предполагается, что случайные величины
. В вероятностной модели предполагается, что случайные величины  независимы и одинаково распределены. Поскольку эти случайные величины принимают два значения, то ситуация описывается одним параметром
независимы и одинаково распределены. Поскольку эти случайные величины принимают два значения, то ситуация описывается одним параметром  - долей выбирающих первую подсказку во всей генеральной совокупности. Тогда
- долей выбирающих первую подсказку во всей генеральной совокупности. Тогда
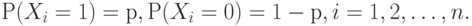
Пусть 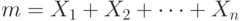 . Оценкой вероятности
. Оценкой вероятности  является частота
является частота 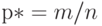 . При этом математическое ожидание
. При этом математическое ожидание  и дисперсия
и дисперсия 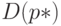 имеют вид
имеют вид

По Закону Больших Чисел (ЗБЧ) теории вероятностей (в данном случае - про теореме Бернулли) частота 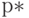 сходится (т.е. безгранично приближается) к вероятности
сходится (т.е. безгранично приближается) к вероятности  при росте объема выборки. Это и означает, что оценивание проводится тем точнее, чем больше объем выборки. Точность оценивания можно указать. Займемся этим.
при росте объема выборки. Это и означает, что оценивание проводится тем точнее, чем больше объем выборки. Точность оценивания можно указать. Займемся этим.
По теореме Муавра-Лапласа теории вероятностей
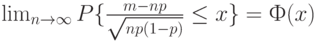
где 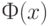 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1,
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1,

где 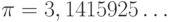 -отношение длины окружности к ее диаметру,
-отношение длины окружности к ее диаметру,  - основание натуральных логарифмов. График плотности стандартного нормального распределения
- основание натуральных логарифмов. График плотности стандартного нормального распределения

очень точно изображен на германской денежной банкноте в 10 немецких марок. Эта банкнота посвящена великому немецкому математику Карлу Гауссу (1777-1855), среди основных работ которого есть относящиеся к нормальному распределению. В настоящее время нет необходимости вычислять функцию стандартного нормального распределения и ее плотность по приведенным выше формулам, поскольку давно составлены подробные таблицы (см., например, [3]), а распространенные программные продукты содержат алгоритмы нахождения этих функций.
С помощью теоремы Муавра-Лапласа могут быть построены доверительные интервалы для неизвестной эконометрику вероятности. Сначала заметим, что из этой теоремы непосредственно следует, что
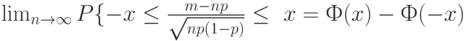
Поскольку функция стандартного нормального распределения симметрична относительно  , т.е.
, т.е.  то
то 
Зададим доверительную вероятность  . Пусть
. Пусть  удовлетворяет условию
удовлетворяет условию

т.е.
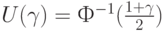
Из последнего предельного соотношения следует, что
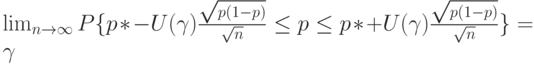
К сожалению, это соотношение нельзя непосредственно использовать для доверительного оценивания, поскольку верхняя и нижняя границы зависят от неизвестной вероятности. Однако с помощью метода наследования сходимости [4, п.2.4] можно доказать, что
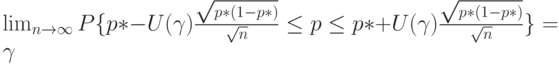
Следовательно, нижняя доверительная граница имеет вид

в то время как верхняя доверительная граница такова:

Наиболее распространенным (в прикладных исследованиях) значением доверительной вероятности является  Иногда употребляют термин "95% доверительный интервал". Тогда
Иногда употребляют термин "95% доверительный интервал". Тогда 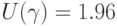
Пример. Пусть  . Тогда
. Тогда 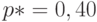 . Найдем доверительный интервал для
. Найдем доверительный интервал для 

Таким образом, хотя в достаточно большой выборке 40% респондентов говорят "да", можно утверждать лишь, что во всей генеральной совокупности таких от 35,7% до 44,3% - крайние значения отличаются на 8,6%.
Замечание. С достаточной для практики точностью можно заменить 1,96 на 2.
Удобные для использования в практической работе маркетолога и социолога таблицы точности оценивания разработаны во ВЦИОМ (Всероссийском центре по изучению общественного мнения). Приведем здесь несколько модифицированный вариант одной из них.
Объем группы Доля 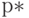
|
1000 | 750 | 600 | 400 | 200 | 100 |
|---|---|---|---|---|---|---|
| Около 10% или 90% | 2 | 3 | 3 | 4 | 5 | 7 |
| Около 20% или 80% | 3 | 4 | 4 | 5 | 7 | 9 |
| Около 30% или 70% | 4 | 4 | 4 | 6 | 9 | 10 |
| Около 40% или 60% | 4 | 4 | 5 | 6 | 8 | 11 |
| Около 50% | 4 | 4 | 5 | 6 | 8 | 11 |
В условиях рассмотренного выше примера надо взять вторую снизу строку. Объема выборки 500 нет в таблице, но есть объемы 400 и 600, которым соответствуют ошибки в 6% и 5% соответственно. Следовательно, в условиях примера целесообразно оценить ошибку как 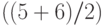 . Эта величина несколько больше, чем рассчитанная выше (4,3%). С чем связано это различие? Дело в том, что таблица ВЦИОМ связана не с доверительной вероятностью
. Эта величина несколько больше, чем рассчитанная выше (4,3%). С чем связано это различие? Дело в том, что таблица ВЦИОМ связана не с доверительной вероятностью  а с доверительной вероятностью
а с доверительной вероятностью  которой соответствует множитель
которой соответствует множитель  .Расчет ошибки по приведенным выше формулам дает 5,65%, что практически совпадает со значением, найденным по табл.2.5.
.Расчет ошибки по приведенным выше формулам дает 5,65%, что практически совпадает со значением, найденным по табл.2.5.
Минимальный из обычно используемых объемов выборки n в маркетинговых или социологических исследованиях - 100, максимальный - до 5000 (обычно в исследованиях, охватывающих ряд регионов страны, т.е. фактически разбивающихся на ряд отдельных исследований - как в ряде исследований ВЦИОМ). По данным Института социологии Российской академии наук [5], среднее число анкет в социологическом исследовании не превышает 700. Поскольку стоимость исследования растет по крайней мере как линейная функция объема выборки, а точность повышается как квадратный корень из этого объема, то верхняя граница объема выборки определяется обычно из экономических соображений. Объемы пилотных исследований (т.е. проводящихся впервые, предварительно или как первые в сериях подобных) обычно ниже, чем объемы исследований по обкатанной программе.
Нижняя граница определяется тем, что в минимальной по численности анализируемой подгруппе должно быть несколько десятков человек (не менее 30), поскольку по ответам попавших в эту подгруппу необходимо сделать обоснованные заключения о предпочтениях соответствующей подгруппы в совокупности всех потребителей растворимого кофе. Учитывая деление опрашиваемых на продавцов и покупателей, на мужчин и женщин, на четыре градации по возрасту и восемь - по роду занятий, наличие 5 - 6 подсказок во многих вопросах, приходим к выводу о том, что в рассматриваемом проекте объем выборки должен быть не менее 400 - 500. Вместе с тем существенное превышение этого объема нецелесообразно, поскольку исследование является пилотным.
Поэтому объем выборки был выбран равным 500. Анализ полученных результатов (см. ниже) позволяет утверждать, что в соответствии с целями исследования выборку следует считать репрезентативной.
