|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистика интервальных данных
Основные идеи статистики интервальных данных
Перспективная и быстро развивающаяся область статистических исследований последних лет - статистика интервальных данных. Речь идет о развитии эконометрических методов в ситуации, когда статистические данные - не числа, а интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин.
В настоящее время признается необходимым изучение устойчивости (робастности) оценок параметров к малым отклонениям исходных данных и предпосылок модели. Однако популярная среди теоретиков (см. ниже в "Проблемы устойчивости эконометрических процедур" ) модель засорения (Тьюки-Хьюбера) представляется не вполне адекватной. Эта модель нацелена на изучение влияния больших "выбросов". Поскольку любые реальные измерения лежат в некотором фиксированном диапазоне, а именно, заданном в техническом паспорте средства измерения, то зачастую выбросы не могут быть слишком большими. Поэтому представляются полезными иные, более общие схемы устойчивости, в частности, рассмотренные в "Проблемы устойчивости эконометрических процедур" ниже, в которых, например, учитываются отклонения распределений результатов наблюдений от предположений модели.
В одной из таких схем изучается влияние интервальности исходных данных на статистические выводы. Необходимость такого изучения стала для нас очевидной следующим образом. В государственных стандартах СССР по прикладной статистике в обязательном порядке давалось справочное приложение "Примеры применения правил стандарта". При разработке ГОСТ 11.011-83 (см. издание [1]) нам были переданы для анализа реальные данные о наработке резцов до предельного состояния (в часах). Оказалось, что все эти данные представляли собой либо целые числа, либо полуцелые (т.е. после умножения на 2 становящиеся целыми). Ясно, что исходная длительность наработок резцов до отказа искажена. Необходимо учесть в статистических процедурах наличие такого искажения исходных данных. Как это сделать?
Первое, что приходит в голову - модель группировки данных, согласно которой для истинного случайного значения  (мысленно) проводится замена на ближайшее число из множества
(мысленно) проводится замена на ближайшее число из множества 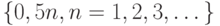 . Однако эту модель нельзя принимать без обсуждения, ее целесообразно подвергнуть сомнению, а также рассмотреть иные модели. Так, возможно, что
. Однако эту модель нельзя принимать без обсуждения, ее целесообразно подвергнуть сомнению, а также рассмотреть иные модели. Так, возможно, что  надо приводить к ближайшему сверху элементу указанного множества - если проверка качества поставленных на испытание резцов проводилась раз в полчаса. Другой вариант модели: если расстояния от
надо приводить к ближайшему сверху элементу указанного множества - если проверка качества поставленных на испытание резцов проводилась раз в полчаса. Другой вариант модели: если расстояния от  до двух ближайших элементов множества
до двух ближайших элементов множества 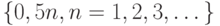 примерно равны, то естественно ввести рандомизацию при выборе заменяющего числа, и т.д.
примерно равны, то естественно ввести рандомизацию при выборе заменяющего числа, и т.д.
Наиболее адекватной представляется новая эконометрическая модель, согласно которой результаты наблюдений - не числа, а интервалы. Например, если в таблице приведено значение 53,5, то это значит, что реальное значение - какое-то число от 53,0 до 54,0, т.е. какое-то число в интервале [53,5-0,5; 53,5+0,5], где 0,5 - максимально возможная погрешность. Принимая эту модель, мы попадаем в научную область под названием "статистика интервальных данных". Она идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы (см., например, монографию [2] академика РАН Ю.И. Шокина). Это направление математики является дальнейшим развитием всем известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции. Как видно из сборника трудов Международной конференции по интервальным и стохастическим методам в науке и технике (ИНТЕРВАЛ-92), к настоящему времени удалось решить, в частности, ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов. По мнению ряда специалистов, статистика интервальных данных является частью интервальной математики [7]. Впрочем, есть другая точка зрения, согласно которой такое включение нецелесообразно, поскольку статистика интервальных данных использует несколько иные подходы к алгоритмам анализа реальных данных, чем сложившиеся в интервальной математике (подробнее см. ниже).
Общее описание направлений статистического анализа интервальных данных. Ниже развиваются асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом - уменьшаются до нуля погрешности. В частности, еще в начале 1980-х годов с помощью такой асимптотической теории были сформулированы правила выбора метода оценивания параметров гамма-распределения в ГОСТ 11.011-83 [1].
Разработана общая схема исследования, включающая расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания и дисперсии, медианы и коэффициента вариации, параметров гамма-распределения и характеристик аддитивных статистик, при проверке гипотез о параметрах нормального распределения, в т.ч. с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих - оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных, найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия. Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов. В частности, изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы. Начата разработка интервального дискриминантного анализа, в частности, рассмотрено влияние интервальности данных на показатель качества классификации.
Как показала, в частности, международная конференция ИНТЕРВАЛ-92, в области асимптотической математической статистики интервальных данных российская научная школа имеет мировой приоритет. По нашему мнению, со временем во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, "параллельные" обычно используемым алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений, сблизить позиции метрологов и статистиков.
Многие из утверждений статистики интервальных данных весьма отличаются от аналогов из классической математической статистики. В частности, не существует состоятельных оценок; средний квадрат ошибки оценки, как правило, асимптотически равен сумме дисперсии оценки, рассчитанной согласно классической теории, и некоторого положительного числа (равного квадрату т.н. нотны - максимально возможного отклонения значения статистики из-за погрешностей исходных данных) - в результате метод моментов оказывается иногда точнее метода максимального правдоподобия; нецелесообразно увеличивать объем выборки сверх некоторого предела (называемого рациональным объемом выборки) - вопреки классической теории, согласно которой чем больше объем выборки, тем точнее выводы.
История развития статистики интервальных данных противоречива. Так, в стандарт [1] был включен специальный раздел 5, посвященный выбору метода оценивания при неизвестных параметрах формы и масштаба и известном параметре сдвига, он был основан на концепциях статистики интервальных данных. Однако теоретическое обоснование этого раздела стандарта было опубликовано лишь через 5 лет. Следует отметить, что хотя в 1982 г. при разработке стандарта [1] уже были найдены основные идеи статистики интервальных данных, однако они не были полностью реализованы в нормативном документе (ГОСТ 11.011-83), и этот стандарт написан в основном в классической манере. Развитие идей статистики интервальных данных продолжается уже в течение 20 лет, и еще много чего надо сделать! Большое значение статистики интервальных данных для современной прикладной статистики обосновано в статье [3].
Одна из ведущая научная школа в области статистики интервальных данных - это школа проф. А.П. Вощинина, активно работающая с конца 70-х годов. Полученные результаты отражены в ряде монографий (см., в частности, [4], [5], [6]), статей [7], научных докладов, в том числе в трудах Международной конференции ИНТЕРВАЛ-92, диссертаций. В частности, изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности. Рассмотренное ниже направление исследований отличается нацеленностью на асимптотические результаты, полученные при больших объемах выборок и малых погрешностях измерений, поэтому оно и названо асимптотической статистикой интервальных данных.
Сформулируем сначала основные идеи асимптотической математической статистики интервальных данных, а затем рассмотрим реализацию этих идей на некоторых из перечисленных выше примеров. Следует сразу подчеркнуть, что основные идеи достаточно просты, в то время как их проработка в конкретных ситуациях зачастую оказывается достаточно трудоемкой.
Основные понятия асимптотической математической статистики интервальных данных. Пусть существо реального явления описывается выборкой 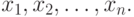 В вероятностной теории математической статистики, из которой мы исходим (см. приложение 1), выборка - это набор независимых в совокупности одинаково распределенных случайных величин. Однако беспристрастный и тщательный анализ подавляющего большинства реальных задач показывает, что статистику известна отнюдь не выборка
В вероятностной теории математической статистики, из которой мы исходим (см. приложение 1), выборка - это набор независимых в совокупности одинаково распределенных случайных величин. Однако беспристрастный и тщательный анализ подавляющего большинства реальных задач показывает, что статистику известна отнюдь не выборка 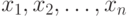 , а величины
, а величины
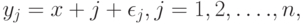
где 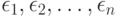 некоторые погрешности измерений, наблюдений, анализов, опытов, исследований (например, инструментальные ошибки).
некоторые погрешности измерений, наблюдений, анализов, опытов, исследований (например, инструментальные ошибки).
Одна из причин появления погрешностей - запись результатов наблюдений с конечным числом значащих цифр. Дело в том, что для случайных величин с непрерывными функциями распределения событие, состоящее в попадании хотя бы одного элемента выборки в множество рациональных чисел, согласно правилам теории вероятностей имеет вероятность 0, а такими событиями в теории вероятностей принято пренебрегать. Поэтому при рассуждениях о выборках из нормального, логарифмически нормального, экспоненциального, равномерного, гамма - распределений, распределения Вейбулла-Гнеденко и др. приходится принимать, что эти распределения имеют элементы исходной выборки 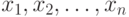 , в то время как статистической обработке доступны лишь искаженные значения
, в то время как статистической обработке доступны лишь искаженные значения 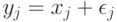 .
.
Введем обозначения
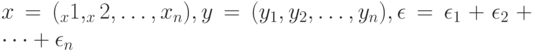
Пусть статистические выводы основываются на статистике 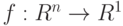 используемой для оценивания параметров и характеристик распределения, проверки гипотез и решения иных статистических задач. Принципиально важная для статистики интервальных данных идея такова: СТАТИСТИК ЗНАЕТ ТОЛЬКО
используемой для оценивания параметров и характеристик распределения, проверки гипотез и решения иных статистических задач. Принципиально важная для статистики интервальных данных идея такова: СТАТИСТИК ЗНАЕТ ТОЛЬКО 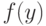 , НО НЕ
, НО НЕ 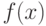 .
.
Очевидно, в статистических выводах необходимо отразить различие между 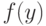 и
и 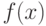 . Одним из двух основных понятий статистики интервальных данных является понятие нотны.
. Одним из двух основных понятий статистики интервальных данных является понятие нотны.
Определение. Величину максимально возможного (по абсолютной величине) отклонения, вызванного погрешностями наблюдений 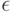 , известного статистику значения
, известного статистику значения 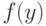 от истинного значения
от истинного значения 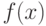 , т.е.
, т.е.

где супремум берется по множеству возможных значений вектора погрешностей 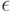 (см. ниже), будем называть НОТНОЙ.
(см. ниже), будем называть НОТНОЙ.
Если функция  имеет частные производные второго порядка, а ограничения на погрешности имеют вид
имеет частные производные второго порядка, а ограничения на погрешности имеют вид
 |
( 1) |
причем  мало, то можно показать, что нотна с точностью до бесконечно малых более высокого
мало, то можно показать, что нотна с точностью до бесконечно малых более высокого 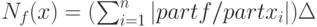 порядка имеет вид
порядка имеет вид
Условие (1) означает, что исходные данные представляются статистику в виде интервалов ![[y_i- \Delta; y_i+ \Delta], i=1,2, \dots , n](/sites/default/files/tex_cache/f293df61c8a44df419620e9e282e2ea3.png) (отсюда и название этого научного направления). Ограничения на погрешности могут задаваться разными способами - кроме абсолютных ошибок используются относительные или иные показатели различия между
(отсюда и название этого научного направления). Ограничения на погрешности могут задаваться разными способами - кроме абсолютных ошибок используются относительные или иные показатели различия между  и
и  .
.
Основные результаты в вероятностной модели. В классической вероятностной модели имеют элементы исходной выборки 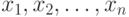 рассматриваются как независимые одинаково распределенные случайные величины. Как правило, существует некоторая константа
рассматриваются как независимые одинаково распределенные случайные величины. Как правило, существует некоторая константа 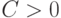 такая, что в смысле сходимости по вероятности
такая, что в смысле сходимости по вероятности
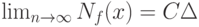 |
( 2) |
Соотношение (2) доказывается отдельно для каждой конкретной задачи.
При использовании классических эконометрических методов в большинстве случаев используемая статистика  является асимптотически нормальной. Это означает, что существуют константы
является асимптотически нормальной. Это означает, что существуют константы  и
и 

где 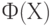 функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При этом обычно оказывается, что
функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При этом обычно оказывается, что
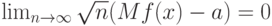
и
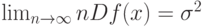
а потому в классической эконометрике средний квадрат ошибки статистической оценки равен
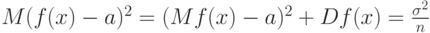
с точностью до членов более высокого порядка.
В статистике интервальных данных ситуация совсем иная - обычно можно доказать, что средний квадрат ошибки равен
 |
( 3) |
Из соотношения (3) можно сделать ряд важных следствий. Прежде всего отметим, что правая часть этого равенства, в отличие от правой части соответствующего классического равенства, не стремится к 0 при безграничном возрастании объема выборки. Она остается больше некоторого положительного числа, а именно, квадрат нотны. Следовательно, статистика  не является состоятельной оценкой параметра
не является состоятельной оценкой параметра  . Более того, состоятельных оценок вообще не существует.
. Более того, состоятельных оценок вообще не существует.
Пусть доверительным интервалом для параметра  , соответствующим заданной доверительной вероятности
, соответствующим заданной доверительной вероятности  , в классической математической статистике является интервал
, в классической математической статистике является интервал 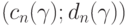 В статистике интервальных данных аналогичный доверительный интервал является более широким. Он имеет вид
В статистике интервальных данных аналогичный доверительный интервал является более широким. Он имеет вид  Таким образом, его длина увеличивается на две нотны. Следовательно, при увеличении объема выборки длина доверительного интервала не может стать меньше, чем
Таким образом, его длина увеличивается на две нотны. Следовательно, при увеличении объема выборки длина доверительного интервала не может стать меньше, чем 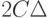 (см. формулу (2)).
(см. формулу (2)).
В статистике интервальных данных методы оценивания параметров имеют другие свойства по сравнению с классической математической статистикой. Так, при больших объемах выборок метод моментов может быть заметно лучше, чем метод максимального правдоподобия (т.е. иметь меньший средний квадрат ошибки - см. формулу (3)), в то время как в классической математической статистике второй из названных методов всегда не хуже первого.
Рациональный объем выборки. Анализ формулы (3) показывает, что в отличие от классической математической статистики нецелесообразно безгранично увеличивать объем выборки, поскольку средний квадрат ошибки остается всегда большим квадрата нотны. Поэтому представляется полезным ввести понятие "рационального объема выборки" 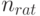 при достижении которого продолжать наблюдения нецелесообразно.
при достижении которого продолжать наблюдения нецелесообразно.
Как установить "рациональный объем выборки"? Можно воспользоваться идеей "принципа уравнивания погрешностей", выдвинутой в монографии [8]. Речь идет о том, что вклад погрешностей различной природы в общую погрешность должен быть примерно одинаков. Этот принцип дает возможность выбирать необходимую точность оценивания тех или иных характеристик в тех случаях, когда это зависит от исследователя. В статистике интервальных данных в соответствии с "принципом уравнивания погрешностей" предлагается определять рациональный объем выборки 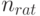 из условия равенства двух величин - метрологической составляющей, связанной с нотной, и статистической составляющей - в среднем квадрате ошибки (3), т.е. из условия
из условия равенства двух величин - метрологической составляющей, связанной с нотной, и статистической составляющей - в среднем квадрате ошибки (3), т.е. из условия
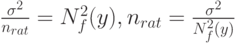
Для практического использования выражения для рационального объема выборки неизвестные теоретические характеристики необходимо заменить их оценками. Это делается в каждой конкретной задаче по-своему.
Исследовательскую программу в области статистики интервальных данных можно "в двух словах" сформулировать так: для любого эконометрического алгоритма анализа данных (алгоритма прикладной статистики) необходимо вычислить нотну и рациональный объем выборки (или иные величины из того же понятийного ряда, возникающие в многомерном случае, при наличии нескольких выборок и при иных обобщениях описываемой здесь простейшей схемы). Затем проследить влияние погрешностей исходных данных на точность оценивания, доверительные интервалы, значения статистик критериев при проверке гипотез, уровни значимости и другие характеристики статистических выводов. Очевидно, классическая математическая статистика является частью статистики интервальных данных, выделяемой условием 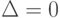 .
.
