Цвет в компьютерной графике
Пространство CIE Luv
Один из существенных минусов цветового пространства XYZ — это то, что оно не является перцептивно (визуально) равномерным и не может использоваться для вычисления цветовых расстояний. Поэтому CIE (МКО) продолжила разработку перцептивно равномерного пространства. Целью комитета CIE было создание повторяемой системы стандартов цветопередачи для производителей красок, чернил, пигментов и других красителей. Самая важная функция этих стандартов — предоставить универсальную схему, в рамках которой можно было бы устанавливать соответствие цветов.
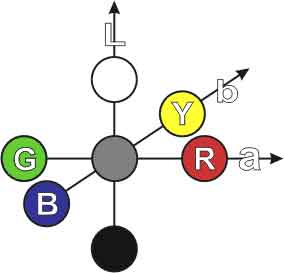
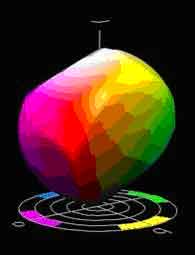
В результате было создано цветовое пространство CIE Luv, позволяющее определить различение цветов для человека с "усредненным" зрением, (т.е. различные люди неодинаково воспринимают разницу между цветами). Свое название пространство получило благодаря его компонентам L, u и v. Параметр L соответствует яркости цвета, u отвечает за переход от зеленого к красному (при увеличении), а при увеличении параметра v происходит переход от синего к фиолетовому. Если u и v равны 0, то, меняя L, получаем цвета, являющиеся градациями серого.
Это цветовое пространство было разработано для количественного измерения различия двух цветов. CIE были проведены исследования с участием большого числа людей, результатом чего явилось создание пространства Luv. Измерения проводились в "хороших" условиях (достаточное освещение и неяркий монотонный фон); перед испытуемым находились два листа бумаги, окрашенных соответственно двумя цветами, и он должен был дать ответ, насколько, по его мнению, различаются эти цвета. В случае реальных изображений мы должны находить различия между цветами на более сложном фоне, при этом не всегда при хорошем освещении (например, слишком ярком). Но освещение зависит и от помещения, и от времени суток, и от того, под каким углом находится поверхность к источнику света.
Переход из RGB в Luv осуществляется следующим образом. Сначала нормируем R, G, B:
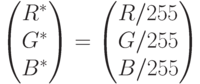
Далее совершаем преобразование пространства RGB в XYZ:
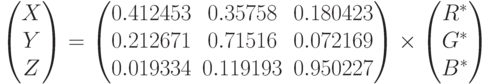
Цветовое пространство CIE Luv — непрерывное однородное преобразование пространства CIE XYZ, описываемое следующими формулами:
![\begin{aligned}
& L=
\left\{
\begin{aligned}
& 116 \times \sqrt[3]{\frac{Y}{Y_n}}-16, \quad \frac{Y}{Y_n}>0.008856 \\
& 903.3 \times \frac{Y}{Y_n}, \quad \frac{Y}{Y_n} \le 0.008856
\end{aligned}
\right. \\
& u'=\frac{4X}{X+15Y+3Z}=\frac{4x}{-2x+12y+3}, \quad v'=\frac{9Y}{X+15Y+3Z}=\frac{9y}{-2x+12y+3} \\
& u=13L(u'-u_n), \quad v=13L(v'-v_n)
\end{aligned}](/sites/default/files/tex_cache/bac8146d9df8133b886065dcf9b5738a.png)
Для определения параметров 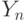 ,
, 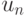 и
и 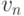 , вводится понятие белой точки
( white point ). Белая точка - это пара параметров цветности (x, y),
определяющая эталон белого цвета для различных источников света. CIE
составила таблицу белых точек для источников света разной яркости. При
этом значение компоненты Y белой точки в XYZ нормализовано до 100 (в
приведенных выше формулах
, вводится понятие белой точки
( white point ). Белая точка - это пара параметров цветности (x, y),
определяющая эталон белого цвета для различных источников света. CIE
составила таблицу белых точек для источников света разной яркости. При
этом значение компоненты Y белой точки в XYZ нормализовано до 100 (в
приведенных выше формулах 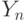 как раз соответствует нормализованной Y
компоненте). Параметры
как раз соответствует нормализованной Y
компоненте). Параметры 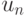 и
и 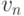 вычисляются по тем же формулам, что
вычисляются по тем же формулам, что 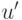 и
и 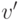 ,
в которых используются значения x и y для белой точки.
,
в которых используются значения x и y для белой точки.
Как уже упоминалось выше, компонента L соответствует яркости цвета, а из формул видно, что L пропорциональна кубическому корню из компоненты Y пространства XYZ. Однако существует мнение, что человеческому восприятию больше соответствует корень второй степени из освещенности. Так, например, в цветовом пространстве Lab параметр L вычисляется с использованием кубического корня.
Немного о свойствах величин L, u, v:
- L меняется от 0 до 100;
- u, v лежат в пределах -200, 200;
- u отвечает за переход от зеленого к красному (при увеличении u);
- v отвечает за переход от синего к фиолетовому (при увеличении v);
- если u и v равны 0, меняя L, получаем изображение, содержащее градации серого (grayscale).
Наконец, самое важное, к чему мы стремились, переходя в это
пространство. Нам заданы два цвета -  и
и  . Как определить расстояние
между цветами, то есть насколько человек заметил бы различие между
ними? Оказывается, оно задается евклидовой нормой
. Как определить расстояние
между цветами, то есть насколько человек заметил бы различие между
ними? Оказывается, оно задается евклидовой нормой
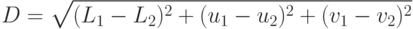
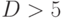 большинство людей уже замечают
различие, при
большинство людей уже замечают
различие, при 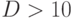 оно заметно всем. В этом и состоит главное достоинство
этого пространства. Оно учитывает восприятие цветов человеком, и
различие между цветами определяется очень простой формулой. Необходимо
заметить, что эта формула применима в определенных условиях:
освещение, фон не должны мешать и отвлекать.
оно заметно всем. В этом и состоит главное достоинство
этого пространства. Оно учитывает восприятие цветов человеком, и
различие между цветами определяется очень простой формулой. Необходимо
заметить, что эта формула применима в определенных условиях:
освещение, фон не должны мешать и отвлекать.Одновременно с разработкой CIE Luv было также разработано перцептивно равномерное цветовое пространство CIE Lab. Из этих двух моделей более широко применяется модель CIE Lab. Структура цветового пространства Lab основана на той теории, что цвет не может быть одновременно зеленым и красным или желтым и синим (рис. 2.14). Следовательно, для описания атрибутов "красный/зеленый" и "желтый/синий" можно воспользоваться одними и теми же значениями. Формулы перехода от пространства XYZ к пространству Lab осуществляется следующим образом:
![\begin{aligned}
& L=
\left\{
\begin{aligned}
& 116 \cdot [(Y/Y_n)^{1/3}]-16 & \text{если } (Y/Y_n)>0.008856 &\quad a=500\cdot [f(X/X_n)-f(Y/Y_n)] \\
& 903.3 \cdot Y/Y_n & \text{если } (Y/Y_n) \le 0.008856 &\quad b=200\cdot [f(Y/Y_n)-f(Z/Z_n)]
\end{aligned}
\right. \\
& \text{где } f(t)=
\left\{
\begin{aligned}
& t^{1/3} & \text{если } (Y/Y_n)>0.008856 \\
& 7.787 \cdot t + 16/116 & \text{если } (Y/Y_n)\le 0.008856
\end{aligned}
\right.
\end{aligned}](/sites/default/files/tex_cache/1f2818810bf8da1d172271b586b57d2a.png)
Каждая цветовая модель, помимо преимуществ, также имеет и свои индивидуальные недостатки. Существуют и другие модели, которые здесь не рассматриваются.
Вопросы и упражнения
- Расположите в убывающем порядке чувствительность рецепторов глаза к цветам: красный, зеленый, синий.
- Что такое хроматический спектр?
- Что такое ахроматический спектр?
- Как осуществляется проекция трехмерного цветового пространства на плоскость?
- Чем отличается цветовой график МКО от треугольной проекционной области цветового пространства?
- Что такое дополнительный цвет?
- Что такое аддитивная и субстрактивная цветовые модели? Чем отличаются их цветовые кубы?
- Что является основой цветовой модели HSV и HLS?
- Являются ли цветовые модели HSV и HLS аддитивными или субстрактивными?
- Постройте алгоритм преобразования модели RGB в HSV.
- Постройте алгоритм преобразования модели RGB в HLS.
- В чем состоит главное достоинство цветового пространства Luv?
- В чем состоит главное достоинство цветового пространства Lab?