Удаление невидимых поверхностей и линий
Задача удаления невидимых линий и поверхностей является одной из наиболее интересных и сложных в компьютерной графике. Алгоритмы удаления заключаются в определении линий ребер, поверхностей или объемов, которые видимы или невидимы для наблюдателя, находящегося в заданной точке пространства.
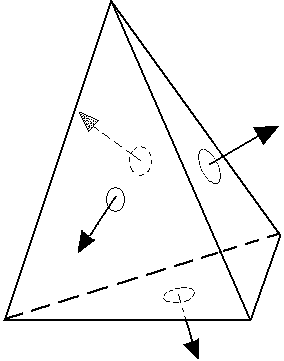
Необходимость удаления невидимых линий, ребер, поверхностей или объемов проиллюстрирована на рис. 6.1. Рисунок наглядно демонстрирует, что изображение без удаления невидимых линий воспринимается неоднозначно.
Сложность задачи удаления невидимых линий и поверхностей привела к появлению большого числа различных способов ее решения. Многие из них ориентированы на специализированные приложения. Единого (общего) решения этой задачи, годного для различных случаев, естественно, не существует: для каждого случая выбирается наиболее подходящий метод. Например, для моделирования процессов в реальном времени требуются быстрые алгоритмы, в то время как для формирования сложного реалистического изображения, в котором представлены тени, прозрачность и фактура, учитывающие эффекты отражения и преломления цвета в мельчайших оттенках, фактор времени выполнения уже не так существенен. Подобные алгоритмы работают медленно, и зачастую на вычисления требуется несколько минут или даже часов. Существует тесная взаимосвязь между скоростью работы алгоритма и детальностью его результата. Ни один из алгоритмов не может достигнуть хороших оценок для этих двух показателей одновременно. По мере создания все более быстрых алгоритмов можно строить все более детальные изображения. Реальные задачи, однако, всегда будут требовать учета еще большего количества деталей.
Все алгоритмы такого рода так или иначе включают в себя сортировку, причем главная сортировка ведется по геометрическому расстоянию от тела, поверхности, ребра или точки до точки наблюдения или картинной плоскости. Основная идея, положенная в основу сортировки по расстоянию, заключается в том, что чем дальше расположен объект от точки наблюдения, тем больше вероятность, что он будет полностью или частично заслонен одним из объектов, более близких к точке наблюдения. После определения расстояний или приоритетов по глубине остается провести сортировку по горизонтали и по вертикали, чтобы выяснить, будет ли рассматриваемый объект действительно заслонен объектом, расположенным ближе к точке наблюдения. Эффективность любого алгоритма удаления в значительной мере зависит от эффективности процесса сортировки.
Алгоритмы удаления невидимых линий или поверхностей можно классифицировать по способу выбора системы координат или пространства, в котором они работают. Алгоритмы, работающие в объектном пространстве, имеют дело с мировой системой координат, в которой описаны эти объекты. При этом получаются весьма точные результаты, ограниченные, вообще говоря, лишь погрешностью вычислений. Полученные изображения можно свободно масштабировать. Алгоритмы, работающие в объектном пространстве, особенно полезны в тех приложениях, где необходима высокая точность. Алгоритмы же, работающие в пространстве изображения, имеют дело с системой координат того экрана, на котором объекты визуализируются. При этом точность вычислений ограничена разрешающей способностью экрана.
Мы приведем некоторые из алгоритмов, работающих как в объектном пространстве, так и в пространстве изображения, каждый из которых иллюстрирует одну или несколько основополагающих идей теории алгоритмов удаления невидимых линий и поверхностей.
Удаление нелицевых граней многогранника
Алгоритм Робертса
Этот алгоритм, предложенный в 1963 г., является первой разработкой такого рода и предназначен для удаления невидимых линий при штриховом изображении объектов, составленных из выпуклых многогранников. Он относится к алгоритмам, работающим в объектном пространстве, и очень элегантен с математической точки зрения. В нем очень удачно сочетаются геометрические методы и методы линейного программирования.
Выпуклый многогранник однозначно определяется набором плоскостей,
образующих его грани, поэтому исходными данными для алгоритма являются
многогранники, заданные списком своих граней. Грани задаются в виде
плоскостей, заданных в канонической форме (см.
"Геометрические преобразования"
) в объектной
системе координат: 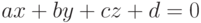 .
.
Таким образом, каждая плоскость определяется четырехмерным вектором 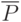 , а каждая точка
, а каждая точка 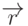 , заданная в однородных координатах, также
представляет собой четырехмерный вектор:
, заданная в однородных координатах, также
представляет собой четырехмерный вектор:
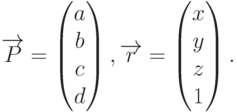
Принадлежность точки плоскости можно установить с помощью
скалярного произведения, т.е. если 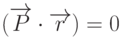 , то точка принадлежит плоскости,
если же нет, то знак произведения показывает, по какую сторону от
плоскости эта точка находится. В алгоритме Робертса плоскости строятся
таким образом, что внутренние точки многогранника лежат в
положительной полуплоскости. Это означает, что вектор
, то точка принадлежит плоскости,
если же нет, то знак произведения показывает, по какую сторону от
плоскости эта точка находится. В алгоритме Робертса плоскости строятся
таким образом, что внутренние точки многогранника лежат в
положительной полуплоскости. Это означает, что вектор 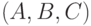 является внешней нормалью к многограннику (рис. 6.2). Из векторов плоскостей
строится прямоугольная матрица порядка
является внешней нормалью к многограннику (рис. 6.2). Из векторов плоскостей
строится прямоугольная матрица порядка 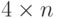 , которая называется обобщенной матрицей описания многогранника:
, которая называется обобщенной матрицей описания многогранника:
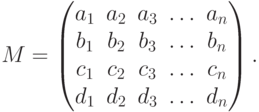
Умножая столбцы матрицы на вектор 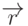 , получим n -мерный вектор, и
если все его компоненты неотрицательны, то точка принадлежит
многограннику. Это условие будем записывать в виде
, получим n -мерный вектор, и
если все его компоненты неотрицательны, то точка принадлежит
многограннику. Это условие будем записывать в виде 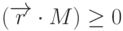 (имеется в виду
умножение вектор-строки на матрицу).
(имеется в виду
умножение вектор-строки на матрицу).
В своем алгоритме Робертс рассматривает только отрезки, являющиеся пересечением граней многогранника.
Из обобщенной матрицы можно получить информацию о том, какие грани
многогранника пересекаются в вершинах. Действительно, если вершина 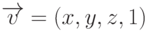 принадлежит граням
принадлежит граням 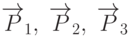 , то она удовлетворяет уравнениям
, то она удовлетворяет уравнениям
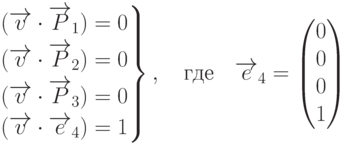
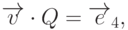
 - матрица, составленная из вектор-столбцов
- матрица, составленная из вектор-столбцов 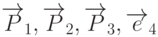 . Значит, координаты
вершины определяются соотношением
. Значит, координаты
вершины определяются соотношением
Алгоритм прежде всего удаляет из каждого многогранника те ребра или грани, которые экранируются самим телом. Робертс использовал для этого простой тест: если одна или обе смежные грани обращены своей внешней поверхностью к наблюдателю, то ребро является видимым. Тест этот выполняется вычислением скалярного произведения координат наблюдателя на вектор внешней нормали грани: если результат отрицательный, то грань видима.
Затем каждое из видимых ребер каждого многогранника сравнивается с каждым из оставшихся многогранников для определения того, какая его часть или части, если таковые есть, экранируются этими телами. Для этого в каждую точку ребра проводится отрезок луча, выходящего из точки расположения наблюдателя. Если отрезок не пересекает ни одного из многогранников, то точка видима. Для решения этой задачи используются параметрические уравнения прямой, содержащей ребро, и луча.
Если заданы концы отрезка 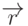 и
и 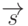 , а наблюдатель расположен в точке
, а наблюдатель расположен в точке 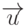 , то отрезок задается уравнением
, то отрезок задается уравнением

 , - уравнением
, - уравнением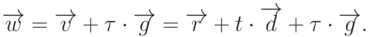
Для определения той части отрезка, которая закрывается каким-либо
телом, достаточно найти значения  и
и  , при которых произведение
вектора
, при которых произведение
вектора 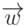 на обобщенную матрицу положительно. Для каждой плоскости
на обобщенную матрицу положительно. Для каждой плоскости  записывается неравенство
записывается неравенство
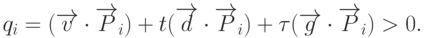
Полагая 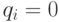 , получаем систему уравнений, решения которой дают нам
точки "смены видимости" отрезка. Результат можно получить путем
совместного решения всевозможных пар уравнений из этой системы. Число
всевозможных решений при
, получаем систему уравнений, решения которой дают нам
точки "смены видимости" отрезка. Результат можно получить путем
совместного решения всевозможных пар уравнений из этой системы. Число
всевозможных решений при  плоскостях равно
плоскостях равно 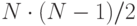 .
.
Так как объем вычислений растет с увеличением числа многоугольников, то желательно по мере возможности сокращать их число, т.е. если мы аппроксимируем некоторую поверхность многогранником, то в качестве граней можно использовать не треугольники, а более сложные многоугольники. При этом, разумеется, встает проблема, как построить такой многоугольник, чтобы он мало отклонялся от плоской фигуры.