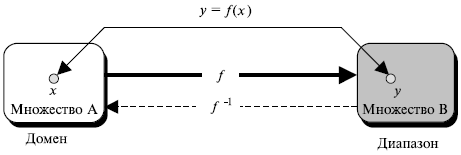НОУ ИНТУИТ | Математика криптографии и теория шифрования. Лекция 14: Криптографическая система RSA

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Уровень: специалист | Доступ: свободно

Вам нравится? Нравится 71 студенту

| Поделиться |

Поддержать программу

"Лазейка" в односторонней функции

Главная идея асимметрично-ключевой криптографии — понятие "лазейки" в односторонней функции.

Функции

Хотя понятие функции знакомо из математики, мы дадим неофициальное определение здесь. Функция — правило, по которому связывают (отображают) один элемент во множестве A, называемый доменом, и один элемент во множестве B, называемый диапазоном, как показано на рис. 14.3.

Рис. 14.3. Функция отображения домена в диапазон

Обратимая функция — функция, которая связывает каждый элемент в диапазоне с точно одним элементом в домене.

Односторонняя функция (OWF — One Way Function) — функция, которая обладает следующими двумя свойствами:

f вычисляется просто. Другими словами, при данном x может быть легко вычислен y = f (x).
f ^-1 вычисляется трудно. Другими словами, при данном y, вычислить x= f^~1 (y) неосуществимо.

"Лазейка" в односторонней функции

"Лазейка" в односторонней функции (TOWF — Trapdoor One Way) — односторонняя функция с третьим свойством:

3. При данном y и ловушке (секретной) x может быть легко вычислен.

Пример 14.1

Когда n является большим, 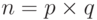$n = p \times q$ — односторонняя функция. Обратите внимание, что в этой функции x — кортеж (p, q) двух простых чисел, а y в данном случае — это n. При заданных p и q всегда просто вычислить n. При данном n очень трудно вычислить p и q. Это — проблема разложения на множители, которую мы рассматривали в лекциях 12-13. В этом случае для нахождения функции f^-1 нет решения с полиномиальным временем.

Пример 14.2

Когда n является большим, функция y = x^k mod n — "лазейка" в односторонней функции. При заданных x, k и n просто вычислить y, используя алгоритм быстрого возведения в степень, который мы обсуждали в лекциях 12-13. При заданных y, k и n очень трудно вычислить x. Это — проблема дискретного логарифма, которую мы обсуждали в лекциях 12-13. В этом случае нет решения с полиномиальным временем для функции f^-1. Однако если мы знаем "лазейку" и k’, такое, что 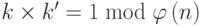$k \times k' = 1\bmod \varphi \left( n \right)$ , мы можем использовать x = y^k mod n, чтобы найти x. Это — известный алгоритм (RSA — Riverst-Shamir-Adelman), который будет рассмотрен позже в этой лекции.

Ранцевая криптосистема

Первая блестящая идея относительно криптографии открытого ключа доступа принадлежит Меркелю и Хеллману — она изложена в их ранцевой криптосистеме. Хотя эта система ненадежна в соответствии с сегодняшними стандартами, главная ее идея дает возможность понять современные криптосистемы с открытым ключом, которые будут рассматриваться позже в этой лекции.

Если нам говорят, какие элементы заранее определенного множества чисел мы имеем, то можно легко вычислить сумму чисел. Если нам говорят сумму, то трудно сказать, какие элементы "находятся в ранце".

Определение

Предположим, что нам даны два k -кортежа, a = [a₁,a₂, …,a_k] и x = [x₁,x₂, …,x_k]. Первый кортеж — заранее определенное множество; второй кортеж, в котором x равен только 0 или l, определяет, какие элементы a должны быть отброшены в ранце. Сумма элементов в ранце равна

s = knapsackSum (a, x) = x₁ a₁ + x₂ a₂ + • • • + x_ka_k

По данным a и x просто вычислить s. Однако по данному s трудно найти x. Другими словами, s = knapsackSum (x, a) вычисляется просто, но x= inv_knapmi (s, a) труден. Функция knapsackSum — односторонняя функция, если a - общий k -кортеж.

Суперувеличение кортежа

Просто вычислить knapsackSum и inv_knapsackSum, если - k -кортеж суперувеличивается. В суперувеличивающемся кортеже $a \geqslant {a_1} + {a_2} + \bullet \bullet \bullet + {a_i}_{ - 1}$ . Другими словами, каждый элемент (кроме a₁ ) больше или равен сумме всех предыдущих элементов. В этом случае мы вычисляем knapsackSum и inv_knapsackSum, как показано в Алгоритме 14.1. Алгоритм inv_knapsackSum запускается от наибольшего элемента и продолжает процесс к наименьшему. В каждой итерации он проверяет, находится ли элемент в рюкзаке.

knapsackSum (x[1,…,k], a[1,…,k] )
{
s <- 0
for (i=1 to k)
{
s <- s + a_i x x_i
}
return x
}

Inv_knapsackSum (s, a[1,…,k])
{
       for (i=k down to 1)
      {
          if s >= a_j
         {
                 x_i <- 1
                 s <- s - a_i
           }
           else x_i <- 0
       }
        return x[1,…,k]
}

14.1. knapsacksum и inv_knapsackSum для суперувеличивающегося k-кортежа

Пример 14.3

Как очень тривиальный пример, предположим, что даны a = [17, 25, 46, 94, 201, 400] и s = 272. Таблица 14.1 показывает, как найти кортеж, используя процедуру inv_knapsackSum в алгоритме 14.1.

В этом случае x = [0, 1, 1,0, 1,0], — это означает, что в рюкзаке находятся 25, 46 и 201.

Таблица 14.1. Значения i, a и x в примере 14.3
i	a_i	s	s $\ge$	x_i	s $\gets$ s - a_i x x_i
6	400	272	false	x₆=0	272
5	201	272	true	x₅=1	71
4	94	71	false	x₄=0	71
3	46	71	true	x₃=1	25
2	25	25	true	x₂=1	0
1	17	0	false	x₁=0	0

Секретная связь с использованием ранца

Посмотрим, как Алиса может передать секретное сообщение Бобу, использующему ранцевую криптосистему. Идея показана на рис. 14.4.

Рис. 14.4. Секретная связь с использованием ранцевой криптосистемы

Генерация ключей

Этот процесс:

Создает суперувеличивающийся k -кортеж b = [b₁, b₂,..., b_k].
Выбирает модуль n, такой, что n > b₁ + b₂ + • • • + b_k.
Выбирает случайное целое число r, которое является взаимно простым с n и ${\text{1}} \leqslant r \leqslant n-{\text{1}}$ .
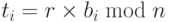Создает временный k -кортеж t = [t₁, t₂,…….. t_k], в котором ${t_i} = r \times {b_i}\bmod n$ .
Выбирает перестановку k -объектов и находит новый кортеж a = liermute(t).
Открытый ключ k -кортежа — a. Секретный ключ — n, r и k -кортеж b.

Шифрация

Предположим, что Алисе надо послать сообщение Бобу.

Алиса преобразует свое сообщение в k -кортеж x=[x₁, x₂,…. x_k], в котором x_i — не 0 и не 1. Кортеж представляет собой исходный текст.
Алиса использует knapsackSum для вычисления s в качестве исходного текста.

Дешифрация

Боб получает зашифрованный текст s.

Боб вычисляет $s' = {r^{ - 1}} \times s\bmod n$ .

Боб переставляет x’ для того, чтобы найти x. Кортеж x есть восстановленный исходный текст.

Пример 14.4

Это тривиальный (очень легко раскрываемый пример). Он приводится только для того, чтобы показать процедуру.

Генерация ключей:
- Боб создает суперувеличивающийся кортеж b = [7, 11, 19, 39, 79, 157, 313].
- Боб выбирает модуль n = 900 и r = 37, и [4 2 5 3 1 7 6] как таблицу перестановок.
- Боб теперь вычисляет кортеж t = [259, 407, 703, 543, 223, 409, 781].
- Боб теперь вычисляет кортеж a = перестановка (t)= [543, 407, 223, 703, 259, 781, 409].
- Боб объявляет a ; он сохраняет в тайне n, r и b.
Предположим, что Алиса хочет передать единственный символ "g" Бобу.
- Она использует представление ASCII на 7 битов "g", (1100111) ₂ и создает кортеж x = [1,1,0,0, 1, 1, 1]. Это — исходный текст.
- Алиса вычисляет s = knulisackSum (a, x) = 2399. Это — зашифрованный текст, передаваемый Бобу.
Боб может расшифровать зашифрованный текст, s = 2165.
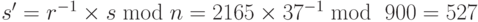- a. Боб вычисляет $s' = {r^{ - 1}} \times s\bmod n = 2165 \times {37^{ - 1}}\bmod {\text{ }}900 = 527$ .
- Боб вычисляет x’ = inv_knalisackSum (s', b) = [1, 1, 0, 1, 0, 1, 1].
- Боб вычисляет x = перестановка (x’) = [1, 1, 0, 0, 1, 1, 1]. Он интерпретирует строку (1100111) ₂ как символ "g".

Лазейка

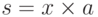Вычисление суммы элементов в ранце Алисы — фактически умножение матрицы-строки x на матрицу-столбец a. Результат — матрица s $1 \times 1$ . Матричное умножение: $s = x \times a$ , в котором x является матрицей-строкой, а a — матрица-столбец -односторонняя функция. По данным s и x Ева не сможет легко найти a. Боб, однако, имеет лазейку. Боб использует его $s' = {r^{ - 1}} \times s$ и секретную, суперувеличивающуюся матрицу-столбец b, чтобы найти матрицу-строку x. При этом он применяет процедуру inv_knapsackSum. Перестановка позволяет Бобу найти x по известному x’.