НОУ ИНТУИТ | Математика криптографии и теория шифрования. Лекция 7: Введение в основы современных шифров с симметричным ключом

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Уровень: специалист | Доступ: свободно

Вам нравится? Нравится 71 студенту

| Поделиться |

Поддержать программу

Атаки на блочные шифры

Атаки традиционных шифров могут также использоваться для современных блочных шифров, но сегодняшние блочные шифры успешно противостоят большинству атак, обсужденных в лекциях 5-6. Например, грубая силовая атака ключа, как правило, неосуществима, потому что ключи обычно имеют очень большую длину. Однако недавно были изобретены некоторые новые виды атак блочных шифров, которые основаны на структуре современных блочных шифров. Эти атаки используют методы и дифференциального, и линейного анализа.

Дифференциальный криптоанализ

Идею относительно дифференциального криптоанализа предложили Эли Бихам и Ади Шамир. Это — атака с выборкой исходного текста. Ева может каким-либо образом получить доступ к компьютеру Алисы и завладеть выборочно частью исходного текста и соответствующего зашифрованного текста. Цель состоит в том, чтобы найти ключ шифра Алисы.

Алгоритм анализа. Перед тем как Ева предпримет атаку с выборкой исходного текста, она должна проанализировать алгоритм шифрования, чтобы собрать некоторую информацию об отношениях зашифрованного и исходного текстов. Очевидно, Ева не знает ключ шифра. Однако некоторые шифры имеют слабости в структурах, которые могут позволить Еве найти различия исходного текста и различия зашифрованного текста, не зная ключ.

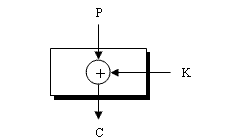
Предположим, что шифр состоит только из одной операции ИСКЛЮЧАЮЩЕЕ ИЛИ, как показано на рис. 7.18. Не зная значения ключа, Ева может легко найти отношения между разностями исходного текста и разностями зашифрованного текста. Если разность исходного текста мы обозначим $P_{1}\oplus P_{2}$ и разность зашифрованного текста мы обозначим $C_{1}\oplus C_{2}$ , приведенные следующие преобразования доказывают, что $C_{1}\oplus C_{2} = P_{1}\oplus P_{2}$ :

$C_{1} = P_{1} \oplus K C_{2} = P_{2} \oplus K \to C_{1} \oplus C_{2} = P_{1} \oplus K \oplus P_{2} \oplus K = P_{1} \oplus P_{2}$

Однако этот пример нереалистичен; модемные блочные шифры не настолько просты.

Рис. 7.18. Диаграмма для примера 7.13

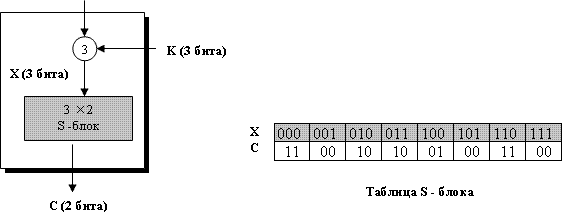
В примере 7.13 мы добавляем один S -блок, как показано на рис. 7.19.

Рис. 7.19. Диаграмма для примера 7.14

Хотя эффект шифрования ключом не действует, когда мы используем разности между двумя X и двумя P 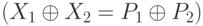$(X_{1}\oplus X_{2} = P_{1}\oplus P_{2})$ , существование S -блока мешает Еве найти и определенные отношения между разностями исходного текста и разностями зашифрованного текста. Однако возможно установить вероятностные отношения. Ева может составить таблицу 7.4, которая показывает для разности исходного текста, сколько можно создать разностей зашифрованного текста — шифр. Обращаем внимание, что таблица сделана по информации, которая произведенеа с учетом таблицы входа-выхода S -блока по рис. 7.19, потому что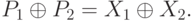 $P_{1}\oplus P_{2} = X_{1}\oplus X_{2}.$

Таблица 7.4. Дифференциальная таблица для входов и выходов для шифра в примере 7.14
	C₁ $\oplus$ C₂
P₁ $\oplus$ P₂		00	01	10	11
	000	8
	001	2	2		4
	010	2	2	4
	011		4	2	2
	100	2	2	4
	101		4	2	2
	110	4		2	2
	111			2	6

Поскольку размер ключей — 3 бита, может быть восемь случаев для каждой разности во вводе. Таблица показывает, что если входная разность — (000) ₂, разность выхода — всегда (00) ₂. С другой стороны, таблица показывает, что если входная разность — (100) ₂, то имеется два случая разностей выхода (00)₂, два случая разностей выхода (01)₂ и четыре случая разностей выхода (01)₂.

Пример 7.15

Эвристический результат примера 7.14 может создать вероятностную информацию для Евы, как показано в таблице 7.5. Входы в таблице соответствуют вероятностям появления. Разности с нулевой вероятностью никогда не будут возникать.

Таблица 7.5. Дифференциальная таблица для входов и выходов для шифра в примере 7.15
	00	01	10	11
000	1	0	0	0
001	0,25	0,25	0	0,50
010	0,25	0,25	0,50	0
011	0	0,50	0,25	0,25
100	0,25	0,25	0,50	0
101	0	0,50	0,25	0,25
110	0,50	0	0,25	0,25
111	0	0	0,25	0,75

Как мы увидим позже, Ева теперь располагает достаточным количеством информации, чтобы начать ее атаку. Таблица показывает, что вероятности распределены неоднородно из-за слабости в структуре S -блока. Таблица 7.5 упоминается иногда как дифференциальная таблица распределения или профайл ИСКЛЮЧАЮЩЕЕ ИЛИ.

Запуск атаки выборки исходного текста. После того как анализ однажды сделан, он может быть сохранен для будущего использования, пока структура шифра не изменится. Ева может выбрать для атак исходные тексты. Дифференциальная таблица распределения вероятности (таблица 7.5) поможет Еве их выбирать — она возьмет те, которые имеют самую высокую вероятность в таблице.

Предположительное значение ключа. После запуска некоторых атак с соответствующей выборкой исходного текста Ева может найти некоторую пару "исходный текст / зашифрованный текст", которая позволяет ей предположить некоторое значение ключа. Процесс начинается от C и продвигается к P.

Пример 7.16

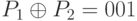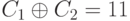Рассматривая таблицу 7.5, Ева знает, что если $P_{1}\oplus P_{2}= 001$ , то $C_{1}\oplus C_{2}= 11$ с вероятностью 0,50 ( 50 процентов). Она пробует взять C₁ = 00 и получает P₁ = 010 (атака с выборкой зашифрованного текста). Она еще пробует C₂ = 11 и получает P₂ = 011 (другая атака с выборкой зашифрованного текста). Теперь она пробует вернуться к анализу, основанному на первой паре, P₁ и C₁:

$С_{1} = 00 \to X_{1}= 001\ или\ X_{1}= 111 \\ Если\ X_{1}= 001 \to K = X_{1} \oplus P_{1} =011. \to Если\ X_{1}= 111 \to K = X_{1} \oplus P_{1} = 101$

Используя пару P₂ и C₂, получим

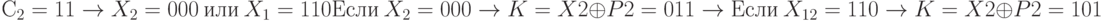
$С_{2} = 11 \to X_{2} = 000\ или\ X_{1} = 110 \\ Если\ X_{2} = 000 \to K = X2 \oplus P2 = 011 \to Если\ X_{12} = 110 \to K = X2 \oplus P2 = 101$

Два испытания показывают, что K = 011 или K =101. Хотя Ева не уверена, какое из них точное значение ключа, она знает, что самый правый бит — 1 (общий бит между двумя значениями). Продолжая атаку, можно учитывать, что самый правый бит в ключе – 1. Таким образом можно определить другие биты в этом ключе.

Общая процедура. Современные блочные шифры имеют большую сложность, чем, та, которую мы обсуждали в этом разделе. Кроме того, они могут содержать различное количество раундов. Ева может использовать следующую стратегию:

Поскольку каждый раунд содержит одни и те же операции, Ева может создать таблицу дифференциальных распределений (профайл ИСКЛЮЧАЮЩЕГО ИЛИ) для каждого S -блока и комбинировать их, чтобы создать распределение для каждого раунда.
Предположим, что каждый раунд независим (справедливое предположение). Ева может создать таблицу распределения для всего шифра, умножая соответствующие вероятности.
Ева может теперь делать список исходных текстов для атак, основанных на таблице распределений на втором шаге. Заметим, что таблица в шаге 2 только помогает Еве выбирать меньшее количество пар "исходный текст / зашифрованный текст"
Ева выбирает зашифрованный текст и находит соответствующий исходный текст. Затем она анализирует результат, чтобы найти некоторые биты в ключе.
Ева повторяет шаг 4, чтобы найти больше битов в ключе.
После нахождения достаточного количества битов в ключе Ева может использовать атаку грубой силы, чтобы найти весь ключ.

Дифференциальный криптоанализ базируется на таблице неоднородных дифференциальных распределений, S -блоков в блочном шифре.

Более детально дифференциальный криптоанализ приводится в Приложении N.

Линейный криптоанализ

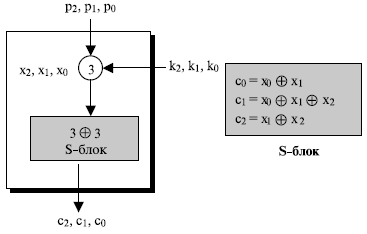
Линейный криптоанализ был представлен Митцури Мацуи (Mitsuru Matsui) в 1993 году. Анализ использует атаки знания исходного текста (в отличии от атак с выборкой исходного текста в дифференциальном криптоанализе). Полное обсуждение этой атаки базируется на некоторых понятиях теории вероятностей, которые находятся за рамками этой книги. Чтобы рассмотреть главную идею этой атаки, предположим, что шифр состоит из одного раунда, как показано на рис. 7.20, где c₀,с₁ и c₂ представляют три бита на выходе и x_Q, x₁ и x₂ представляют три бита на входе S -блока.

S -блок — линейное преобразование, в котором каждый вывод является линейной функцией ввода, как мы обсуждали ранее в этой лекции. С этим линейным компонентом мы можем создать три линейных уравнения между исходным текстом и битами зашифрованного текста, как показано ниже:

Рис. 7.20. Простой шифр с линейным S-блоком

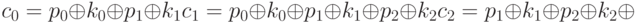
$c_{0} = p_{0} \oplus k_{0} \oplus p_{1} \oplus k_{1} \\ c_{1} = p_{0} \oplus k_{0} \oplus p_{1} \oplus k_{1} \oplus p_{2} \oplus k_{2} \\ c_{2} = p_{1} \oplus k_{1} \oplus p_{2} \oplus k_{2} \oplus$

Решая систему уравнений для трех неизвестных, мы получаем

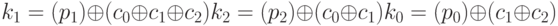
$k_{1} = (p_{1}) \oplus (c_{0} \oplus c_{1} \oplus c_{2}) \\ k_{2} = (p_{2}) \oplus (c_{0} \oplus c_{1}) \\ k_{0} = (p_{0}) \oplus (c_{1} \oplus c_{2})$

Это означает, что три атаки типа "знания исходного текста" могут найти значения k₁, и k₂. Однако реальные блочные шифры не так просты, как этот; они имеют больше компонентов, и S -блоки не линейны.

Линейная аппроксимация. В некоторых современных блочных шифрах может случиться, что некоторые S -блоки не полностью нелинейные; тогда они могут быть в вероятностном смысле аппроксимированы некоторыми линейными функциями. Вообще, задавая исходный и зашифрованный текст в n бит и ключ m бит, мы ищем некоторые уравнения, имеющие вид

$(k_{0} \oplus k_{1} \oplus \dots \oplus k_{x}) = (p_{0} \oplus p_{1} \oplus \dots \oplus p_{y}) \oplus (c_{0} \oplus c_{1} \oplus \dots \oplus c_{z})$

Дальше >>

Авторизоваться

Математика криптографии и теория шифрования

Введение в основы современных шифров с симметричным ключом

Атаки на блочные шифры

Дифференциальный криптоанализ

Линейный криптоанализ

Вопросы и ответы