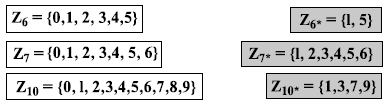|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Модульная арифметика
Инверсии
Когда мы работаем в модульной арифметике, нам часто нужно найти операцию, которая позволяет вычислить величину, обратную заданному числу. Мы обычно ищем аддитивную инверсию (оператор, обратный сложению) или мультипликативную инверсию (оператор, обратный умножению).
Аддитивная инверсия
В Zn два числа a и b аддитивно инверсны друг другу, если b = n – a. Например,
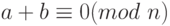
В Zn аддитивная инверсия числу a может быть вычислена как b = n – a. Например, аддитивная инверсия 4 в Z10 равна 10 – 4 = 6.
Обратите внимание, что в модульной арифметике каждое число имеет аддитивную инверсию, и эта инверсия уникальна; каждое число имеет одну и только одну аддитивную инверсию. Однако инверсия числа может быть непосредственно тем же самым числом.
Пример 2.21
Найдите все взаимно обратные пары по сложению в Z10.
Решение
Даны шесть пар аддитивных инверсий — (0, 0), (1, 9), (2, 8), (3, 7), (4, 6) и (5, 5). В этом списке 0 — инверсия самому себе; так же и 5. Обратите внимание: аддитивные инверсии обратны друг другу; если 4 — аддитивная инверсия 6, тогда 6 — также аддитивная инверсия числу 4.
Мультипликативная инверсия
В Zn два числа a и b мультипликативно инверсны друг другу, если
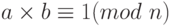
Например, если модуль равен 10, то мультипликативная инверсия 3 есть 7. Другими словами, мы имеем  .
.
Может быть доказано, что a имеет мультипликативную инверсию в Zn, если только НОД(n, a) = 1. В этом случае говорят, что a и n взаимно простые.
Пример 2.22
Найти мультипликативную инверсию 8 в Z10.
Решение
Мультипликативная инверсия не существует, потому что 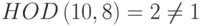 . Другими словами, мы не можем найти число между 0 и 9, такое, что при умножении на 8 результат сравним с 1 по mod 10.
. Другими словами, мы не можем найти число между 0 и 9, такое, что при умножении на 8 результат сравним с 1 по mod 10.
Пример 2.23
Найти все мультипликативные инверсии в Z10.
Решение
Есть только три пары, удовлетворяющие условиям существования мультипликативной инверсии: (1, 1), (3, 7) и (9, 9). Числа 0, 2, 4, 5, 6 и 8 не имеют мультипликативной инверсии.
Мы можем проверить, что
(1 x 1) mod 10 = 1 (3 x 7) mod 10 = 1 (9 x 9) mod 10 = 1
Пример 2.24
Найти все мультипликативные обратные пары в Z11.
Решение
Мы имеем следующие пары: (1, 1), (2, 6), (3, 4), (5, 9), (7, 8) и (10, 10). При переходе от Z10 к Z11 число пар увеличивается. При Z11 НОД (11, a) = 1 (взаимно простые) для всех значений a, кроме 0. Это означает, что все целые числа от 1 до 10 имеют мультипликативные инверсии.
Расширенный алгоритм Евклида, который мы обсуждали ранее в этой лекции, может найти мультипликативную инверсию b в Zn, когда даны n и b и инверсия существует. Для этого нам надо заменить первое целое число a на n (модуль). Далее мы можем утверждать, что алгоритм может найти s и t, такие, что 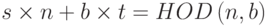 . Однако если мультипликативная инверсия b существует, НОД (n, b) должен быть 1. Так что уравнение будет иметь вид
. Однако если мультипликативная инверсия b существует, НОД (n, b) должен быть 1. Так что уравнение будет иметь вид
Теперь мы применяем операции по модулю к обеим сторонам уравнения. Другими словами, мы отображаем каждую сторону к Zn. Тогда мы будем иметь
(s x n + b x t) mod n =1 mod n [(s x n) mod n] + [(b x t) mod n] = 1 mod n 0 + [(b x t) mod n ] = 1 (b x t) mod n =1 -> Это означает, что t – это мультипликативная инверсия b в Zn
Обратите внимание, что ![[(s \times n)\bmod n]](/sites/default/files/tex_cache/7e3ed054c02628543298573ecfaa9fd3.png) на третьей строке — 0, потому что, если мы делим
на третьей строке — 0, потому что, если мы делим 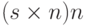 , частное — s, а остаток — 0.
, частное — s, а остаток — 0.
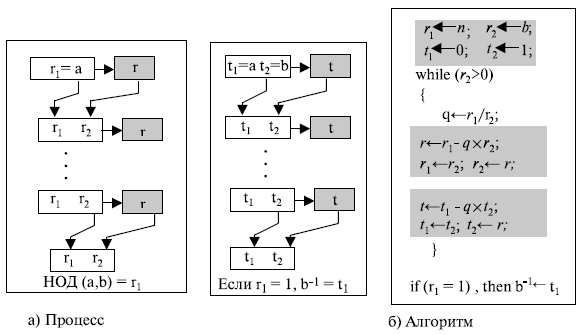
Рисунок 2.15 показывает, как мы находим мультипликативную инверсию числа, используя расширенный алгоритм Евклида.
Пример 2.25
Найти мультипликативную инверсию 11 в Z26.
Решение
Мы используем таблицу, аналогичную одной из тех, которые мы уже применяли прежде при данных r1 = 26 и r2 = 11. Нас интересует только значение t.
НОД (26, 11) = 1, что означает, что мультипликативная инверсия 11 существует. Расширенный алгоритм Евклида дает t1 = (–7).
Мультипликативная инверсия равна (–7) mod 26 = 19. Другими словами, 11 и 19 — мультипликативная инверсия в Z26. Мы можем видеть, что 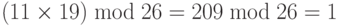 .
.
Пример 2.26
Найти мультипликативную инверсию 23 в Z100.
Решение
Мы используем таблицу, подобную той, которую применяли до этого при r1 = 100 и r2 = 23. Нас интересует только значение t.
НОД (100, 23) = 1, что означает, что инверсия 23 существует. Расширенный Евклидов алгоритм дает t1 =-13. Инверсия — (–13) mod 100 = 87. Другими словами, 13 и 87 — мультипликативные инверсии в Z100. Мы можем видеть, что 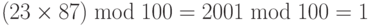 .
.
Пример 2.27
Найти мультипликативную инверсию 12 в Z26.
Решение
Мы используем таблицу, подобную той, которую мы применяли раньше при r1 = 26 и r2 = 12.
 , что означает отсутвствие для числа 12 мультипликативной инверсии в Z26
, что означает отсутвствие для числа 12 мультипликативной инверсии в Z26
Сложение и умножение таблиц
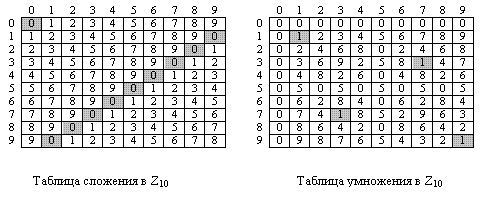
Рисунок 2.16 показывает две таблицы для сложения и умножения. При сложении таблиц каждое целое число имеет аддитивную инверсию. Обратные пары могут быть найдены, если результат их сложения — ноль. Мы имеем (0, 0), (1, 9), (2, 8), (3, 7), (4, 6) и (5, 5). При умножении таблиц мы получаем только три мультипликативных пары (1, 1), (3, 7) и (9, 9). Пары могут быть найдены, когда результат умножения равен 1. Обе таблицы симметричны по диагонали, от левой вершины к нижней вершине справа. При этом можно обнаружить свойства коммутативности для сложения и умножения ( a+b = b+a и  ). Таблица сложения также показывает, что каждый ряд или колонка может поменяться с другим рядом или колонкой. Для таблицы умножения это неверно.
). Таблица сложения также показывает, что каждый ряд или колонка может поменяться с другим рядом или колонкой. Для таблицы умножения это неверно.
Различные множества для сложения и умножения
В криптографии мы часто работаем с инверсиями. Если отправитель посылает целое число (например, ключ для шифрования слова), приемник применяет инверсию этого целого числа (например, ключ декодирования). Если это действие (алгоритм шифрования/декодирования) является сложением, множество Zn может быть использовано как множество возможных ключей, потому что каждое целое число в этом множестве имеет аддитивную инверсию. С другой стороны, если действие (алгоритм шифрования/декодирования) — умножение, Zn не может быть множеством возможных ключей, потому что только некоторые члены этого множества имеют мультипликативную инверсию. Нам нужно другое множество, которое является подмножеством Zn и включает в себя только целые числа, и при этом в Zn они имеют уникальную мультипликативную инверсию. Это множество обозначается Zn*. Рисунок 2.17 показывает некоторые случаи двух множеств. Обратите внимание, что множество Zn* может быть получено из таблицы умножения типа показанной на рис. 2.16.
Каждый член Zn имеет аддитивную инверсию, но только некоторые члены имеют мультипликативную инверсию. Каждый член Zn* имеет мультипликативную инверсию, но только некоторые члены множества имеют аддитивную инверсию.
Еще два множества
Криптография часто использует еще два множества: Zp, и Zp*. Модули в этих двух множествах — простые числа. Простые числа будут обсуждаться в следующих лекциях; пока можно сказать, что простое число имеет только два делителя: целое число 1 и само себя.
Множество Zp — то же самое, что и Zn, за исключением того, что n — простое число. Zp содержит все целые числа от 0 до p – 1. Каждый элемент в Zp имеет аддитивную инверсию; каждый элемент кроме 0 имеет мультипликативную инверсию.
Множество Zp* — то же самое, что Zn*, за исключением того, что Zp* содержит все целые числа от 1 до p – 1. Каждый элемент в Zp имеет аддитивную и мультипликативную инверсии. Zp* очень хороший кандидат, когда мы нуждаемся во множестве, которое поддерживает аддитивную и мультипликативную инверсии.
Ниже показаны два множества, когда p = 13.
Z13 = {0,1,2,3,4,5,6,7,8,9,10,11,12},
Z13* = {1,2,3,4,5,6,7,8,9,10,11,12},