Проектирование реляционных баз данных на основе принципов нормализации: первые шаги нормализации

Нетранзитивные функциональные зависимости и третья нормальная форма

В произведенной декомпозиции переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ_ЗАДАНИЯ множество FD переменной отношения СЛУЖ_ПРО_ЗАДАН предельно просто – в единственной нетривиальной функциональной зависимости детерминантом является возможный ключ. При использовании этой переменной отношения какие-либо аномалии обновления не возникают. Однако переменная отношения СЛУЖ не является такой же совершенной.

Аномалии обновлений, возникающие из-за наличия транзитивных функциональных зависимостей

Функциональные зависимости переменной отношения СЛУЖ по-прежнему порождают некоторые аномалии обновления. Они вызываются наличием транзитивной FD СЛУ_НОМ->СЛУ_ЗАРП (через FD СЛУ_НОМ->СЛУ_УРОВ и СЛУ_УРОВ->СЛУ_ЗАРП ). Эти аномалии связаны с избыточностью хранения значения атрибута СЛУ_ЗАРП в каждом кортеже, характеризующем служащих с одним и тем же разрядом.

• Добавление кортежей. Невозможно сохранить данные о новом разряде (и соответствующем ему размере зарплаты), пока не появится служащий с новым разрядом. (Первичный ключ не может содержать неопределенные значения.)
• Удаление кортежей. При увольнении последнего служащего с данным разрядом мы утратим информацию о наличии такого разряда и соответствующем размере зарплаты.
• Модификация кортежей. При изменении размера зарплаты, соответствующей некоторому разряду, мы будем вынуждены изменить значение атрибута СЛУ_ЗАРП в кортежах всех служащих, которым назначен этот разряд (иначе не будет выполняться FD СЛУ_УРОВ->СЛУ_ЗАРП ).

Возможная декомпозиция

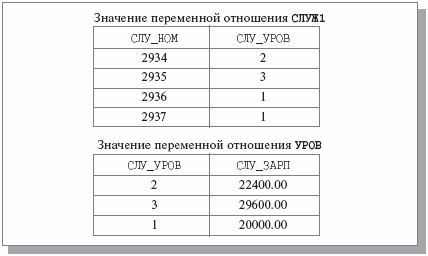
Для преодоления этих трудностей произведем декомпозицию переменной отношения СЛУЖ на две переменных отношений – СЛУЖ1 {СЛУ_НОМ, СЛУ_УРОВ} и УРОВ {СЛУ_УРОВ, СЛУ_ЗАРП}. По теореме Хита, это снова декомпозиция без потерь по причине наличия, например, FD СЛУ_НОМ->СЛУ_УРОВ. На рис. 7.5 показаны диаграммы FD этих переменных отношений, а на рис. 7.6 – их возможные значения.

Рис. 7.5. Диаграммы FD в отношениях СЛУЖ1 и УРОВ

Как видно из рис. 7.6, это преобразование обратимо, т. е. любое допустимое значение исходной переменной отношения СЛУЖ является естественным соединением значений отношений СЛУЖ1 и УРОВ. Также можно заметить, что мы избавились от трудностей при выполнении операций обновления.

• Добавление кортежей. Чтобы сохранить данные о новом разряде, достаточно добавить соответствующий кортеж к отношению УРОВ.
• Удаление кортежей. При увольнении последнего служащего, обладающего данным разрядом, удаляется соответствующий кортеж из отношения СЛУЖ1, и данные о разряде сохраняются в отношении УРОВ.
• Модификация кортежей. При изменении размера зарплаты, соответствующей некоторому разряду, изменяется значение атрибута СЛУ_ЗАРП ровно в одном кортеже отношения УРОВ.

Третья нормальная форма

Рис. 7.6. Тела отношений СЛУЖ1 и УРОВ

Трудности, которые мы испытывали, были связаны с наличием транзитивной FD СЛУ_НОМ->СЛУ_ЗАРП. Наличие этой FD на самом деле означало, что атрибут СЛУ_ЗАРП характеризовал не сущность служащий, а сущность разряд.

Переменная отношения находится в третьей нормальной форме (3NF) в том и только в том случае, когда она находится во второй нормальной форме, и каждый неключевой атрибут нетранзитивно^{4Очевидно, что FD называется нетранзитивной тогда и только тогда, когда она не является транзитивной.} функционально зависит от первичного ключа^{5В этом определении опять предполагается, что у отношения имеется только один возможный ключ.} .

Отношения СЛУЖ1 и УРОВ оба находятся в 3NF (все неключевые атрибуты нетранзитивно зависят от первичных ключей СЛУ_НОМ и СЛУ_УРОВ ). Отношение СЛУЖ не находится в 3NF (FD СЛУ_НОМ->СЛУ_ЗАРП является транзитивной). Любое отношение, находящееся в 2NF, но не находящееся в 3NF, может быть приведено к набору отношений, находящихся в 3NF. Мы получаем набор проекций исходного отношения, естественное соединение которых воспроизводит исходное отношение (т. е. это декомпозиция без потерь). Для отношений СЛУЖ1 и УРОВ исходное отношение СЛУЖ воспроизводится их естественным соединением по общему атрибуту СЛУ_УРОВ.

Заметим, что допустимые значения отношения УРОВ могут содержать кортежи, информационное наполнение которых выходит за пределы тела отношения СЛУЖ. Например, в теле отношения УРОВ может находиться кортеж с данными о разряде 4, который еще не присвоен ни одному служащему. Наличие такого кортежа не влияет на результат естественного соединения, который все равно будет являться допустимым значением отношения СЛУЖ.

Независимые проекции отношений. Теорема Риссанена

Обратите внимание, что для переменной отношения СЛУЖ {СЛУ_НОМ, СЛУ_УРОВ, СЛУ_ЗАРП}, кроме декомпозиции на отношения СЛУЖ1 {СЛУ_НОМ, СЛУ_УРОВ} и УРОВ {СЛУ_УРОВ, СЛУ_ЗАРП}, возможна и декомпозиция на отношения СЛУЖ1 {СЛУ_НОМ, СЛУ_УРОВ} и СЛУЖ_ЗАРП {СЛУ_НОМ, СЛУ_ЗАРП}^{6Теоретически возможная третья декомпозиция отношения СЛУЖ на отношения СЛУЖ2 {СЛУ_НОМ, СЛУ_ЗАРП} и УРОВ {СЛУ_УРОВ, СЛУ_ЗАРП} не является декомпозицией без потерь. Чтобы убедиться в этом, рассмотрите случай, когда для двух разных разрядов сотрудников назначен один и тот же размер зарплаты. Покажите также, что для этой декомпозиции не выполняются условия теоремы Хита.} . Оба отношения, полученные путем второй декомпозиции, находятся в 3NF, и эта декомпозиция также является декомпозицией без потерь. Тем не менее вторая декомпозиция, в отличие от первой, не устраняет проблемы, связанные с обновлением отношения СЛУЖ. Например, по-прежнему невозможно сохранить данные о разряде, которым не обладает ни один служащий. Посмотрим, с чем это связано.

Отношения СЛУЖ1 и УРОВ могут обновляться независимо (являются независимыми проекциями ), и при этом результат их естественного соединения всегда будет таким, как если бы обновлялось исходное отношение СЛУЖ. Это происходит потому, что FD отношения СЛУЖ трансформировались в индивидуальные ограничения первичного ключа отношений СЛУЖ1 и УРОВ. При второй декомпозиции FD СЛУ_УРОВ->СЛУ_ЗАРП трансформируется в ограничение целостности сразу для двух отношений (такого рода ограничения целостности называются ограничениями базы данных, и их поддержка гораздо более накладна с технической точки зрения). Понятно, что в процессе нормализации декомпозиция отношения на независимые проекции является предпочтительной. Необходимые и достаточные условия независимости проекций отношения обеспечивает теорема Риссанена.

Теорема Риссанена

Проекции r1 и r2 отношения r являются независимыми тогда и только тогда, когда:

• каждая FD в отношении r логически следует^{7Т.е. выводится на основе аксиом Армстронга.} из FD в r1 и r2 ;
• общие атрибуты r1 и r2 образуют возможный ключ хотя бы для одного из этих отношений.

Мы не будем приводить доказательство этой теоремы, но продемонстрируем ее верность на примере двух показанных выше декомпозиций отношения СЛУЖ. В первой декомпозиции (на проекции СЛУЖ1 и УРОВ ) общий атрибут СЛУ_УРОВ является возможным (и первичным) ключом отношения УРОВ, а единственная дополнительная FD отношения СЛУЖ (СЛУ_НОМ->СЛУ_ЗАРП) логически следует из FD СЛУ_НОМ->СЛУ_УРОВ и СЛУ_УРОВ->СЛУ_ЗАРП, выполняемых для отношений СЛУЖ1 и УРОВ соответственно. Вторая декомпозиция удовлетворяет второму условию теоремы Риссанена ( СЛУ_НОМ является первичным ключом в каждом из отношений СЛУЖ1 и СЛУ_ЗАРП ), но FD СЛУ_УРОВ->СЛУ_ЗАРП не выводится из FD СЛУ_НОМ->СЛУ_УРОВ и СЛУ_НОМ->СЛУ_ЗАРП.

Атомарным отношением называется отношение, которое невозможно декомпозировать на независимые проекции . Далеко не всегда для неатомарных (не являющихся атомарными ) отношений требуется декомпозиция на атомарные проекции. Например, отношение СЛУЖ2 {СЛУ_НОМ, СЛУ_ЗАРП, ПРО_НОМ} с множеством FD {СЛУ_НОМ->СЛУ_ЗАРП, СЛУ_НОМ->ПРО_НОМ} не является атомарным (возможна декомпозиция на независимые проекции СЛУЖ3 {СЛУ_НОМ, СЛУ_ЗАРП} и СЛУЖ4 {СЛУ_НОМ, ПРО_НОМ} ). Но эта декомпозиция не улучшает свойства отношения СЛУЖ2 и поэтому не является осмысленной. Другими словами, при выборе способа декомпозиции нужно стремиться к получению независимых проекций, но не обязательно атомарных.