НОУ ИНТУИТ | Структуры и алгоритмы компьютерной обработки данных. Лекция 41: Алгоритмы поиска на основе деревьев

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 02.02.2011 | Уровень: для всех | Доступ: свободно

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать программу

Оптимальные деревья

В двоичном дереве поиск одних элементов может происходить чаще, чем других, то есть существуют вероятности p_k поиска k -го элемента и для различных элементов эти вероятности неодинаковы. Можно предположить, что поиск в дереве в среднем будет более быстрым, если те элементы, которые ищут чаще, будут находиться ближе к корню дерева.

Пусть даны 2n+1 вероятностей p₁,p₂,...,p_n, q₀,q₁,...,q_n, где p_i – вероятность того, что аргументом поиска является K_i элемент; q_i – вероятность того, что аргумент поиска лежит между вершинами K_i и K_i+1 ; q₀ – вероятность того, что аргумент поиска меньше, чем значение элемента K₁ ; q_n – вероятность того, что аргумент поиска больше, чем K_n. Тогда цена дерева поиска C будет определяться следующим образом:

$C=\sum_{j=1}^n p_j(\text{levelroot}_j+1)+\sum_{k=1}^n q_k(\text{levellist}_k),$

где $\text{levelroot}_j$ – уровень узла j, а $\text{levellist}_k$ – уровень листа K.

Дерево поиска называется оптимальным, если его цена минимальна. То есть оптимальное бинарное дерево поиска – это бинарное дерево поиска, построенное в расчете на обеспечение максимальной производительности при заданном распределении вероятностей поиска требуемых данных.

Существует подход построения оптимальных деревьев поиска, при котором элементы вставляются в порядке уменьшения частот, что дает в среднем неплохие деревья поиска. Однако этот подход может дать вырожденное дерево поиска, которое будет далеко от оптимального. Еще один подход состоит в выборе корня k таким образом, чтобы максимальная сумма вероятностей для вершин левого поддерева или правого поддерева была настолько мала, насколько это возможно. Такой подход также может оказаться плохим в случае выбора в качестве корня элемента с малым значением p_k.

Существуют алгоритмы, которые позволяют построить оптимальное дерево поиска. К ним относится, например, алгоритм Гарсия-Воча. Однако такие алгоритмы имеют временную сложность порядка O(n²). Таким образом, создание оптимальных деревьев поиска требует больших накладных затрат, что не всегда оправдывает выигрыш при быстром поиске.

Сбалансированные по высоте деревья

В худшем случае, когда дерево вырождено в линейный список, хранение данных в упорядоченном бинарном дереве никакого выигрыша в сложности операций по сравнению с массивом или линейным списком не дает. В лучшем случае, когда дерево сбалансировано, для всех операций получается логарифмическая сложность, что гораздо лучше. Идеально сбалансированным называется дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более чем на 1.

Однако идеальную сбалансированность довольно трудно поддерживать. В некоторых случаях при добавлении или удалении элементов может потребоваться значительная перестройка дерева, не гарантирующая логарифмической сложности. В 1962 году два советских математика: Г.М. Адельсон-Вельский и Е.М. Ландис – ввели менее строгое определение сбалансированности и доказали, что при таком определении можно написать программы добавления и/или удаления, имеющие логарифмическую сложность и сохраняющие дерево сбалансированным. Дерево считается сбалансированным по АВЛ (сокращения от фамилий Г.М. Адельсон-Вельский и Е.М. Ландис), если для каждой вершины выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1. Не всякое сбалансированное по АВЛ дерево идеально сбалансировано, но всякое идеально сбалансированное дерево сбалансировано по АВЛ.

При операциях добавления и удаления может произойти нарушение сбалансированности дерева. В этом случае потребуются некоторые преобразования, не нарушающие упорядоченности дерева и способствующие лучшей сбалансированности.

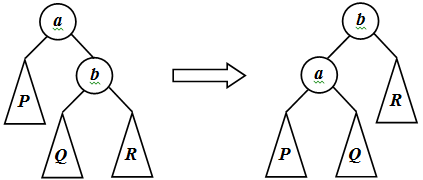
Рассмотрим такие преобразования. Пусть вершина a имеет правый потомок b. Обозначим через P левое поддерево вершины a, через Q и R – левое и правое поддеревья вершины b соответственно. Упорядоченность дерева требует, чтобы P<a<Q<b<R. Точно того же требует упорядоченность дерева с корнем b, его левым потомком a, в котором P и Q – левое и правое поддеревья вершины a, R – правое поддерево вершины b. Поэтому первое дерево можно преобразовать во второе, не нарушая упорядоченности. Такое преобразование называется малым правым вращением ( рис. 40.3). Аналогично определяется симметричное ему малое левое вращение.

Рис. 40.3. Малое правое вращение АВЛ-дерева

Пусть b – правый потомок вершины a, c – левый потомок вершины b, P – левое поддерево вершины a, Q и R – соответственно левое и правое поддеревья вершины c, S – правое поддерево b. Тогда P<a<Q<c<R<b<S. Такой же порядок соответствует дереву с корнем c, имеющим левый потомок a и правый потомок b, для которых P и Q – поддеревья вершины a, а R и S – поддеревья вершины b. Соответствующее преобразование будем называть большим правым вращением ( рис. 40.4). Аналогично определяется симметричное ему большое левое вращение.

Рис. 40.4. Большое правое вращение АВЛ-дерева

Схематично алгоритм добавления нового элемента в сбалансированное по АВЛ дерево будет состоять из следующих трех основных шагов.

Шаг 1. Поиск по дереву.

Шаг 2. Вставка элемента в место, где закончился поиск, если элемент отсутствует.

Шаг 3. Восстановление сбалансированности.

Первый шаг необходим для того, чтобы убедиться в отсутствии элемента в дереве, а также найти такое место вставки, чтобы после вставки дерево осталось упорядоченным. Третий шаг представляет собой обратный проход по пути поиска: от места добавления к корню дерева. По мере продвижения по этому пути корректируются показатели сбалансированности проходимых вершин, и производится балансировка там, где это необходимо. Добавление элемента в дерево никогда не требует более одного поворота.

#include "stdafx.h"
#include <iostream>
#include <time.h>
using namespace std;
typedef int ElementType;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;
struct AvlNode {
            ElementType Element;
            AvlTree Left;
            AvlTree Right;
            int Height;
        };

AvlTree MakeEmpty( AvlTree T );
Position Find( ElementType X, AvlTree T );
Position FindMin( AvlTree T );
Position FindMax( AvlTree T );
AvlTree Insert( ElementType X, AvlTree T );
ElementType Retrieve( Position P );
void printTree(AvlTree T, int l = 0);

int _tmain(int argc, _TCHAR* argv[]){
  int i, *a, maxnum;
  AvlTree T;
    Position P;
    int j = 0;
  cout << "Введите количество элементов maxnum : ";
  cin >> maxnum;
  cout << endl;
    a = new int[maxnum];
  srand(time(NULL)*1000);
  // генерация массива
  for (i = 0; i < maxnum; i++)
    a[i] = rand()%100;
  cout << "Вывод сгенерированной последовательности" << endl;
  for (i = 0; i < maxnum; i++)
    cout << a[i] << " ";
  cout << endl;
  cout << endl;
  // добавление элементов в АВЛ-дерево
    T = MakeEmpty( NULL );
  for( i = 0; i < maxnum; i++ )
        T = Insert( a[i], T );
  cout << "Вывод АВЛ-дерева" << endl;
  printTree(T);
  cout << endl;
  cout << "Min = " << Retrieve( FindMin( T ) ) << ", Max = " 
       << Retrieve( FindMax( T ) ) << endl;
  // удаление АВЛ-дерева
  T = MakeEmpty(T);
  delete [] a;
  system("pause");
  return 0;
}

//функция удаления вершины и его поддеревьев
AvlTree MakeEmpty( AvlTree T ) {
  if( T != NULL ){
    MakeEmpty( T->Left );
    MakeEmpty( T->Right );
    free( T );
  }
  return NULL;
}

// поиск вершины со значением X
Position Find( ElementType X, AvlTree T ) {
  if( T == NULL )
    return NULL;
    if( X < T->Element )
      return Find( X, T->Left );
    else
      if( X > T->Element )
        return Find( X, T->Right );
      else
        return T;
}

//функция поиска вершины с минимальным значением
Position FindMin( AvlTree T ) {
  if( T == NULL )
    return NULL;
  else
    if( T->Left == NULL )
      return T;
    else
      return FindMin( T->Left );
}

//функция поиска вершины с максимальным значением
Position FindMax( AvlTree T ) {
  if( T != NULL )
    while( T->Right != NULL )
      T = T->Right;
  return T;
}

//функция возвращает вес вершины
static int Height( Position P ) {
  if( P == NULL )
    return -1;
  else
    return P->Height;
}

//функция возвращает максимальное из двух чисел
static int Max( int Lhs, int Rhs ) {
  return Lhs > Rhs ? Lhs : Rhs;
}

/*функция выполняет поворот между вершинами K2 и его левым потомком*/
static Position SingleRotateWithLeft( Position K2 ) {
  Position K1;
  K1 = K2->Left;
  K2->Left = K1->Right;
  K1->Right = K2;
  K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;
  K1->Height = Max( Height( K1->Left ), K2->Height ) + 1;
  return K1;  //Новый корень
}

//функция выполняет поворот между вершинами K1 и его правым потомком
static Position SingleRotateWithRight( Position K1 ) {
  Position K2;
  K2 = K1->Right;
  K1->Right = K2->Left;
  K2->Left = K1;
  K1->Height = Max(Height(K1->Left), Height(K1->Right)) + 1;
  K2->Height = Max( Height( K2->Right ), K1->Height ) + 1;
  return K2;  //новый корень
}

//функция выполняет двойной левый-правый поворот
static Position DoubleRotateWithLeft( Position K3 ) {
  // поворот между K1 и K2/
  K3->Left = SingleRotateWithRight( K3->Left );
  // поворот между K3 и K2
  return SingleRotateWithLeft( K3 );
}

//функция выполняет двойной правый-левый поворот
static Position DoubleRotateWithRight( Position K1 ) {
  // поворот между K3 и K2
  K1->Right = SingleRotateWithLeft( K1->Right );
  // поворот между K1 и K2
  return SingleRotateWithRight( K1 );
}

//функция вставки вершины в АВЛ-дерево
AvlTree Insert( ElementType X, AvlTree T ){
  if( T == NULL ){
    T = new AvlNode();
    if( T == NULL )
      fprintf( stderr, "Недостаточно памяти!!!\n" );
    else {
      T->Element = X; T->Height = 0;
      T->Left = T->Right = NULL;
    }
  }
  else if( X < T->Element ) {
    T->Left = Insert( X, T->Left );
    if( Height( T->Left ) - Height( T->Right ) == 2 )
      if( X < T->Left->Element )
        T = SingleRotateWithLeft( T );
      else
        T = DoubleRotateWithLeft( T );
  }
  else if( X > T->Element ) {
    T->Right = Insert( X, T->Right );
      if( Height( T->Right ) - Height( T->Left ) == 2 )
        if( X > T->Right->Element )
          T = SingleRotateWithRight( T );
        else
          T = DoubleRotateWithRight( T );
  }
  T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
  return T;
}

//функция возвращает значение, хранящееся в вершине
ElementType Retrieve( Position P ) {
  return P->Element;
}

//функция вывода АВЛ-дерева на печать
void printTree(AvlTree T, int l){
  int i;
  if ( T != NULL ) {
    printTree(T->Right, l+1);
    for (i=0; i < l; i++) cout << "    ";
    printf ("%4ld", Retrieve ( T ));
    printTree(T->Left, l+1);
  }
  else cout << endl;
}

Листинг .

Алгоритм удаления элемента из сбалансированного дерева будет выглядеть так:

Шаг 1. Поиск по дереву.

Шаг 2. Удаление элемента из дерева.

Шаг 3. Восстановление сбалансированности дерева (обратный проход).

Первый шаг необходим, чтобы найти в дереве вершину, которая должна быть удалена. Третий шаг представляет собой обратный проход от места, из которого взят элемент для замены удаляемого, или от места, из которого удален элемент, если в замене не было необходимости. Операция удаления может потребовать перебалансировки всех вершин вдоль обратного пути к корню дерева, т.е. порядка log n вершин. Таким образом, алгоритмы поиска, добавления и удаления элементов в сбалансированном по АВЛ дереве имеют сложность, пропорциональную O(log n).

Деревья цифрового (поразрядного) поиска

Методы цифрового поиска достаточно громоздки и плохо иллюстрируются. Рассмотрим бинарное дерево цифрового поиска. Как и в деревьях, рассмотренных выше, в каждой вершине такого дерева хранится полный ключ, но переход по левой или правой ветви происходит не путем сравнения ключа-эталона со значением ключа, хранящегося в вершине, а на основе значения очередного бита аргумента. Реализация цифрового поиска происходит поразрядно (побитово).

Поиск начинается от корня дерева. Если содержащийся в корневой вершине ключ не совпадает с аргументом поиска, то анализируется самый левый бит аргумента. Если он равен 0, происходит переход по левой ветви, если 1 – по правой. Если не обнаруживается совпадение ключа с аргументом поиска, то анализируется следующий бит аргумента и т.д. Поиск завершается, когда будут проверены все биты аргумента либо встретится вершина с отсутствующей левой или правой ссылкой.

Ключевые термины

Бинарное дерево цифрового поиска – это дерево, в каждой вершине которого хранится полный ключ, а переход по ветвям происходит на основе значения очередного бита аргумента.

Двоичное (бинарное) дерево – это иерархическая структура, в которой каждый узел имеет не более двух потомков.

Идеально сбалансированное дерево – это дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более чем на 1.

Ключ поиска – это поле, по значению которого происходит поиск.

Оптимальное бинарное дерево поиска – это бинарное дерево поиска, построенное в расчете на обеспечение максимальной производительности при заданном распределении вероятностей поиска требуемых данных.

Поиск – это процесс нахождения конкретной информации в ранее созданном множестве данных.

Сбалансированное по АВЛ дерево – это дерево, для каждой вершины которого выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1.

Случайные деревья поиска – это упорядоченные бинарные деревья поиска, при создании которых элементы вставляются в случайном порядке.

Упорядоченное двоичное дерево – это двоичное дерево, в котором для любой его вершины x справедливы свойства: все элементы в левом поддереве меньше элемента, хранимого в x ; все элементы в правом поддереве больше элемента, хранимого в x ; все элементы дерева различны.

Частично упорядоченное бинарное дерево – это упорядоченное бинарное дерево, в котором встречаются одинаковые элементы.

Поиск данных предполагает использование соответствующих алгоритмов в зависимости от ряда факторов: способ представления данных, упорядоченность множества поиска, объем данных, расположение их во внешней или во внутренней памяти.
Двоичные деревья представляют собой иерархическую структуру, в которой каждый узел имеет не более двух потомков. Поиск на двоичных деревьях не дает выигрыша по времени по сравнению с линейными структурами.
Упорядоченное двоичное дерево – это двоичное дерево, в котором для любой его вершины x справедливы свойства: все элементы в левом поддереве меньше элемента, хранимого в x ; все элементы в правом поддереве больше элемента, хранимого в x ; все элементы дерева различны. Поиск в худшем случае на таких деревьях имеет сложность O(n).
Случайные деревья поиска представляют собой упорядоченные бинарные деревья поиска, при создании которых элементы (их ключи) вставляются в случайном порядке. Высота дерева зависит от случайного поступления элементов, поэтому трудоемкость определяется построением дерева.
Оптимальное бинарное дерево поиска – это бинарное дерево поиска, построенное в расчете на обеспечение максимальной производительности при заданном распределении вероятностей поиска требуемых данных. Поиск на таких деревьях имеет сложность порядка O(n²).
Дерево считается сбалансированным по АВЛ, если для каждой вершины выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1. Алгоритмы поиска, добавления и удаления элементов в таком дереве имеют сложность, пропорциональную O(log n).
В деревьях цифрового поиска осуществляется поразрядное сравнение ключей.

Дальше >>

Структуры и алгоритмы компьютерной обработки данных