Алгоритмы поиска в тексте
Цель лекции: изучить основные алгоритмы поиска в тексте и научиться решать задачи поиска в тексте на основе алгоритмов прямого поиска; Кнута, Морриса и Пратта; Боуера и Мура.
Работа в текстовом редакторе, поисковые запросы в базе данных, задачи в биоинформатике, лексический анализ программ требуют эффективных алгоритмов работы с текстом. Задачи поиска слова в тексте используются в криптографии, различных разделах физики, сжатии данных, распознавании речи и других сферах человеческой деятельности.
Введем ряд определений, которые будут использоваться далее в изложении материала.
Алфавит – конечное множество символов.
Строка (слово) – это последовательность символов из некоторого алфавита. Длина строки – количество символов в строке.
Строку будем обозначать символами алфавита, например X=x[1]x[2]...x[n] – строка длиной n, где x[i] – i -ый символ строки Х, принадлежащий алфавиту. Строка, не содержащая ни одного символа, называется пустой.
Строка X называется подстрокой строки Y, если найдутся такие строки Z1 и Z2, что Y=Z1XZ2. При этом Z1 называют левым, а Z2 – правым крылом подстроки. Подстрокой может быть и сама строка. Иногда при этом строку X называют вхождением в строку Y. Например, строки hrf и fhr является подстроками строки abhrfhr.
Подстрока X называется префиксом строки Y, если есть такая подстрока Z, что Y=XZ. Причем сама строка является префиксом для себя самой (так как найдется нулевая строка L, что X=XL ). Например, подстрока ab является префиксом строки abcfa.
Подстрока X называется суффиксом строки Y, если есть такая подстрока Z, что Y=ZX. Аналогично, строка является суффиксом себя самой. Например, подстрока bfg является суффиксом строки vsenfbfg.
Поставим задачу поиска подстроки в строке. Пусть задана строка, состоящая из некоторого количества символов. Проверим, входит ли заданная подстрока в данную строку. Если входит, то найдем номер, начиная с какого символа строки, то есть, определим первое вхождение заданной подстроки в исходной строке.
Рассмотрим несколько известных алгоритмов поиска подстроки в строке более подробно.
Прямой поиск
Данный алгоритм еще называется алгоритмом последовательного поиска, он является самым простым и очевидным.
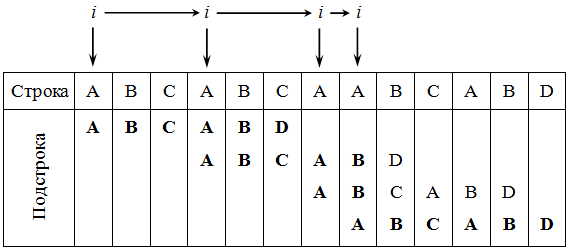
Основная идея алгоритма прямым поиском заключается в посимвольном сравнении строки с подстрокой. В начальный момент происходит сравнение первого символа строки с первым символом подстроки, второго символа строки со вторым символом подстроки и т. д. Если произошло совпадение всех символов, то фиксируется факт нахождения подстроки. В противном случае производится сдвиг подстроки на одну позицию вправо и повторяется посимвольное сравнение, то есть сравнивается второй символ строки с первым символом подстроки, третий символ строки со вторым символом подстроки и т. д. ( рис. 39.1) Символы, которые сравниваются, на рисунке выделены жирным. Рассматриваемые сдвиги подстроки повторяются до тех пор, пока конец подстроки не достиг конца строки или не произошло полное совпадение символов подстроки со строкой, то есть найдется подстрока.
//Описание функции прямого поиска подстроки в строке
int DirectSearch(char *string, char *substring){
int sl, ssl;
int res = -1;
sl = strlen(string);
ssl = strlen(substring);
if ( sl == 0 )
cout << "Неверно задана строка\n";
else if ( ssl == 0 )
cout << "Неверно задана подстрока\n";
else
for (int i = 0; i < sl - ssl + 1; i++)
for (int j = 0; j < ssl; j++)
if ( substring[j] != string[i+j] )
break;
else if ( j == ssl - 1 ){
res = i;
break;
}
return res;
}Данный алгоритм является малозатратным и не нуждается в предварительной обработке и в дополнительном пространстве. Большинство сравнений алгоритма прямого поиска являются лишними. Поэтому в худшем случае алгоритм будет малоэффективен, так как его сложность будет пропорциональна O((n-m+1)xm), где n и m – длины строки и подстроки соответственно.
Алгоритм Кнута, Морриса и Пратта
Алгоритм был открыт Д. Кнутом и В. Праттом и, независимо от них, Д. Моррисом. Результаты своей работы они совместно опубликовали в 1977 году. Алгоритм Кнута, Морриса и Пратта (КМП-алгоритм) является алгоритмом, который фактически требует только O(n) сравнений даже в самом худшем случае. Рассматриваемый алгоритм основывается на том, что после частичного совпадения начальной части подстроки с соответствующими символами строки фактически известна пройденная часть строки и можно, вычислить некоторые сведения, с помощью которых затем быстро продвинуться по строке.
Основным отличием алгоритма Кнута, Морриса и Пратта от алгоритма прямого поиска заключается в том, что сдвиг подстроки выполняется не на один символ на каждом шаге алгоритма, а на некоторое переменное количество символов. Следовательно, перед тем как осуществлять очередной сдвиг, необходимо определить величину сдвига. Для повышения эффективности алгоритма необходимо, чтобы сдвиг на каждом шаге был бы как можно большим ( рис. 39.2). На рисунке символы, подвергшиеся сравнению, выделены жирным шрифтом.
Если для произвольной подстроки определить все ее начала, одновременно являющиеся ее концами, и выбрать из них самую длинную (не считая, конечно, саму строку), то такую процедуру принято называть префикс-функцией. В реализации алгоритма Кнута, Морриса и Пратта используется предобработка искомой подстроки, которая заключается в создании префикс-функции на ее основе. При этом используется следующая идея: если префикс (он же суффикс) строки длиной i длиннее одного символа, то он одновременно и префикс подстроки длиной i-1. Таким образом, проверяем префикс предыдущей подстроки, если же тот не подходит, то префикс ее префикса, и т.д. Действуя так, находим наибольший искомый префикс.
//описание функции алгоритма Кнута, Морриса и Пратта
int KMPSearch(char *string, char *substring){
int sl, ssl;
int res = -1;
sl = strlen(string);
ssl = strlen(substring);
if ( sl == 0 )
cout << "Неверно задана строка\n";
else if ( ssl == 0 )
cout << "Неверно задана подстрока\n";
else {
int i, j = 0, k = -1;
int *d;
d = new int[1000];
d[0] = -1;
while ( j < ssl - 1 ) {
while ( k >= 0 && substring[j] != substring[k] )
k = d[k];
j++;
k++;
if ( substring[j] == substring[k] )
d[j] = d[k];
else
d[j] = k;
}
i = 0;
j = 0;
while ( j < ssl && i < sl ){
while ( j >= 0 && string[i] != substring[j] )
j = d[j];
i++;
j++;
}
delete [] d;
res = j == ssl ? i - ssl : -1;
}
return res;
}Точный анализ рассматриваемого алгоритма весьма сложен. Д. Кнут, Д. Моррис и В. Пратт доказывают, что для данного алгоритма требуется порядка O(m+n) сравнений символов (где n и m – длины строки и подстроки соответственно), что значительно лучше, чем при прямом поиске.