Потоки в сетях

Теорема (о максимальном потоке и минимальном разрезе). Во всякой сети величина любого максимального потока равна пропускной способности любого минимального разреза.

Первое доказательство. Предположим сначала, что пропускная способность любой дуги является целым числом. В этом случае можно рассматривать сеть как орграф , в котором пропускные способности представляют число дуг, соединяющих различные вершины. Тогда величина максимального потока соответствует в полному числу непересекающихся по дугам простых орцепей из в , а пропускная способность минимального разреза — минимальному числу дуг в 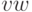— разделяющем множестве. Применяя теперь теорему о целочисленности, мы сразу получим нужный результат.

Чтобы перенести этот результат на сети с рациональными пропускными способностями, умножим все пропускные способности на подходящее целое число (например, наименьшее общее кратное всех знаменателей), чтобы получились целые числа. Тогда приходим к случаю, описанному в предыдущем абзаце, и нужный результат получаем после деления на соответствующей величины максимального потока и пропускной способности минимального разреза.

Наконец, если некоторые из пропускных способностей иррациональны, то теорема доказывается с использованием аппроксимации этих чисел рациональными (с любой заданной точностью) и применением предыдущего результата. При этом аппроксимирующие рациональные числа можно подобрать так, чтобы разность между величиной любого максимального потока и пропускной способностью любого минимального разреза можно было сделать сколь угодно малой. Конечно, на практике иррациональные пропускные способности встречаются крайне редко, поскольку обычно пропускные способности задаются в десятичной форме.

Второе доказательство. Теперь приведем прямое доказательство теоремы о максимальном потоке и минимальном разрезе. Заметим, что поскольку величина любого максимального потока не превышает пропускной способности любого минимального разреза, достаточно доказать существование разреза, пропускная способность которого равна величине данного максимального потока.

Пусть — максимальный поток. Определим два множества и вершин сети: пусть обозначено основание орграфа , соответствующего рассматриваемой сети; тогда вершина сети содержится в в том и только в том случае, если в существует простая цепь , обладающая тем свойством, что любое ее ребро соответствует либо ненасыщенной дуге 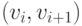, либо дуге , через которую проходит ненулевой поток. (Заметим, что вершина , очевидно, содержится в .) Множество состоит из всех тех вершин, которые не принадлежат .

Покажем теперь, что не пусто и, в частности, содержит вершину . Если это не так, то принадлежит , и тогда в существует простая цепь , обладающая указанным выше свойством. Выберем положительное число , удовлетворяющее следующим двум условиям:

• оно не превышает ни одного из чисел, необходимых для насыщения дуг первого типа;
• оно не превышает потока через любую из дуг второго типа.

Очевидно, что если потоки через дуги первого типа увеличить на , а потоки через дуги второго типа уменьшить на , то величина потока увеличится на . Но это противоречит нашему предположению о том, что — — максимальный поток, и, следовательно, содержится в .

Для завершения доказательства обозначим через множество всех дуг вида 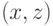, где принадлежит , а принадлежит . Ясно, что является разрезом. Более того, мы видим, что каждая дуга 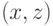из насыщена, так как в противном случае вершина также принадлежала бы . Следовательно, пропускная способность множества должна равняться величине потока , а поэтому и есть искомый разрез.