Графы с цветными ребрами

Реберная раскраска

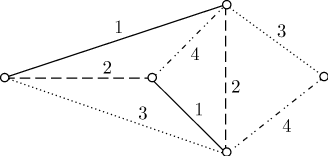
Граф называется реберно - раскрашиваемым, если его ребра можно раскрасить красками таким образом, что никакие два смежных ребра не окажутся одного цвета. Если граф реберно -раскрашиваем, но не является реберно -раскрашиваемым, то называется хроматическим классом или хроматическим индексом, или реберно-хроматическим числом графа . При этом используется запись 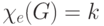. На рисунке изображен граф , для которого .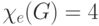

Ясно, что если наибольшая из степеней вершин графа равна , то 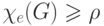. Следующий результат, известный как теорема Визинга, дает точные оценки для хроматического класса графа . Доказательство этой теоремы можно найти у Оре (Ore O. The four-color problem, Academic Press, New York, 1967).

Теорема 7.1.(Визинг, 1964) Пусть в графе , не имеющем петель, наибольшая из степеней вершин равн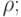а тогда .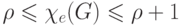

Задача, состоящая в выяснении того, какие графы имеют хроматический класс , а какие 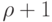, не решена. Однако в некоторых частных случаях соответствующие результаты находятся легко. Например, 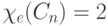или 3 в зависимости от того, четно или нечетно, а , при 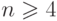. Хроматические классы полных графов и полных двудольных графов вычисляются тоже просто.

Теорема 7.2. .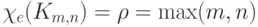

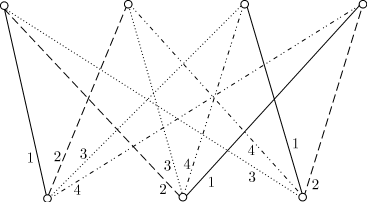
Доказательство

Без потери общности можно считать, что и что граф 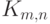изображен так:

вершин расположены на горизонтальной линии под вершинами. Тогда искомая реберная раскраска получается последовательным окрашиванием ребер, инцидентных этим вершинам, с использованием следующих групп красок:

при этом краски из каждой группы располагаются по часовой стрелке, вокруг соответствующей вершины.

Теорема 7.3. 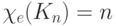, если нечетно , и 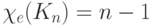, если четно.

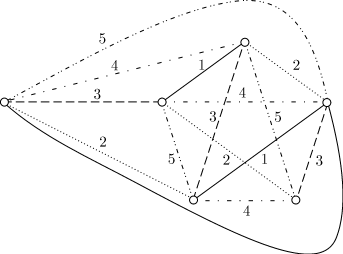
Доказательство

В случае нечетного расположим вершины графа 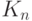в виде правильного -угольника. Тогда его ребра можно раскрасить следующим образом: сначала окрашиваем каждую сторону -угольника в свой цвет, а затем каждое из оставшихся ребер, диагонали -угольника, окрашиваем в тот же цвет, что и параллельная ему сторона.

То, что граф 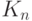не является ребер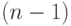но -раскрашиваемым, сразу же следует из того, что максимально возможное число ребер одного цвета равно .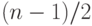

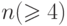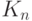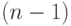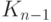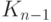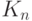В случае четного граф можно рассматривать как соединение полного — графа и отдельной вершины. Если в окрасить ребра описанным выше способом, то для каждой вершины останется один неиспользованный цвет, причем все эти неиспользованные цвета будут различными. Таким образом, чтобы получить реберную раскраску , достаточно окрасить оставшиеся ребра в соответствующие "неиспользованные" цвета.