Паросочетания и свадьбы
Поразительно, что это очевидное необходимое условие является в то же время и достаточным. В этом и состоит теорема Холла о свадьбах ; ввиду ее важности мы приведем три доказательства. Первое из них принадлежит Халмошу и Вогену.
Теорема (Ф. Холл, 1935)
Решение задачи о свадьбах существует тогда и только тогда,
если любые  юношей из данного множества знакомы в совокупности
по меньшей мере с
юношей из данного множества знакомы в совокупности
по меньшей мере с  девушками
девушками 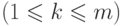 .
.
Доказательство Как было отмечено выше, необходимость условия очевидна. Для
доказательства достаточности воспользуемся индукцией и допустим, что
утверждение справедливо, если число юношей меньше  . (Ясно, что
при
. (Ясно, что
при 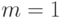 теорема верна.) Предположим теперь, что число юношей
равно
теорема верна.) Предположим теперь, что число юношей
равно  , и рассмотрим два возможных случая.
, и рассмотрим два возможных случая.
(i) Сначала будем считать, что любые  юношей
юношей  ) в совокупности знакомы по меньшей мере с
) в совокупности знакомы по меньшей мере с  девушками (т.e. что
наше условие всегда выполняется "с одной лишней девушкой"). Тогда, если
взять любого юношу и женить его на любой знакомой ему девушке, для
других
девушками (т.e. что
наше условие всегда выполняется "с одной лишней девушкой"). Тогда, если
взять любого юношу и женить его на любой знакомой ему девушке, для
других 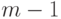 юношей останется верным первоначальное условие. По
предположению индукции
мы можем женить этих
юношей останется верным первоначальное условие. По
предположению индукции
мы можем женить этих 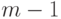 юношей; тем самым доказательство в первом
случае завершено.
юношей; тем самым доказательство в первом
случае завершено.
(ii) Предположим теперь, что имеются  юношей
юношей  , которые в
совокупности знакомы ровно с
, которые в
совокупности знакомы ровно с  девушками. По индуктивному
предположению этих
девушками. По индуктивному
предположению этих  юношей можно женить. Остаются
еще
юношей можно женить. Остаются
еще  юношей,
но любые
юношей,
но любые  из них
из них  должны быть знакомы,
по меньшей
мере, с
должны быть знакомы,
по меньшей
мере, с  девушками из оставшихся, поскольку в противном случае
эти
девушками из оставшихся, поскольку в противном случае
эти  юношей вместе с уже выбранными
юношей вместе с уже выбранными  юношами будут
знакомы меньше, чем
с
юношами будут
знакомы меньше, чем
с  девушками, а это противоречит нашему предположению.
Следовательно, для этих
девушками, а это противоречит нашему предположению.
Следовательно, для этих  юношей выполнено первоначальное
условие, и
по предположению индукции мы можем их женить так, чтобы каждый был
счастлив. Доказательство теоремы закончено.
юношей выполнено первоначальное
условие, и
по предположению индукции мы можем их женить так, чтобы каждый был
счастлив. Доказательство теоремы закончено.
Теорему Холла можно также сформулировать на языке паросочетаний в
двудольном графе; число элементов множества  обозначается
через
обозначается
через 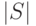 .
.
Следствие Пусть  — двудольный граф, и для любого
подмножества
— двудольный граф, и для любого
подмножества  множества
множества 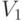 пусть
пусть  —
множество тех вершин из
—
множество тех вершин из 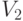 , которые смежны, по крайней мере, с
одной вершиной из
, которые смежны, по крайней мере, с
одной вершиной из  . Тогда совершенное паросочетание
из
. Тогда совершенное паросочетание
из 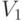 в
в 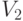 существует в том и только в том случае,
если
существует в том и только в том случае,
если  для каждого
подмножества
для каждого
подмножества  из
из 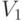 .
.
Доказательство Доказательство этого следствия является просто переводом изложенного выше доказательства на языке теории графов.
