Раскрашивание графов
Гипотеза о четырех красках
Уже сто с лишним лет математики пытаются доказать гипотезу четырех красок. В этом направлении был достигнут значительный прогресс. В печати появилось сообщение (K.Appel, W.Haken, Every planar map is four colorable, Bull. of Amer. Math. Soc., 82, \No\,5 (sept. 1976)), что гипотезу четырех красок удалось обосновать с использованием ЭВМ.
Сформулируем без доказательства несколько относящихся к этой проблеме результатов.
- Если гипотеза четырех красок не верна, то любой опровергающий ее пример
будет очень сложным. Известно, например, что всякий планарный граф,
имеющий менее
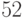 вершин, 4-раскрашиваем.
вершин, 4-раскрашиваем. - Любой не содержащий треугольников планарный граф 3-раскрашиваем (теорема Греча).
- Если попытаться доказать гипотезу четырех красок, то достаточно доказать ее для гамильтоновых планарных графов (довольно неожиданный результат Уитни).
Раскрашивание карт
Возникновение гипотезы четырех красок исторически связано с раскрашиванием географических карт. Если имеется карта с изображением нескольких стран, то интересно узнать, сколько понадобится цветов для такой раскраски этих стран, чтобы никакие две соседние страны не были окрашены в один и тот же цвет. Возможно, самая привычная форма гипотезы четырех красок такова: любую карту можно раскрасить с помощью четырех красок.
Чтобы сделать это утверждение точным, надо определить, что означает слово "карта". Поскольку в рассматриваемых нами задачах о раскраске требуется, чтобы страны, расположенные по обе стороны ребра, были разного цвета, придется исключить карты, обладающие мостом. Таким образом, удобно определить карту как связный плоский граф, не содержащий мостов. Заметим, что при таком определении карты не исключаем петель или кратных ребер.
Назовем карту  - раскрашиваемой, если ее грани можно
раскрасить
- раскрашиваемой, если ее грани можно
раскрасить  красками так, чтобы никакие две смежные грани, то
есть грани, границы которых имеют общее ребро, не были одного цвета. Там, где
можно запутаться, будем использовать термин вершинно
красками так, чтобы никакие две смежные грани, то
есть грани, границы которых имеют общее ребро, не были одного цвета. Там, где
можно запутаться, будем использовать термин вершинно  - раскрашиваемой, имея в виду
- раскрашиваемой, имея в виду  -раскрашиваемость в
описанном выше смысле. Например, изображенный ниже граф является 3-раскрашиваемым
и вершинно 4-раскрашиваемым.
-раскрашиваемость в
описанном выше смысле. Например, изображенный ниже граф является 3-раскрашиваемым
и вершинно 4-раскрашиваемым.
Теперь сформулируем гипотезу четырех красок для карт: всякая карта 4-раскрашиваема.
Теорема 8.3.
Карта  является 2-раскрашиваемой тогда и только
тогда, если
является 2-раскрашиваемой тогда и только
тогда, если  представляет собой эйлеров граф.
представляет собой эйлеров граф.
Доказательство Любую вершину  из
из  должно окружать
четное число граней, так как их можно раскрасить в два цвета. Отсюда следует, что степень каждой
вершины четна, и поэтому
должно окружать
четное число граней, так как их можно раскрасить в два цвета. Отсюда следует, что степень каждой
вершины четна, и поэтому  — эйлеров граф.
— эйлеров граф.
Жордановой кривой, или жордановой дугой, на плоскости называется непрерывная кривая, не имеющая самопересечений; замкнутой жордановой кривой называется жорданова кривая, начало и конец которой совпадают.
Опишем метод, дающий нужную раскраску граней графа  . Выберем
произвольную грань
. Выберем
произвольную грань  и окрасим ее в красный цвет. Проведем
жорданову кривую из точки
и окрасим ее в красный цвет. Проведем
жорданову кривую из точки  грани
грани  в некоторую точку любой
грани, причем так, чтобы эта кривая не проходила ни через какую вершину графа
в некоторую точку любой
грани, причем так, чтобы эта кривая не проходила ни через какую вершину графа  .
Если на пути от точки
.
Если на пути от точки  до точки
до точки  грани
грани 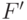 наша кривая пересечет четное
число ребер, окрасим грань
наша кривая пересечет четное
число ребер, окрасим грань 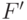 в красный цвет; в противном
случае — в синий.
в красный цвет; в противном
случае — в синий.
Нетрудно показать, что раскрашивание определено корректно: берем
"цикл", состоящий из двух таких жордановых кривых (то есть замкнутую жорданову
кривую), и показываем, что он пересекает четное число ребер графа  (надо использовать индукцию по числу вершин, находящихся внутри цикла, и
тот факт, что каждой вершине графа
(надо использовать индукцию по числу вершин, находящихся внутри цикла, и
тот факт, что каждой вершине графа  инцидентно четное число ребер).
инцидентно четное число ребер).


