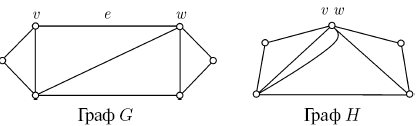
Представления о планарном графе
Гомеоморфные графы
Теорема (Куратовский, 1930)
Граф планарен тогда и только тогда, если не содержит подграфов,
гомеоморфных 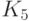 или
или 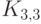 .
.
Поскольку доказательство теоремы Куратовского довольно длинное и сложное,
здесь оно не приводится (см. Ф.Харари. Теория графов. М.: "Мир".
1973). Тем не менее, воспользуемся теоремой Куратовского для получения
другого критерия планарности. Рассмотрим еще два определения. Элементарным стягиванием называется такая процедура: берем
ребро  (вместе с инцидентными ему вершинами, например,
(вместе с инцидентными ему вершинами, например,  и
и  ) и"стягиваем" его, то есть удаляем
) и"стягиваем" его, то есть удаляем  и
отождествляем
и
отождествляем  и
и  .
Полученная при этом вершина инцидентна тем ребрам (отличным от
.
Полученная при этом вершина инцидентна тем ребрам (отличным от  ),
которым первоначально были инцидентны
),
которым первоначально были инцидентны  или
или  .
.
Пример.
Граф  называется стягиваемым к графу
называется стягиваемым к графу  ,
если
,
если  можно получить из
можно получить из  с помощью некоторой
последовательности элементарных стягиваний.
с помощью некоторой
последовательности элементарных стягиваний.
Граф планарен тогда и только тогда, если он не
содержит подграфов, стягиваемых к 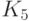 или к
или к 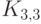 .
.
Формула Эйлера
Для всякого плоского представления связного плоского графа без перегородок
число вершин (  ), число ребер (
), число ребер (  ) и число граней с
учетом
бесконечной (
) и число граней с
учетом
бесконечной (  ) связаны соотношением
) связаны соотношением 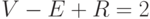 .
.
Пусть граф  — связный, плоский граф без перегородок.
Определим
значение алгебраической суммы
— связный, плоский граф без перегородок.
Определим
значение алгебраической суммы 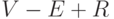 для его произвольного
плоского представления.
для его произвольного
плоского представления.
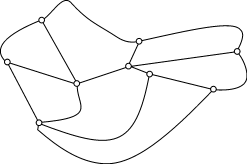
Преобразуем данный граф в дерево, содержащее все его вершины. Для этого
удалим некоторые ребра графа  , разрывая поочередно все его
простые циклы, причем так, чтобы граф оставался связным и без перегородок.
, разрывая поочередно все его
простые циклы, причем так, чтобы граф оставался связным и без перегородок.
Заметим, что при таком удалении одного ребра число граней уменьшается
на  , так как при этом либо пропадет один простой цикл, либо два
простых цикла преобразуются в один. Следовательно, значение разности
, так как при этом либо пропадет один простой цикл, либо два
простых цикла преобразуются в один. Следовательно, значение разности 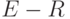 при этом остается неизменным.
при этом остается неизменным.
На рисунке ребра, которые мы удаляем, изображены кривыми. В полученном
дереве обозначим число вершин — 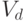 , число ребер —
, число ребер — 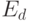 , число граней —
, число граней — 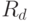 . Справедливо равенство
. Справедливо равенство 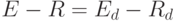 .
.
В дереве одна грань, то есть  . Операция
удаления ребер из графа не меняет число его вершин,
то есть
. Операция
удаления ребер из графа не меняет число его вершин,
то есть 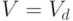 . По теореме 2.1 (см.
"Некоторые определения теории графов"
), в
дереве
. По теореме 2.1 (см.
"Некоторые определения теории графов"
), в
дереве 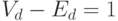 .
Отсюда
.
Отсюда 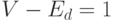 , то есть
, то есть 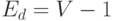 ,
а потому
,
а потому  или
или 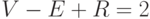 .
.
Итак, доказано, что если в плоском представлении связного графа без
перегородок  вершин,
вершин,  ребер и
ребер и  граней, то
граней, то 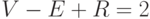 .
Полученная формула называется формулой Эйлера.
.
Полученная формула называется формулой Эйлера.
Пример.