|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Сети очередей
Введение в сети очередей
Сети очередей разделяются на закрытые и открытые сети. В закрытых сетях очередей число клиентов постоянно, тогда как в открытых сетях очередей число клиентов изменяется. В принципе, открытая сеть может быть преобразована в закрытую сеть добавлением дополнительного узла.
Классическая система ожидания Эрланга,  , является примером открытой системы организации очереди, тогда как модель восстановления машин Пальма с
, является примером открытой системы организации очереди, тогда как модель восстановления машин Пальма с  терминалами - закрытая сеть. Если есть более чем один тип клиентов, сеть может быть смешанной закрытой и открытой сетью. Так как процесс выхода из обслуживания от одного узла обычно вызывает процесс поступления вызовов на другой узел, мы обратим особое внимание на процесс выхода из обслуживания, в особенности, когда он может быть отображен как Пуассоновский процесс. Такие системы исследуются в секции, посвященной симметричным системам организации очереди (секция 14.2).
терминалами - закрытая сеть. Если есть более чем один тип клиентов, сеть может быть смешанной закрытой и открытой сетью. Так как процесс выхода из обслуживания от одного узла обычно вызывает процесс поступления вызовов на другой узел, мы обратим особое внимание на процесс выхода из обслуживания, в особенности, когда он может быть отображен как Пуассоновский процесс. Такие системы исследуются в секции, посвященной симметричным системам организации очереди (секция 14.2).
Состояние сети очередей определяется как одновременное распределение числа клиентов на каждом узле. Если  обозначает общее количество узлов, то состояние отображается вектором
обозначает общее количество узлов, то состояние отображается вектором 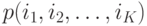 , где
, где  - число клиентов на узле
- число клиентов на узле 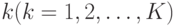 .
.
Часто пространство состояний является очень большим и, решая уравнения равновесия узла, трудно вычислить вероятности состояния. Если каждый узел - симметричная система организации очереди, например, сеть Джексона (секция 14.3), тогда мы будем иметь мультипликативную форму. Вероятности состояния сетей с мультипликативной формой могут быть объединены и получены, используя алгоритм свертывания (секция 14.4.1) с помощью MVA - алгоритма (секция 14.4.2).
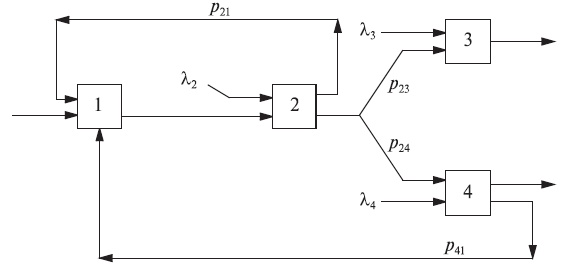
Сети Джексона могут быть обобщены к BCMP-сети (секция 14.5), где есть  типов клиентов. Клиенты одного заданного типа принадлежат так называемой цепочке. Pис.14.1 иллюстрирует пример сети организации очереди с четырьмя цепочками. Когда число цепочек увеличивается, пространство состояний увеличивается соответственно, и точно могут быть вычислены только системы с небольшим количеством цепочек. В случае из многих цепочек сети состояние каждого узла становится многомерным (секция 14.6). Применение мультипликативной формы между узлами, свертывание и MVA -алгоритм рассматриваются в секции 14.7. В литературе можно найти множество алгоритмов для больших сетей, дающих приблизительные результаты.
типов клиентов. Клиенты одного заданного типа принадлежат так называемой цепочке. Pис.14.1 иллюстрирует пример сети организации очереди с четырьмя цепочками. Когда число цепочек увеличивается, пространство состояний увеличивается соответственно, и точно могут быть вычислены только системы с небольшим количеством цепочек. В случае из многих цепочек сети состояние каждого узла становится многомерным (секция 14.6). Применение мультипликативной формы между узлами, свертывание и MVA -алгоритм рассматриваются в секции 14.7. В литературе можно найти множество алгоритмов для больших сетей, дающих приблизительные результаты.
Симметричные системы организации очереди
Чтобы анализировать системы организации очереди, важно знать, является ли процесс выхода из системы организации очереди Пуассоновским процессом.
Четыре модели организации очереди обладают этим свойством.
-
 . По теореме Берка (Burke, 1956 [12]), процесс освобождения
. По теореме Берка (Burke, 1956 [12]), процесс освобождения  -системы - это Пуассоновский процесс. Вероятности пространства состояний были приведены в (12.2):.
-системы - это Пуассоновский процесс. Вероятности пространства состояний были приведены в (12.2):.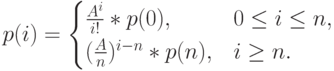
( 14.1) -
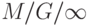 . Эта система соответствует Пуассоновскому процессу (секция 7.2). Из секции 6.3 мы знаем, что случайный переход событий Пуассоновского процесса дает новый Пуассоновский процесс.
. Эта система соответствует Пуассоновскому процессу (секция 7.2). Из секции 6.3 мы знаем, что случайный переход событий Пуассоновского процесса дает новый Пуассоновский процесс.Эта модель иногда обозначается как система с дисциплиной организации очереди с бесконечным числом обслуживающих приборов. Вероятности состояния отображаются Пуассоновским распределением (7.6):
.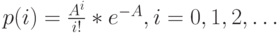
( 14.3) -
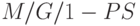 . Это система организации очереди с одним обслуживающим прибором с общим распределением времени обслуживания и совместным использованием процессора. Вероятности состояния такие же, как и для случая
. Это система организации очереди с одним обслуживающим прибором с общим распределением времени обслуживания и совместным использованием процессора. Вероятности состояния такие же, как и для случая 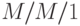 (13.81):.
(13.81):.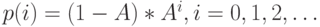
( 14.4) -
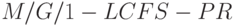 (PR - приоритетное возвращение к работе). Эта система также имеет такие же вероятности состояний, что и
(PR - приоритетное возвращение к работе). Эта система также имеет такие же вероятности состояний, что и 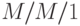 (14.4).
(14.4).
В теории сети очередей обычно рассматривают только эти четыре дис-циплины организации очереди. Хотя, например, для системы с потерями Эрланга процесс освобождения будет также Пуассоновский процесс, если мы рассматриваем и блокированных клиентов. Вышеупомянутые четыре системы организации очереди названы симметричными системами организации очереди, так как они симметричны по времени: процесс поступления вызовов и процесс освобождения - оба Пуассоновские процессы, а системы - обратимы (Kelly, 1979 [60]). Процесс называется обратимым, потому что он дает одну и ту же картину диаграмм состояний, когда мы полностью изменяем ход времени.
Кроме  все эти симметричные системы организации очереди имеют общую особенность: клиент обслуживается немедленно по прибытию. Далее мы главным образом рассматриваем узлы
все эти симметричные системы организации очереди имеют общую особенность: клиент обслуживается немедленно по прибытию. Далее мы главным образом рассматриваем узлы  , Однако модель
, Однако модель 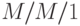 также включает
также включает 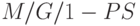 и
и 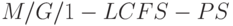 .
.
Теорема Джексона
В 1957 г. Джексон, который работал над планированием производственных систем, издал статью с теоремой, теперь её называют теоремой Джексона (1957). Он показал, что  -узлы сети очередей имеют мультипликативную форму. При использовании основной теоремы Burke (1956 [12]) результат Джексона очевиден. Исторически, первая статья о системах последовательной организации очередей была опубликована Джексоном (1954 [45]).
-узлы сети очередей имеют мультипликативную форму. При использовании основной теоремы Burke (1956 [12]) результат Джексона очевиден. Исторически, первая статья о системах последовательной организации очередей была опубликована Джексоном (1954 [45]).
Теорема 14.1 Джексона. Рассмотрим открытую сеть очередей с  узлами, удовлетворяющую следующим условиям.
узлами, удовлетворяющую следующим условиям.
- Каждый узел соответствует системе организации очереди
 . Узел
. Узел  имеет
имеет 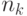 обслуживающих приборов и математическое ожидание времени обслуживания -
обслуживающих приборов и математическое ожидание времени обслуживания - 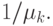
- Клиенты прибывают из внешнего окружения системы на узел
 согласно Пуассоновскому процессу с интенсивностью
согласно Пуассоновскому процессу с интенсивностью 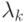 . Заявки от клиентов могут также прибыть от других узлов к узлу
. Заявки от клиентов могут также прибыть от других узлов к узлу  .
. -
Клиент, который только что освободился при обслуживании на узле
 , немедленно переходит на обслуживание узлом
, немедленно переходит на обслуживание узлом  с вероятностью
с вероятностью  или оставляет сеть с вероятностью:
или оставляет сеть с вероятностью:
Клиент может посетить тот же самый узел несколько раз, если
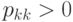 . Средняя интенсивность прибытия
. Средняя интенсивность прибытия 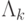 в узле
в узле  получена с использованием уравнений равновесия потока:.
получена с использованием уравнений равновесия потока:.
( 14.5)
Пусть 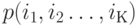 обозначает пространство вероятностей состояний, согласно предположению о статистическом равновесии, то есть вероятности, что есть
обозначает пространство вероятностей состояний, согласно предположению о статистическом равновесии, то есть вероятности, что есть  клиентов на узле
клиентов на узле  . Кроме того, мы принимаем, что:
. Кроме того, мы принимаем, что:
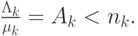 |
( 14.6) |
Тогда пространство вероятностей состояний может быть получено в мультипликативной форме:
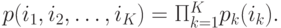 |
( 14.7) |
Для узла  здесь
здесь 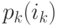 - вероятности состояния системы организации очереди
- вероятности состояния системы организации очереди  с интенсивностью прибытия
с интенсивностью прибытия 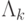 и скоростью обслуживания
и скоростью обслуживания 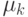 (14.1). Предложенная нагрузка
(14.1). Предложенная нагрузка 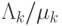 к узлу
к узлу  должна быть меньше, чем емкость
должна быть меньше, чем емкость  узла, чтобы получить статистическое равновесие (14.6).
узла, чтобы получить статистическое равновесие (14.6).
Ключевая точка теоремы Джексона: каждый узел можно рассматривать независимо от всех других узлов и что вероятности состояний можно определить, используя C-формулу Эрланга. Это значительно упрощает вычисление вероятностей пространства состояний. Доказательство теоремы было получено Джексоном в 1957 г., и там показано, что решение удовлетворяет уравнениям равновесия для статистического равновесия.
Первая модель Джексона, таким образом, имеет дело только с открытыми сетями очередей.
Во второй модели Джексона (Джексон, 1963) интенсивность прибытия извне:
 |
( 14.8) |
Может зависеть от текущего числа клиентов в сети. Кроме того, \ik может зависеть от числа клиентов в узле  . Таким способом, мы можем моделировать закрытые, открытые или смешанные сети очередей. Во всех трех случаях вероятности состояния имеют мультипликативную форму.
. Таким способом, мы можем моделировать закрытые, открытые или смешанные сети очередей. Во всех трех случаях вероятности состояния имеют мультипликативную форму.
Модель Gordon & Newell (1967 [31]), которая часто цитируется в литературе, может рассматриваться как специальный случай второй модели Джексона.

Рис. 14.2. Диаграмма переходов состояний открытой сети очередей, состоящей из двух последовательных M/M/1-систем.
Пример 14.3.1 : Два последовательных M/M/1-узла
Pис.14.2 показывает открытую сеть очередей из двух последовательных M/M/1-узлов. Соответствующая диаграмма переходов состояний дается на рис.14.3. Ясно, что диаграмма переходов состояний необратима: между двумя соседними состояниями поток двигается только в одном направлении, (см. секцию 10.2). Очевидно, что мультипликативной формы здесь нет. Однако если мы решаем уравнения равновесия, чтобы получить вероятности состояний, то находим решение, которое может быть написано в мультипликативной форме:
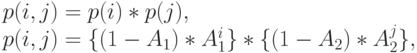
где 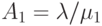 и
и 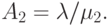 Вероятности состояния могут быть выражены в мультипликативной форме
Вероятности состояния могут быть выражены в мультипликативной форме 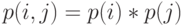 , где
, где 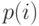 - вероятности состояния для
- вероятности состояния для 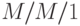 -системы с предложенной нагрузкой
-системы с предложенной нагрузкой  и вероятностью состояния
и вероятностью состояния  для системы
для системы  с предложенной нагрузкой
с предложенной нагрузкой  . Вероятности состояния рис. 14.3 идентичны соответствующим вероятностям на рис.14.4, имеющим местное равновесие и мультипликативную форму.
. Вероятности состояния рис. 14.3 идентичны соответствующим вероятностям на рис.14.4, имеющим местное равновесие и мультипликативную форму.
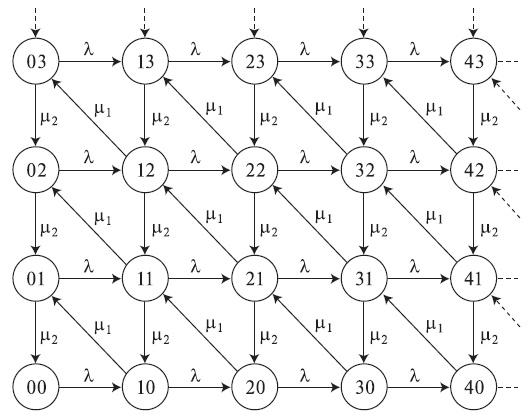
Рис. 14.3. Диаграмма переходов состояний для открытой сети очередей, показанной в рис. 14.2. Диаграмма необратима.
Таким образом, можно найти систему, которая является обратимой и имеет такие же вероятности состояния, что и необратимая система. На рис.14.3. мы имеем региональное, но не местное равновесие. Если рассматривать квадрат из четырех состояний, то по отношению к внешнему миру будет существовать равновесие, но внутренне процесс будет циркулировать с помощью диагонального сдвига состояний.
При обслуживании заявок клиентов на сетях очередей часто будет возникать "зацикливание", когда заявка клиента посещает один и тот же узел несколько раз. Если мы имеем сеть очередей с заявками зацикливания, где узлы - системы  то процессы поступления вызовов к отдельным узлам не будут Пуассоновскими процессами. Так или иначе, мы можем вычислить вероятности состояния, как будто это отдельные независимые узлы
то процессы поступления вызовов к отдельным узлам не будут Пуассоновскими процессами. Так или иначе, мы можем вычислить вероятности состояния, как будто это отдельные независимые узлы  -системы. Это объясняется на следующем примере.
-системы. Это объясняется на следующем примере.
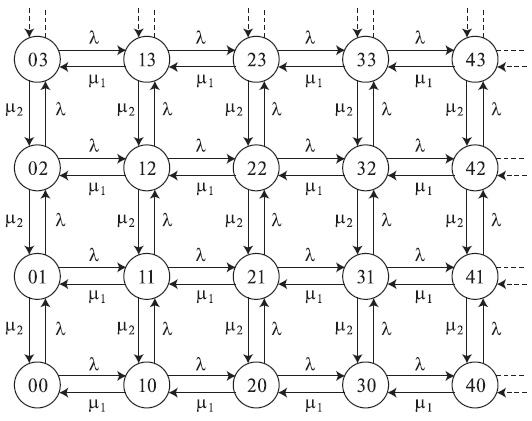
Рис. 14.4. Диаграмма переходов состояний для двух независимых M/M/1-систем организации очереди с идентичной интенсивностью прибытия, но различными средними временами обслуживания. Диаграмма обратима.
Пример 14.3.2: Сети с информацией обратной связи
Прохождение информации с обратной связью приведено в Примере 14.3.1. В этом примере клиенту, который только что закончил свое обслуживание на узле 2, разрешается возвращение к узлу 1 с вероятностью  .
.
С вероятностью клиент покидает систему. Уравнения равновесия потока (14.5) дают полную интенсивность прибытия к каждому узлу, и  должен быть выбран таким, чтобы
должен быть выбран таким, чтобы 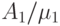 и
и 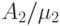 были меньше, чем единица. Предполагая, что
были меньше, чем единица. Предполагая, что 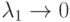 и
и 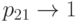 ,, мы понимаем, что реализуемые процессы поступления вызовов не Пуассоновские процессы. Новая заявка от клиента поступает редко, но если поступает и будет введена в систему, то она будет циркулировать относительно долгое время. Число обращений будет геометрически распределено, и интервал поступления - сумма этих двух времен обслуживания. То есть когда в системе есть один (или больше) клиент, интенсивность поступления к каждому узлу будет относительно высока, тогда как если нет никаких клиентов, то интенсивность поступления будет очень низка. Процесс поступления вызовов будет взрывной.
,, мы понимаем, что реализуемые процессы поступления вызовов не Пуассоновские процессы. Новая заявка от клиента поступает редко, но если поступает и будет введена в систему, то она будет циркулировать относительно долгое время. Число обращений будет геометрически распределено, и интервал поступления - сумма этих двух времен обслуживания. То есть когда в системе есть один (или больше) клиент, интенсивность поступления к каждому узлу будет относительно высока, тогда как если нет никаких клиентов, то интенсивность поступления будет очень низка. Процесс поступления вызовов будет взрывной.
Ситуация похожа на разложение экспоненциального распределения во взвешенную сумму Эрланговского распределения k - ого порядка, с геометрическими коэффициентами веса (секция 4.4). Вместо того, чтобы рассматривать единственное экспоненциальное распределение интервала, мы можем анализировать k фаз (рис.4.9) и рассматривать каждую фазу как поступление. Следовательно, процесс поступления вызовов преобразуется из Пуассоновского процесса в процесс с взрывным поступлением.