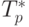Решение систем линейных уравнений
8.2.6. Программная реализация
Рассмотрим возможный вариант параллельной реализации метода Гаусса для решения систем линейных уравнений. Следует отметить, что для получения более простого вида программы для разделения матрицы между процессами используется ленточная последовательная схема (полосы матрицы образуют последовательные наборы соседних строк матрицы). В описании программы реализация отдельных модулей не приводится, если их отсутствие не оказывает влияния на понимание общей схемы параллельных вычислений.
1. Главная функция программы. Реализует логику работы алгоритма, последовательно вызывает необходимые подпрограммы.
// Программа 8.1. — Алгоритм Гаусса решения систем линейных уравнений
int ProcNum; // Число доступных процессоров
int ProcRank; // Ранг текущего процессора
int *pParallelPivotPos; // Номера строк, которые были выбраны ведущими
int *pProcPivotIter; // Номера итераций, на которых строки
// процессора использовались в качестве ведущих
void main(int argc, char* argv[]) {
double* pMatrix; // Матрица линейной системы
double* pVector; // Вектор правых частей линейной системы
double* pResult; // Вектор неизвестных
double *pProcRows; // Строки матрицы A
double *pProcVector; // Блок вектора b
double *pProcResult; // Блок вектора x
int Size; // Размер матрицы и векторов
int RowNum; // Количество строк матрицы
double start, finish, duration;
setvbuf(stdout, 0, _IONBF, 0);
MPI_Init ( &argc, &argv );
MPI_Comm_rank ( MPI_COMM_WORLD, &ProcRank );
MPI_Comm_size ( MPI_COMM_WORLD, &ProcNum );
if (ProcRank == 0)
printf("Параллельный метод Гаусса для решения систем линейных уравнений\n");
// Выделение памяти и инициализация данных
ProcessInitialization(pMatrix, pVector, pResult,
pProcRows, pProcVector, pProcResult, Size, RowNum);
// Распределение исходных данных
DataDistribution(pMatrix, pProcRows, pVector, pProcVector,
Size, RowNum);
// Выполнение параллельного алгоритма Гаусса
ParallelResultCalculation(pProcRows, pProcVector, pProcResult, Size,
RowNum);
// Сбор найденного вектора неизвестных на ведущем процессе
ResultCollection(pProcResult, pResult);
// Завершение процесса вычислений
ProcessTermination(pMatrix, pVector, pResult, pProcRows,
pProcVector, pProcResult);
MPI_Finalize();
}
8.1.
Следует пояснить использование дополнительных массивов. Элементы массива pParallelPivotPos определяют номера строк матрицы, выбираемых в качестве ведущих, по итерациям прямого хода метода Гаусса. Именно в этом порядке должны выполняться затем итерации обратного хода для определения значений неизвестных системы линейных уравнений. Массив pParallelPivotPos является глобальным, и любое его изменение в одном из процессов требует выполнения операции рассылки измененных данных всем остальным процессам программы.
Элементы массива pProcPivotIter определяют номера итераций прямого хода метода Гаусса, на которых строки процесса использовались в качестве ведущих (т.е. строка i процесса выбиралась ведущей на итерации pProcPivotIter[i] ). Начальное значение элементов массива устанавливается нулевым, и, тем самым, нулевое значение элемента массива pProcPivotIter[i] является признаком того, что строка i процесса все еще подлежит обработке. Кроме того, важно отметить, что запоминаемые в элементах массива pProcPivotIter номера итераций дополнительно означают и номера неизвестных, для определения которых будут использованы соответствующие строки уравнения. Массив pProcPivotIter является локальным для каждого процесса.
Функция ProcessInitialization определяет исходные данные решаемой задачи (число неизвестных), выделяет память для хранения данных, осуществляет ввод матрицы коэффициентов системы линейных уравнений и вектора правых частей (или формирует эти данные при помощи какого-либо датчика случайных чисел).
Функция DataDistribution реализует распределение матрицы линейной системы и вектора правых частей между процессорами вычислительной системы.
Функция ResultCollection осуществляет сбор со всех процессов отдельных частей вектора неизвестных.
Функция ProcessTermination выполняет необходимый вывод результатов решения задачи и освобождает всю ранее выделенную память для хранения данных.
Реализация всех перечисленных функций может быть выполнена по аналогии с ранее рассмотренными примерами и предоставляется читателю в качестве самостоятельного упражнения.
2. Функция ParallelResultCalculation. Реализует логику работы параллельного алгоритма Гаусса, последовательно вызывает функции, выполняющие прямой и обратный ход метода.
// Функция для параллельного выполнения метода Гаусса
void ParallelResultCalculation (double* pProcRows,
double* pProcVector, double* pProcResult, int Size, int RowNum) {
ParallelGaussianElimination (pProcRows, pProcVector, Size,
RowNum);
ParallelBackSubstitution (pProcRows, pProcVector, pProcResult,
Size, RowNum);
}3. Функция ParallelGaussianElimination. Функция выполняет параллельный вариант прямого хода алгоритма Гаусса.
// Функция для параллельного выполнения прямого хода метода Гаусса
void ParallelGaussianElimination (double* pProcRows,
double* pProcVector, int Size, int RowNum) {
double MaxValue; // Значение ведущего элемента на процессоре
int PivotPos; // Положение ведущей строки в полосе линейной
// системы даннного процессора
// Структура для выбора ведущего элемента
struct { double MaxValue; int ProcRank; } ProcPivot, Pivot;
// pPivotRow используется для хранения ведущей строки матрицы и
// соответствующего элемента вектора b
double* pPivotRow = new double [Size+1];
// Итерации прямого хода метода Гаусса
for (int i=0; i<Size; i++) {
// Нахождение ведущей строки среди строк процесса
double MaxValue = 0;
for (int j=0; j<RowNum; j++) {
if ((pProcPivotIter[j] == -1) &&
(MaxValue < fabs(pProcRows[j*Size+i]))) {
MaxValue = fabs(pProcRows[j*Size+i]);
PivotPos = j;
}
}
ProcPivot.MaxValue = MaxValue;
ProcPivot.ProcRank = ProcRank;
// Нахождение ведущего процесса (процесса, который содержит
// максимальное значение переменной MaxValue)
MPI_Allreduce(&ProcPivot, &Pivot, 1, MPI_DOUBLE_INT,
MPI_MAXLOC, MPI_COMM_WORLD);
// Рассылка ведущей строки
if ( ProcRank == Pivot.ProcRank ){
pProcPivotIter[PivotPos]= i; // номер итерации
pParallelPivotPos[i]= pProcInd[ProcRank] + PivotPos;
}
MPI_Bcast(&pParallelPivotPos[i], 1, MPI_INT, Pivot.ProcRank,
MPI_COMM_WORLD);
if ( ProcRank == Pivot.ProcRank ){
// заполнение ведущей строки
for (int j=0; j<Size; j++) {
pPivotRow[j] = pProcRows[PivotPos*Size + j];
}
pPivotRow[Size] = pProcVector[PivotPos];
}
MPI_Bcast(pPivotRow, Size+1, MPI_DOUBLE, Pivot.ProcRank,
MPI_COMM_WORLD);
ParallelEliminateColumns(pProcRows, pProcVector, pPivotRow,
Size, RowNum, i);
}
}
8.2.
Функция ParallelEliminateColumns проводит вычитание ведущей строки из строк процесса, которые еще не использовались в качестве ведущих (т.е. для которых элементы массива pProcPivotIter равны нулю).
4. Функция ParallelBackSubstitution. Функция реализует параллельный вариант обратного хода Гаусса.
// Функция для параллельного выполнения обратного хода метода Гаусса
void ParallelBackSubstitution (double* pProcRows, double* pProcVector,
double* pProcResult, int Size, int RowNum) {
int IterProcRank; // Ранг процессора, который содержит ведущую строку
int IterPivotPos; // Положение ведущей строки в полосе процессора
double IterResult; // Вычисленное значение очередной неизвестной
double val;
// Итерации обратного хода метода Гаусса
for (int i=Size-1; i>=0; i--) {
// Вычисление ранга процессора, который содержит ведущую строку
FindBackPivotRow(pParallelPivotPos[i], Size, IterProcRank,
IterPivotPos);
// Вычисление значения неизвестной
if (ProcRank == IterProcRank) {
IterResult = pProcVector[IterPivotPos]/pProcRows[IterPivotPos*Size+i];
pProcResult[IterPivotPos] = IterResult;
}
// Рассылка значения очередной неизвестной
MPI_Bcast(&IterResult, 1, MPI_DOUBLE, IterProcRank, MPI_COMM_WORLD);
// Обновление вектора правых частей
for (int j=0; j<RowNum; j++)
if ( pProcPivotIter[j] < i ) {
val = pProcRows[j*Size + i] * IterResult;
pProcVector[j]=pProcVector[j] - val;
}
}
}
8.3.
Функция FindBackPivotRow определяет строку, из которой можно вычислить значение очередного элемента результирующего вектора. Номер этой строки хранится в массиве pParallelPivotIter. По номеру функция FindBackPivotRow определяет номер процесса, на котором эта строка хранится, и номер этой строки в полосе pProcRows этого процесса.
8.2.7. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта метода Гаусса для решения систем линейных уравнений проводились при условиях, указанных в п. 6.5.5, и состоят в следующем.
Эксперименты производились на вычислительном кластере Нижегородского университета на базе процессоров Intel Xeon 4 EM64T, 3000 МГц и сети Gigabit Ethernet под управлением операционной системы Microsoft Windows Server 2003 Standard x64 Edition и системы управления кластером Microsoft Compute Cluster Server (см. п. 1.2.3).
Для оценки длительности  базовой скалярной операции
проводилось решение системы линейных уравнений при помощи
последовательного алгоритма и полученное таким образом время
вычислений делилось на общее количество выполненных операций – в
результате подобных экспериментов для величины
базовой скалярной операции
проводилось решение системы линейных уравнений при помощи
последовательного алгоритма и полученное таким образом время
вычислений делилось на общее количество выполненных операций – в
результате подобных экспериментов для величины  было получено
значение 4,7 нсек. Эксперименты, выполненные для определения
параметров сети передачи данных, показали значения латентности a
и пропускной способности b соответственно 47 мкс и 53,29 Мбайт/с.
Все вычисления производились над числовыми значениями типа double, т.е. величина w равна 8 байт.
было получено
значение 4,7 нсек. Эксперименты, выполненные для определения
параметров сети передачи данных, показали значения латентности a
и пропускной способности b соответственно 47 мкс и 53,29 Мбайт/с.
Все вычисления производились над числовыми значениями типа double, т.е. величина w равна 8 байт.
Результаты вычислительных экспериментов приведены в таблице 8.1. Эксперименты выполнялись с использованием двух, четырех и восьми процессоров.
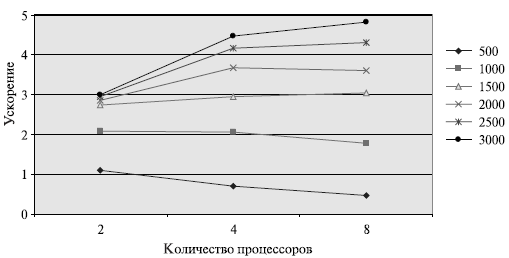
Рис. 8.3. Зависимость ускорения от количества процессоров при выполнении параллельного алгоритма Гаусса для разных размеров систем линейных уравнений
Сравнение времени выполнения эксперимента 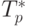 и теоретической
оценки Tp из (8.5) приведено в
таблице 8.2 и на рис. 8.4.
и теоретической
оценки Tp из (8.5) приведено в
таблице 8.2 и на рис. 8.4.