НОУ ИНТУИТ | Теория и практика параллельных вычислений. Лекция 8: Решение систем линейных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.07.2007 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать программу

Аннотация: В лекции рассматривается задача решения систем линейных уравнений. Приводятся необходимые определения и постановка задачи. Описывается последовательный и параллельный варианты одного из прямых методов решения линейных систем общего вида – метода Гаусса. Далее дается описание последовательного и параллельного алгоритмов, реализующих итерационный метод сопряженных градиентов

Ключевые слова: система линейных уравнений, Трансцендентное уравнение, линейное уравнение, решение системы линейных уравнений, алгоритм Гаусса, балансировка вычислений, операции передачи данных, топология сети передачи данных, MPI, вычислительный эксперимент, EM64T, computer cluster, итерационные методы решения систем линейных уравнений, итерационный алгоритм, метод сопряженных градиентов, горизонтальное разделение, программная реализация

Системы линейных уравнений возникают при решении ряда прикладных задач, описываемых дифференциальными, интегральными или системами нелинейных (трансцендентных) уравнений. Они могут появляться также в задачах математического программирования, статистической обработки данных, аппроксимации функций, при дискретизации краевых дифференциальных задач методом конечных разностей или методом конечных элементов и др.

Матрицы коэффициентов систем линейных уравнений могут иметь различные структуру и свойства. Матрицы решаемых систем могут быть плотными, и их порядок может достигать несколько тысяч строк и столбцов. При решении многих задач могут появляться системы, обладающие симметричными положительно определенными ленточными матрицами с порядком в десятки тысяч и шириной ленты в несколько тысяч элементов. И, наконец, при рассмотрении большого ряда задач могут возникать системы линейных уравнений с разреженными матрицами с порядком в миллионы строк и столбцов.

8.1. Постановка задачи

Линейное уравнение с n неизвестными x0, x1, ѕ, xn-1 может быть определено при помощи выражения

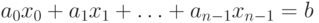$a_0 x_0 + a_1 x_1 + \ldots + a_{n-1} x_{n-1} = b$

( 8.1)

где величины a₀,a₁,...,a_n-1 и b представляют собой постоянные значения.

Множество из n линейных уравнений

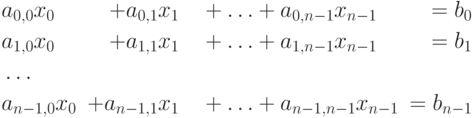$\begin{aligned} & a_{0,0} x_0 & + a_{0,1} x_1 \quad & +\ldots+a_{0,n-1} x_{n-1} & = b_0 \\ & a_{1,0} x_0 & + a_{1,1} x_1 \quad & +\ldots+a_{1,n-1} x_{n-1} & = b_1 \\ & \ldots \\ & a_{n-1,0} x_0 & + a_{n-1,1} x_1 \quad & +\ldots+a_{n-1,n-1} x_{n-1} & = b_{n-1} \end{aligned}$

( 8.2)

называется системой линейных уравнений или линейной системой. В более кратком ( матричном ) виде система может представлена как

Ax = b,

где A=(a_i,j) есть вещественная матрица размера nxn, а векторы b и x состоят из n элементов.

Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.

8.2. Алгоритм Гаусса

Метод Гаусса – широко известный прямой алгоритм решения систем линейных уравнений, для которых матрицы коэффициентов являются плотными. Если система линейных уравнений невырожденна, то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований (не меняющих решение системы (8.2)) к треугольному виду, после чего значения искомых неизвестных могут быть получены непосредственно в явном виде.

В подразделе дается общая характеристика метода Гаусса, достаточная для начального понимания алгоритма и позволяющая рассмотреть возможные способы параллельных вычислений при решении систем линейных уравнений. Более полное изложение алгоритма со строгим обсуждением вопросов точности получаемых решений может быть получено, например, в работах [ [ 6 ] , [ 22 ] , [ 47 ] ] и др.

8.2.1. Последовательный алгоритм

Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решения рассматриваемой системы (такие преобразования носят наименование эквивалентных ). К числу таких преобразований относятся:

умножение любого из уравнений на ненулевую константу;
перестановка уравнений;
прибавление к уравнению любого другого уравнения системы.

Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду

Ux=c,

где матрица коэффициентов получаемой системы имеет вид

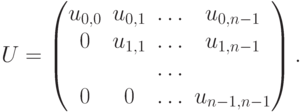
$U= \begin{pmatrix} u_{0,0} & u_{0,1} & \ldots & u_{0, n-1} \\ 0 & u_{1,1} & \ldots & u_{1, n-1} \\ & & \ldots \\ 0 & 0 & \ldots & u_{n-1,n-1} \end{pmatrix} .$

На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д.

8.2.1.1. Прямой ход алгоритма Гаусса

Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i, 0<=i<n-1, метода производится исключение неизвестной i для всех уравнений с номерами k, большими i (т.е. i<k<=n-1 ). Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу ( a_ki/a_ii ), с тем чтобы результирующий коэффициент при неизвестной x_i в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:

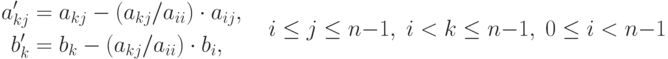
$\left\phantom{(} \begin{aligned} a'_{kj} & = a_{kj}-(a_{kj} / a_{ii})\cdot a_{ij}, \\ b'_k & = b_k-(a_{kj} / a_{ii})\cdot b_i, \end{aligned} \right. \quad i \le j \le n-1, \; i < k \le n-1, \; 0 \le i < n-1$

(следует отметить, что аналогичные вычисления выполняются и над вектором b ).

Поясним выполнение прямого хода метода Гаусса на примере системы линейных уравнений вида:

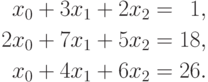
$\begin{aligned} x_0 +3x_1 + 2x_2 = \phantom{0}1, \\ 2x_0 + 7x_1 + 5x_2 = 18, \\ x_0 + 4x_1 + 6x_2 = 26. \end{aligned}$

На первой итерации производится исключение неизвестной x0 из второй и третьей строки. Для этого из этих строк нужно вычесть первую строку, умноженную соответственно на 2 и 1. После этих преобразований система уравнений принимает вид:

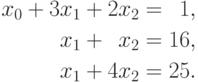
$\begin{aligned} x_0 + 3x_1 + 2x_2=\phantom{0}1, \\ x_1 + \phantom{0}x_2 =16, \\ x_1 + 4x_2 = 25. \end{aligned}$

В результате остается выполнить последнюю итерацию и исключить неизвестную x₁ из третьего уравнения. Для этого необходимо вычесть вторую строку, и в окончательной форме система имеет следующий вид:

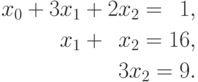
$\begin{aligned} x_0 + 3x_1 + 2x_2=\phantom{0}1, \\ x_1 + \phantom{0}x_2 =16, \\ 3x_2 = 9. \end{aligned}$

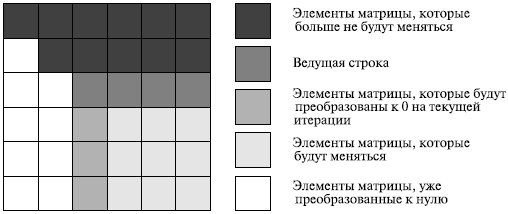
На рис. 8.1 представлена общая схема состояния данных на i -й итерации прямого хода алгоритма Гаусса. Все коэффициенты при неизвестных, расположенные ниже главной диагонали и левее столбца i, уже являются нулевыми. На i -й итерации прямого хода метода Гаусса осуществляется обнуление коэффициентов столбца i, расположенных ниже главной диагонали, путем вычитания строки i, умноженной на нужную ненулевую константу. После проведения (n-1) подобной итерации матрица, определяющая систему линейных уравнений, становится приведенной к верхнему треугольному виду.

Рис. 8.1. Итерация прямого хода алгоритма Гаусса

При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование ведущей, а диагональный элемент ведущей строки называется ведущим элементом. Как можно заметить, выполнение вычислений является возможным только, если ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент a_i,i имеет малое значение, то деление и умножение строк на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма.

Возможный способ избежать подобной проблемы может состоять в следующем: при выполнении каждой очередной итерации прямого хода метода Гаусса следует определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т.е.

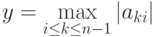
$y=\max_{i\le k\le n-1} |a_{ki}|$

и выбрать в качестве ведущей строку, в которой этот коэффициент располагается (данная схема выбора ведущего значения носит наименование метода главных элементов).

Вычислительная сложность прямого хода алгоритма Гаусса с выбором ведущей строки имеет порядок O(n³).

8.2.1.2. Обратный ход алгоритма Гаусса

После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной x_n-1, после этого из предпоследнего уравнения становится возможным определение переменной x_n-2 и т.д. В общем виде выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:

$\begin{aligned} & x_{x-1} = b_{n-1} / a_{n-1,n-1}, \\ & x_i =(b_i - \sum_{j=i+1}^{n-1} a_{ij}x_j)/a_{ii}, \; i=n-2,n-3,\ldots,0. \end{aligned}$

Поясним, как и ранее, выполнение обратного хода метода Гаусса на примере рассмотренной в п. 8.2.1.1 системы линейных уравнений

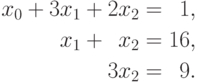
$\begin{aligned} x_0 + 3x_1 + 2x_2=\phantom{0}1, \\ x_1 + \phantom{0}x_2 =16, \\ 3x_2 = \phantom{0}9. \end{aligned}$

Из последнего уравнения системы можно определить, что неизвестная x₂ имеет значение 3. В результате становится возможным разрешение второго уравнения и определение значение неизвестной x₁=13, т.е.

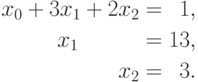
$\begin{aligned} x_0 + 3x_1 + 2x_2=\phantom{0}1, \\ x_1\;\; \phantom{+ 0x_2} =13, \\ x_2 = \phantom{0}3. \end{aligned}$

На последней итерации обратного хода метода Гаусса определяется значение неизвестной x₀, равное -44.

С учетом последующего параллельного выполнения можно отметить, что вычисление получаемых значений неизвестных может выполняться сразу во всех уравнениях системы (и эти действия могут выполняться в уравнениях одновременно и независимо друг от друга). Так, в рассматриваемом примере после определения значения неизвестной x₂ система уравнений может быть приведена к виду

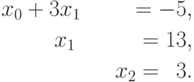
$\begin{aligned} x_0 + 3x_1 \phantom{+ 2x_2}=-5, \\ x_1\;\; \phantom{+ 0x_2} =13, \\ x_2 = \phantom{0}3. \end{aligned}$

Вычислительная сложность обратного хода алгоритма Гаусса составляет O(n²).

Дальше >>

Программирование1500

Теория и практика параллельных вычислений