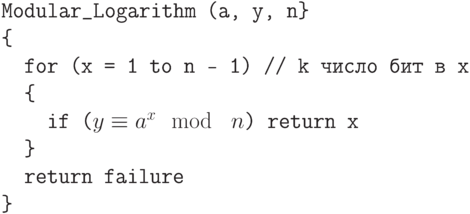|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Квадратичное сравнение
13.2. Возведение в степень и логарифмы
Возведение в степень и логарифм инверсны друг другу. Следующие разделы показывают отношения между ними, в которых a называется основой возведения в степень или логарифма.
Возведение в степень: y = ax -> логарифм: x = logay
Возведение в степень
В криптографии общая модульная операция — возведение в степень. Мы часто должны вычислять
y = ax mod n
Криптографическая система RSA, которая будет обсуждаться влекциях 14-15, использует возведение в степень для шифрования и для дешифрования очень больших чисел. К сожалению, большинство компьютерных языков не имеет операторов, которые могут эффективно вычислять степень, особенно для очень больших чисел. Чтобы сделать эту операцию более эффективной при вычислении, мы нуждаемся в эффективных алгоритмах.
Быстрое возведение в степень
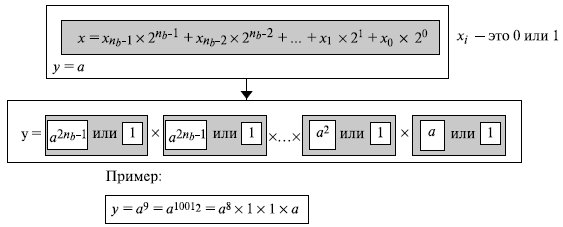
Быстрое возведение в степень возможно при использовании специальных методов возведения в квадрат и умножения. В традиционных алгоритмах, чтобы возводить в степень, применяется только умножение, но быстрый алгоритм возведения в степень использует и возведение в квадрат, и умножение. Главная идея этого метода — выполнение возведения в степень с помощью обработки двоичного числа с nb битами ( 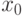 до
до  ). Например, x = 22 = (10110) 2. Вообще, число x может быть записано как
). Например, x = 22 = (10110) 2. Вообще, число x может быть записано как
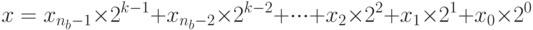
Теперь мы можем написать y = ax, как это показано на рис. 13.3.
Обратите внимание, что y — произведение элементов числа n. Каждый элемент — либо 1 (если соответствующий бит — 0 ), либо a2i (если соответствующий бит — 1 ). Другими словами, элемент a2i участвует в умножении, если бит — 1, или не участвует, если бит — 0 (умножение на 1 не меняет числа). Рисунок 13.3 дает общую идею, как написать алгоритм. Мы можем непрерывно взводить в квадрат 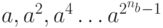 Если соответствующий бит — 0, элемент не участвует в процессе умножения; если бит — 1, то участвует. Алгоритм 13.1 отражает эти два свойства.
Если соответствующий бит — 0, элемент не участвует в процессе умножения; если бит — 1, то участвует. Алгоритм 13.1 отражает эти два свойства.
Возведение_в_ квадрат_и_умножение (a,x,n)
{
y <- 1
for (i <- 0 to nb - 1) //nb — число бит в x
{
if (xi = 1) y <- a x y mod n //умножение, только если бит 1
a <- a2 mod n
} //в последней итерации возведение в степень не нужно
return y
}
13.1.
Алгоритм 13.1
Алгоритм 13.1 использует nb итерации. В каждой итерации он проверяет значение соответствующего бита. Если значение бита равно 1, он умножает текущее значение на предыдущее значение результата. Затем полученный результат является базой для следующей итерации. Обратите внимание, что возведение в квадрат в последнем шаге не нужно (результат не используется).
Пример 13.7
Рисунок 13.4 показывает процесс для подсчета y = ax с использованием алгоритма 13.1 (для простоты изображения модули не показаны). В этом случае x = 22 = (10110) 2. Это число имеет 5 бит.
Возведение в квадрат делается на каждом шаге за исключением последнего. Умножение делается, если соответствующий бит равен 1. На рисунке 13.4 показано, как постепенно формируется значение y до значения y = a22. Затемненный прямоугольник означает, что умножение не делается и предыдущее значение переносится на следующий шаг. Таблица 13.1 показывает, как вычисляется значение для y = 1722 mod 21. Результат — y = 4.
| i | xi | Умножение (Инициализация y = 1) | Возведение в степень (Инициализация a = 17) |
|---|---|---|---|
| 0 | 0 | a = 172 mod 21 =16 | |
| 1 | 1 | y = 1 x 16 mod 21 =16 
|
a = 162 mod 21 = 4 |
| 2 | 1 | y = 16 x 4 mod 21 =1 
|
a = 42 mod 21 =16 |
| 3 | 0 | a = 162 mod 21 = 4 | |
| 4 | 1 | y = 1 x 4 mod 21 = 4 
|
Сложность. Алгоритм 13.1 использует максимально 2nb арифметических операций, в которых nb является длиной модуля в битах (nb = log2n). Сложность в битовых операциях алгоритма — O(nb) или полиномиальная сложность.
Альтернативный алгоритм. Заметим, что алгоритм 13.1 проверяет значение битов в x справа налево (от самого младшего до самого старшего). Может быть написан другой алгоритм, чтобы использовать обратный порядок. Мы выбрали вышеупомянутый алгоритм, потому что операция возведения в квадрат полностью независима от операции умножения; они могут быть сделаны параллельно, чтобы увеличить скорость обработки. Альтернативные алгоритмы оставляем как упражнение.
Логарифм
Мы также должны обсудить модульный логарифм, который используется в криптографии. Если мы применяем возведение в степень для того, чтобы зашифровать или расшифровывать сообщение, противник может использовать логарифм для раскрытия этого сообщения Мы должны знать, трудно ли получить операцию, противоположную возведению в степень.
Полный перебор
Первое решение, которое могло бы прийти на ум, для решения x = loga y (mod n): мы можем написать алгоритм, который непрерывно вычисляет y = ax mod n, пока не находит заданное значение y. Алгоритм 13.2 показывает этот подход.
13.2. Алгоритм 13.2. Алгоритм полного перебора для модульного логарифма
Алгоритм 13.2 явно очень неэффективен. Сложность разрядной операции — 0 (2n) или показательна.
Дискретный логарифм
Второй подход состоит в том, чтобы использовать понятие дискретного логарифма. Рассмотрение этого понятия требует изучения некоторых свойств мультипликативных групп.
Конечная мультипликативная группа. В криптографии мы часто используем мультипликативную конечную группу:  , в которой применяемая операция является умножением. Множество Zn* содержит целые числа от 1 до n–1, которые являются взаимно простыми с n, нейтральный элемент — e = 1. Обратите внимание, что когда модуль группы — простое число, мы имеем
, в которой применяемая операция является умножением. Множество Zn* содержит целые числа от 1 до n–1, которые являются взаимно простыми с n, нейтральный элемент — e = 1. Обратите внимание, что когда модуль группы — простое число, мы имеем 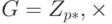 . Эта группа — специальный случай группы первого типа, так что мы концентрируемся на этой группе.
. Эта группа — специальный случай группы первого типа, так что мы концентрируемся на этой группе.
Порядок группы. В лекцииях 5-6 мы обсуждали порядок конечной группы |G| для того, чтобы определить число элементов в группе G. Было доказано, что в группе  порядок группы (число элементов) — число Эйлера
порядок группы (число элементов) — число Эйлера  . Мы показали, как вычислить
. Мы показали, как вычислить  , когда n может быть разложено на множители в виде простых чисел.
, когда n может быть разложено на множители в виде простых чисел.
Пример 13.8
Найти порядок группы 
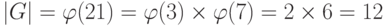 . В этой группе 12 элементов: 1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19 и 20. Все — взаимно простые с 21.
. В этой группе 12 элементов: 1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19 и 20. Все — взаимно простые с 21.
Порядок элемента. В лекциях 5-6 мы также обсуждали порядок элемента — ord (a).
В  мы продолжаем определение. Порядок элемента a есть наименьшее целое число, такое, что
мы продолжаем определение. Порядок элемента a есть наименьшее целое число, такое, что  . В этом случае нейтральный элемент e равен 1.
. В этом случае нейтральный элемент e равен 1.
Пример 13.9
Найдите порядок всех элементов в 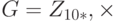 .
.
Решение
Эта группа имеет только  элемента: 1, 3, 7, 9. Мы можем найти порядок каждого элемента методом "проб и ошибок". Однако, согласно результатам лекций 5-6, порядок элемента является делителем порядка группы (теорема Лагранжа). Целые числа, которые делят 4, — 1, 2 и 4. Это означает, что в каждом случае мы должны проверить только эти числа и найти порядок элемента,
элемента: 1, 3, 7, 9. Мы можем найти порядок каждого элемента методом "проб и ошибок". Однако, согласно результатам лекций 5-6, порядок элемента является делителем порядка группы (теорема Лагранжа). Целые числа, которые делят 4, — 1, 2 и 4. Это означает, что в каждом случае мы должны проверить только эти числа и найти порядок элемента,
a. 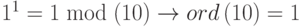 .
.
b.  .
.
c. 
d. 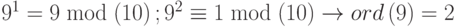 .
.
Теорема Эйлера. Другая теорема, относящаяся к этому вопросу, — это теорема Эйлера, которая говорит, что если a является членом 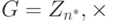 ,
то
,
то  ;
;
Эта теорема очень полезна, потому что показывает, что равенство Ai = 1 mod n сохраняется, если 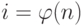 . Заметим: это не отрицает, что равенство может выполняться и если
. Заметим: это не отрицает, что равенство может выполняться и если 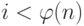 . Другими словами, это отношение показывает, что равенство выполняется по меньшей мере однажды.
. Другими словами, это отношение показывает, что равенство выполняется по меньшей мере однажды.
Пример 13.10
Таблица 13.2 показывает результат ai = x (mod 8) для группы 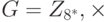 . Обратите внимание, что
. Обратите внимание, что 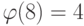 . Это элементы — 1, 3, 5 и 7.
. Это элементы — 1, 3, 5 и 7.
| i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | i=7 | |
| a=1 | x:1 | x:1 | x:1 | x:1 | x:1 | x:1 | x:1 |
|---|---|---|---|---|---|---|---|
| a=3 | x:3 | x:1 | x:3 | x:1 | x:3 | x:1 | x:3 |
| a=5 | x:5 | x:1 | x:5 | x:1 | x:5 | x:1 | x:5 |
| a=7 | x:7 | x:1 | x:7 | x:1 | x:7 | x:1 | x:7 |
Таблица 13.2 показывает некоторые моменты вычислений. Первый: затемненная область показывает результат применения теоремы Эйлера. Когда 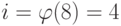 , результат равен x = 1 для каждого a. Второй момент: когда таблица показывает, что значение 1 может быть получено для многих значений i — в первую очередь, значение i, равное порядку элемента (обведено в таблице жирной линией). Порядок элементов: ord (1) = 1, ord (3) = 2, ord (5) = 2 и ord (7) = 2.
, результат равен x = 1 для каждого a. Второй момент: когда таблица показывает, что значение 1 может быть получено для многих значений i — в первую очередь, значение i, равное порядку элемента (обведено в таблице жирной линией). Порядок элементов: ord (1) = 1, ord (3) = 2, ord (5) = 2 и ord (7) = 2.
Первообразные корни. Очень интересное понятие в мультипликативной группе — группы первообразного корня, которые используются в криптографической системе El Gamal (эль Гамаля) в лекциях 14-15. В группе 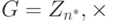 , когда порядок элемента равен
, когда порядок элемента равен  , этот элемент называется первообразным корнем группы.
, этот элемент называется первообразным корнем группы.
Пример 13.11
Таблица 13.2 показывает, что там нет первообразных корней 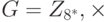 , потому что ни один элемент не имеет порядок, равный
, потому что ни один элемент не имеет порядок, равный 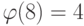 . Порядок всех элементов — меньше, чем 4.
. Порядок всех элементов — меньше, чем 4.
Пример 13.12
Таблица 13.3 показывает результат 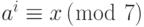 для группы
для группы 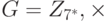 . В этой группе
. В этой группе  .
.
| i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | |
| a=1 | x:1 | x:1 | x:1 | x:1 | x:1 | x:1 |
|---|---|---|---|---|---|---|
| a=2 | x:2 | x:4 | x:1 | x:2 | x:4 | x:1 |
| a=3 | x:3 | x:2 | x:6 | x:4 | x:5 | x:1 |
| a=4 | x:4 | x:2 | x:1 | x:4 | x:2 | x:1 |
| a=5 | x:5 | x:4 | x:6 | x:2 | x:3 | x:1 |
| a=6 | x:6 | x:1 | x:6 | x:1 | x:6 | x:1 |
Порядок элементов – 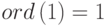 ,
,  ,
,  ,
, 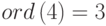 ,
,  и
и  .
Таблица 13.3 показывает, что только два элемента, 3 и 5, имеют порядок в
.
Таблица 13.3 показывает, что только два элемента, 3 и 5, имеют порядок в 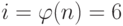 . Поэтому эта группа имеет только два примитивных корня: 3 и 5.
. Поэтому эта группа имеет только два примитивных корня: 3 и 5.
Было доказано, что группа 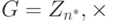 имеет примитивный корень, только если n = 2, 4, pt, или 2pt, в которой p является нечетным простым числом (не 2 ) и t — целое число.
имеет примитивный корень, только если n = 2, 4, pt, или 2pt, в которой p является нечетным простым числом (не 2 ) и t — целое число.