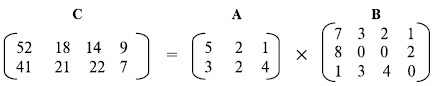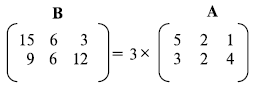|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Сравнения и матрицы
3.1. Матрицы
В криптографии мы должны обрабатывать матрицы. Хотя эта тема принадлежит специальному разделу алгебры, который называется линейной алгеброй, необходим краткий обзор матриц для подготовки к изучению криптографии. Читатели, знакомые с этими вопросами, могут пропустить часть или весь этот раздел. Раздел начинается с некоторых определений и примеров использования матрицы в модульной арифметике.
Определения
Матрица — прямоугольный массив, содержащий l x m элементов, в которых l — число строк, m — число столбцов. Матрица обычно обозначается заглавной буквой, такой, как A. Элемент aij расположен в i -той строке и j -том столбце. Хотя элементы матрицы могут быть любым множеством чисел, мы обсуждаем только матрицы с элементами в Z. Пример матрицы с m столбцами и l строками
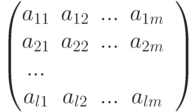
Если матрица имеет только одну строку ( l = 1 ), она называется матрицей-строкой ; если она имеет только один столбец ( m = 1 ), то называется матрицей-столбцом. Матрица называется квадратной, если число строк равно числу столбцов ( l = m ) и содержит элементы a11, a22, ……, amm. Матрица обозначается 0, если все строки и все столбцы содержат нули. Единичная матрица обозначается I, если она квадратная и содержит все единицы на главной диагонали и все нули на других местах. Рисунок 3.2 показывает некоторые примеры матриц с элементами из Z.
Операции и уравнения
В линейной алгебре для матриц определены одно уравнение (равенство) и четыре операции (сложение, вычитание, умножение и скалярное умножение).
Равенство
Две матрицы равны, если они имеют одинаковое число строк и столбцов и соответствующие элементы равны. Другими словами, A = B, если мы имеем aij = bij для всех i и j.
Сложение и вычитание
Операция сложения двух матриц может применяться, если матрицы имеют одинаковое число столбцов и строк. Сложение записывают как C =A + B. В этом случае полученная в результате матрица C имеет тот же самый номер строк и столбцов, как A или B. Каждый элемент C — сумма двух соответствующих элементов A и B: aij + bij.
Операция вычитания производится аналогично сложению, за исключением того, что каждый элемент B вычитается из соответствующего элемента A: dij= aij – bij.
Пример 3.1
Ниже показан пример сложения и вычитания.
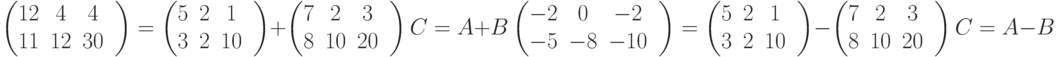
Умножение
Две матрицы различного размера могут быть перемножены, если число столбцов первой матрицы совпадает с числом строк второй матрицы. Если A — матрица размера l x m, а матрица B размера m x p, то произведением будет матрица C размером l x p. Если элемент матрицы A обозначить aij, а каждый элемент матрицы B обозначить bjk, то элемент матрицы C — cik — вычисляется следующим образом:
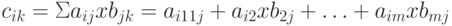
Пример 3.2
Рисунок 3.3 показывает произведение матрицы-строки (  ) на матрицу-столбец (
) на матрицу-столбец (  ). В результате получаем матрицу размером
). В результате получаем матрицу размером  .
.
Пример 3.3
Рисунок 3.4 показывает произведение матрицы  на матрицу
на матрицу  . В результате получаем матрицу
. В результате получаем матрицу 
Скалярное умножение
Мы можем также умножить матрицу на число (называемое скаляр ). Если A — матрица  и x — скаляр, то C = xA — матрица
и x — скаляр, то C = xA — матрица  , в которой
, в которой 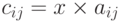 .
.
Пример 3.4
Рисунок 3.5 показывает пример скалярного умножения.