|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Введение в основы современных шифров с симметричным ключом
Блочные шифры как групповые математические перестановки
Как мы увидим в следующих лекциях, нам надо знать, является ли современный блочный шифр математической группой (см. лекции 5-6). Чтобы ответить на этот вопрос, сначала предположим, что ключ достаточно длинный, чтобы создать отображение любой возможной входной информации в выходную. Он называется полноразмерным ключевым шифром. Практически, ключ меньше; длинный ключ можно применять только для некоторых отображений входной информации в выходную. Хотя блочный шифр должен иметь ключ, который является секретным при обмене между передатчиком и приемником, в шифре используются также компоненты, которые не зависят от ключа.
Полноразмерные ключевые шифры
Хотя полноразмерные ключевые шифры практически не используются, мы сначала обсудим их, чтобы сделать более понятным обсуждение шифров с ключом частичного размера.
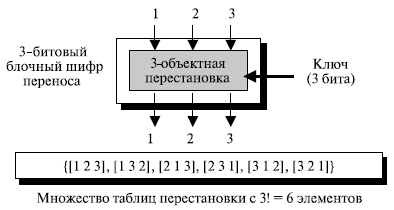
Полноразмерные ключевые блочные шифры транспозиции. Такой ключевой шифр перемещает биты, не изменяя их значения, так что может быть смоделирован как перестановка n -мерного объекта с множеством n! таблиц перестановки, в которых ключ определяет, какая таблица используется Алисой и Бобом. Мы должны иметь n! возможных ключей, и такой ключ должен иметь длину 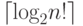 бит.
бит.
Пример 7.3
Покажите модели и множество таблиц перестановки для блочного шифра транспозиции на 3 бита, где размер блока — 3 бита.
Решение
Множество таблиц перестановки имеет 3! = 6 элементов, как показано на рис. 7.2. Ключ должен быть длиной 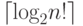 = 3 бита. Заметим, что хотя ключ на 3 бита может выбрать 23 = 8 различных отображений, мы используем только 6 из них.
= 3 бита. Заметим, что хотя ключ на 3 бита может выбрать 23 = 8 различных отображений, мы используем только 6 из них.
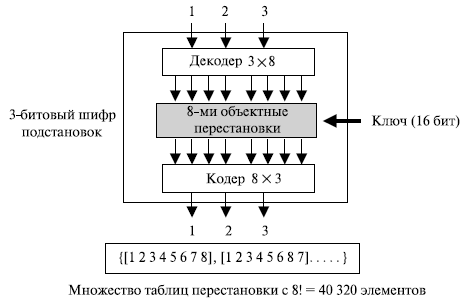
Полноразмерные ключевые блочные шифры подстановки.Такие шифры не перемещают биты — они заменяют биты. На первый взгляд кажется, что полноразмерный ключевой шифр подстановки не может быть смоделирован как перестановка. Однако мы можем применить модель перестановки для шифра подстановки, если сможем декодировать входную информацию и кодировать выходную. Декодирование здесь означает преобразование n -разрядного целого числа в строку 2n -бит с единственной единицей 1 и 2n–1 нулями. Позиция единственной единицы указывает значение целого числа в упорядоченной последовательности позиций строки от 0 до 2n – 1. Поскольку новая входная информация имеет всегда единственную единицу, шифр может быть смоделирован как перестановка 2n! объектов.
Пример 7.4
Покажите модель и множество таблиц перестановки для шифра подстановки блока на 3 бита.
Решение
Три входных исходных текста могут быть обозначены целыми числами от 0 до 7. Это может быть закодировано как строка, содержащая 8 битов с единственной единицей. Например, комбинация 000 может быть закодирована как 00000001 (первая единица справа); комбинация 101 может быть закодирована как 00100000 (шестая единица справа). Рисунок 7.3 показывает модель и множество таблиц перестановки. Заметим, что число элементов в закодированном множестве намного больше, чем число элементов в шифре транспозиции (8! = 40 320). Ключ — также намного более длинный  бит. Хотя ключ на 16 битов может определить 65 536 различных отображений, используются только 40 320.
бит. Хотя ключ на 16 битов может определить 65 536 различных отображений, используются только 40 320.
Групповая перестановка. Факт, что полноразмерная ключевая транспозиция или шифр подстановки/перестановки показывает, что если шифрование (или дешифрование) использует больше чем одну любую комбинацию из этих шифров, результат эквивалентен операции групповой перестановки. Как уже обсуждалось в лекциях 5-6, две или больше каскадных перестановки могут всегда быть заменены единственной перестановкой. Это означает, что бесполезно иметь 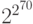 больше чем один каскад полноразмерных ключевых шифров, потому что эффект тот же самый, как и при наличии единственного шага.
больше чем один каскад полноразмерных ключевых шифров, потому что эффект тот же самый, как и при наличии единственного шага.
Шифры ключа частичного размера
Фактические шифры не могут использовать полноразмерные ключи, потому что размер ключа становится несуразно большим, особенно для блочного шифра подстановки. Например, общий шифр подстановки – DES — (см.
"Шифрование, использующее современные шифры с симметричным ключом"
) применяет 64 -разрядный блочный шифр. Если бы проектировщики DES использовали полноразмерный ключ, он был бы 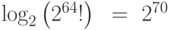 битов. На практике ключ для DES — только 56 битов, что является очень маленьким фрагментом полноразмерного ключа. Это означает, что DES использует только 256 отображений из приблизительно
битов. На практике ключ для DES — только 56 битов, что является очень маленьким фрагментом полноразмерного ключа. Это означает, что DES использует только 256 отображений из приблизительно 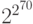 возможных отображений.
возможных отображений.
Группа перестановки. Зададим себе вопрос: можно ли установить, что многоступенчатая транспозиция с частичным ключом или подстановка — это группа перестановки с композицией операций? Ответ на этот вопрос чрезвычайно важен, потому что он говорит нам о том, является ли многоступенчатая версия с частичным шифром таким же средством шифрования, как и сам шифр. Этот факт позволяет достигнуть большей степени безопасности (см. обсуждение многократной DES в "Шифрование, использующее современные шифры с симметричным ключом" ).
Частичный ключевой шифр – это группа, если это — подгруппа соответствующего размера ключа шифра. Другими словами, если полноразмерный ключевой шифр — это группа G = <M, o>, где М. — множество отображений и (o) — композиция операций, то шифр с ключом частичного размера должен представлять подгруппу H = <N, o>, где N — подмножество М с теми же самыми операциями.
Например, было доказано, что многоступенчатый DES с 56 -битовым ключом не является группой, потому что подгруппа с 256 отображениями не может быть создана из группы с 264! отображениями.
Шифры без ключа
Хотя использование отдельно шифра без ключа фактически бесполезно, возможно их применение в качестве компонентов ключевых шифров,
Шифр транспозиции без ключа. Шифры без ключа (или с фиксированным ключом) можно рассматривать как шифр транспозиции, реализованный в аппаратных средствах. Фиксированный ключ (единственное правило перестановки) может быть представлен как таблица в случае реализации шифра в программном обеспечении. Следующая часть этой лекции обсуждает шифры транспозиции без ключа, названные P-блоками, которые используются как стандартные блоки современных блочных шифров.
Шифры подстановки без ключа.Такой шифр без ключа (или с фиксированным ключом) можно представить себе как заранее определенное отображение входной информации к выходной. Отображение может быть представлено как таблица, как математическая функция, а также другими способами. В следующей части этой лекции рассматриваются шифры подстановки без ключей, названные S -блоками, которые применяются как стандартные блоки современных блочных шифров.