|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Алгебраические структуры
Циклические подгруппы
Если подгруппа группы может быть сгенерирована, используя возведение в степень элемента, то такая подгруппа называется циклической подгруппой. Термин возведение в степень здесь означает многократное применение к элементу групповой операции:
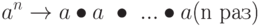
Множество, полученное в результате этого процесса, обозначается в тексте как <a>. Обратите внимание также, что a0 = e.
Пример 5.7
Из группы G = < Z6, +> могут быть получены четыре циклических подгруппы. Это H1 = <{0},+>, H2 =<{0, 2, 4}, +>, H3 = <{0, 3}, +> и H4 = G. Заметим, что когда операция — сложение, то an означает умножение n на a. Заметим также, что во всех этих группах операция — это сложение по модулю 6. Ниже показано, как мы находим элементы этих циклических подгрупп.
a. Циклическая подгруппа, сгенерированная из 0, — это H1, имеет только один элемент (нейтральный элемент).
00 mod 6 = 0 (остановка, далее процесс повторяется).
б. Циклическая подгруппа, сгенерированная на основе 1, — это H4, которая есть сама группа G.
10 mod 6 = 0 11 mod 6 = 1 12 mod 6 = (1 + 1) mod 6 = 2 13 mod 6 = (1 + 1 + 1) mod 6 = 3 14 mod 6 = (1 + 1 + 1 + 1) mod 6 = 4 15 mod 6 = (1 + 1 + 1 + 1 + 1) mod 6 = 5(остановка, далее процесс повторяется)
в. Циклическая подгруппа, сгенерированная на основе 2, — это H2, которая имеет три элемента: 0, 2, и 4.
20 mod 6 = 0 21 mod 6 = 2 22 mod 6 = (2 + 2) mod 6 = 4 (остановка, далее процесс повторяется)
г. Циклическая подгруппа, сгенерированная на основе 3, — это H3, которая имеет два элемента: 0 и 3.
30 mod 6 = 0 31 mod 6 = 3 (остановка, далее процесс повторяется)
д. Циклическая подгруппа, сгенерированная на основе 4, — H2 ; это — не новая подгруппа.
40 mod 6 = 0 41 mod 6 = 4 42 mod 6 = (4 + 4) mod 6 = 2 (остановка, далее процесс повторяется)
е. Циклическая подгруппа, сгенерированная на основе 5, — это H4, она есть сама группа G.
50 mod 6 = 0 51 mod 6 = 5 52 mod 6 = 4 53 mod 6 = 3 54 mod 6 = 2 55 mod 6 = 1 (остановка, далее процесс повторяется)
Пример 5.8
Из группы  можно получить три циклических подгруппы. G имеет только четыре элемента: 1, 3, 7 и 9. Циклические подгруппы —
можно получить три циклических подгруппы. G имеет только четыре элемента: 1, 3, 7 и 9. Циклические подгруппы — 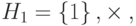
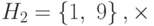 и
и  . Ниже показано, как мы находим элементы этих подгрупп.
. Ниже показано, как мы находим элементы этих подгрупп.
a. Циклическая подгруппа, сгенерированная на основе 1, — это H1. Подгруппа имеет только один элемент, а именно — нейтральный.
10 mod 10 = 1 (остановка, далее процесс повторяется)
б. Циклическая подгруппа, сгенерированная на основе 3, — это H3, которая есть группа G.
30 mod 10 = 1 31 mod 10 = 3 32 mod 10 = 9 33 mod 10 = 7 (остановка, далее процесс повторяется)
в. Циклическая подгруппа, сгенерированная на основе 7, — это H3, которая есть группа G.
70 mod 10 = 1 71 mod 10 = 7 72 mod 10 = 9 73 mod 10 = 3 (остановка, далее процесс повторяется)
г. Циклическая подгруппа, сгенерированная на основе 9, — это H2. Подгруппа имеет только два элемента.
90 mod 10 = 1 91 mod 10 = 9 (остановка, далее процесс повторяется)
Циклические группы
Циклическая группа — группа, которая является собственной циклической подгруппой. В примере 5.7 группа G имеет циклическую подгруппу H5 = G. Это означает, что группа G — циклическая группа. В этом случае элемент, который генерирует циклическую подгруппу, может также генерировать саму группу. Этот элемент далее именуется "генератор". Если g — генератор, элементы в конечной циклической группе могут быть записаны как
{e,g,g2,….., gn-1}, где gn = e.
Заметим, что циклическая группа может иметь много генераторов.
Пример 5.9
а. Группа G = <Z6, +> — циклическая группа с двумя генераторами, g = 1 и g = 5.
б. Группа  — циклическая группа с двумя генераторами, g = 3 и g = 7.
— циклическая группа с двумя генераторами, g = 3 и g = 7.
Теорема Лагранжа
Теорема Лагранжа показывает отношение между порядком группы к порядку ее подгруппы. Предположим, что G — группа и H — подгруппа G. Если порядок G и H — |G| и |H|, соответственно, то согласно этой теореме |H| делит |G|. В примере 5.7 |G| = 6. Порядок подгруппы — |H1| = 1, | H2| = 3, |H3| = 2 и |H4| = 6. Очевидно, все эти порядки есть делители 6.
Теорема Лагранжа имеет очень интересное приложение. Когда дана группа G и ее порядок |G|, могут быть легко определены порядки потенциальных подгрупп, если могут быть найдены делители. Например, порядок группы G = <Z17, +> — это |17|. Делители 17 есть 1 и 17. Это означает, что эта группа может иметь только две подгруппы — нейтральный элемент и H2 = G.
Порядок элемента
Порядок элемента в группе ord (a) (порядок (a)) является наименьшим целым числом n, таким, что a n = e. Иными словами: порядок элемента — порядок группы, которую он генерирует.
Пример 5.10
a. В группе G = <Z6, +>, порядки элементов: порядок ord(0) = 1, порядок ord (1) = 6, порядок ord (2) = 3, порядок ord (3) = 2, порядок ord (4) = 3, порядок ord (5) = 6.
b. В группе G = <Z10, * >, порядки элементов: порядок ord (1) = 1, порядок ord (3) = 4, порядок ord (7) =4, порядок (9) = 2.
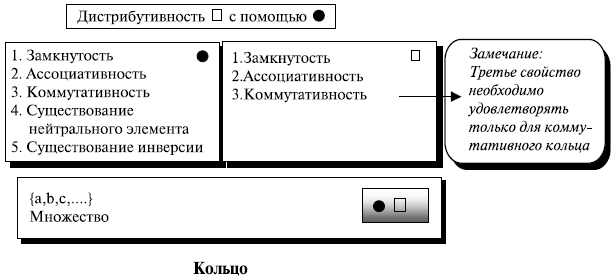
Кольцо
Кольцо, обозначенное как 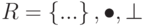 , является алгебраической структурой с двумя операциями. Первая операция должна удовлетворять всем пяти свойствам, требуемым для абелевой группы. Вторая операция должна удовлетворять только первым двум свойствам абелевой группы. Кроме того, вторая операция должна быть распределена с помощью первой. Дистрибутивность означает, что для всех a, b и c элементов из R мы имеем
, является алгебраической структурой с двумя операциями. Первая операция должна удовлетворять всем пяти свойствам, требуемым для абелевой группы. Вторая операция должна удовлетворять только первым двум свойствам абелевой группы. Кроме того, вторая операция должна быть распределена с помощью первой. Дистрибутивность означает, что для всех a, b и c элементов из R мы имеем 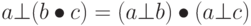 и
и 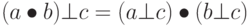 . Коммутативное кольцо — кольцо, в котором коммутативное свойство удовлетворено и для второй операции. Рисунок 5.4 показывает кольцо и коммутативное кольцо.
. Коммутативное кольцо — кольцо, в котором коммутативное свойство удовлетворено и для второй операции. Рисунок 5.4 показывает кольцо и коммутативное кольцо.
Дополнительное замечание
Кольцо включает две операции. Однако вторая операция может не соответствовать третьему и четвертому свойствам. Другими словами, первая операция — фактически операция пары операций, таких как сложение и вычитание; вторая операция может содержать единственную операцию, например умножение, но может не содержать деление.
Пример 5.11
Множество Z с двумя операциями — сложением и умножением — является коммутативным кольцом, которое обозначается 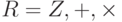 . Сложение удовлетворяет всем пяти свойствам; умножение удовлетворяет только трем свойствам.
. Сложение удовлетворяет всем пяти свойствам; умножение удовлетворяет только трем свойствам.
Умножение дистрибутивно с помощью сложения. Например, 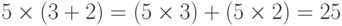 . Хотя, мы можем выполнить на этом множестве сложение и вычитание и умножение, но не деление. Деление не может применяться в этой структуре, потому что оно приводит к элементу из другого множества. Результат деления 12 на 5 есть 2,4, и он не находится в заданном множестве.
. Хотя, мы можем выполнить на этом множестве сложение и вычитание и умножение, но не деление. Деление не может применяться в этой структуре, потому что оно приводит к элементу из другого множества. Результат деления 12 на 5 есть 2,4, и он не находится в заданном множестве.