|
Это в лекции 3. |
Булевы функции и их представления
Булевы функции от n переменных
Булевы функции 1В отечественной литературе их также часто называют функциями алгебры логики. названы в честь английского математика ХIХ века Дж. Буля, который впервые применил алгебраические методы для решения логических задач. Они образуют самый простой нетривиальный класс дискретных функций - их аргументы и значения могут принимать всего два значения (если мощность множества значений функции равна 1, то это тривиальная функция - константа !). С другой стороны, этот класс достаточно богат и его функции имеют много интересных свойств. Булевы функции находят применение в логике, электротехнике, многих разделах информатики.
Обозначим через B двухэлементное множество {0,1}. Тогда
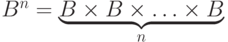
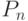 множество всех булевых функций от n переменных. Нетрудно
подсчитать их число.
множество всех булевых функций от n переменных. Нетрудно
подсчитать их число.Теорема 3.1.  .
.
Доказательство.Действительно, по теореме 1.1 число функций из k -элементного множества A в m -элементное множество B равно mk . В нашем случае B={0, 1}, а A = Bn . Тогда m=2 и k= |Bn| = 2n . Отсюда следует утверждение теоремы.
Имеется несколько различных способов представления и интерпретации булевых функций. В этом разделе мы рассмотрим геометрическое и табличное представления, а также представление с помощью логических формул. В "Эквивалентность формул и нормальные формы" будет показано, как булевы функции можно представлять с помощью формул специального вида - дизъюнктивных и конъюнктивных нормальных форм и многочленов Жегалкина. Кроме того, в лекциях "Предварительные сведения" и "Индукция и комбинаторика" (курс "Введение в схемы, автоматы и алгоритмы") будет рассмотрено еще два способа представления булевых функций: логические схемы и упорядоченные бинарные диаграммы решений.
Геометрическое представление
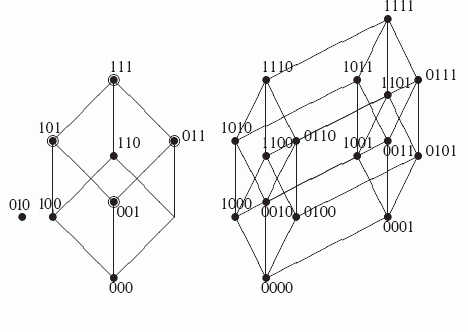
Bn можно рассматривать как единичный n-мерный куб. Каждый набор из нулей и единиц длины n задает вершину этого куба. На рис. 3.1 представлены единичные кубы Bn при n=3,4.
При этом существует естественное взаимно однозначное
соответствие между подмножествами вершин n-мерных единичных кубов
и булевыми функциями от n переменных: подмножеству 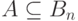 соответствует его характеристическая функция
соответствует его характеристическая функция
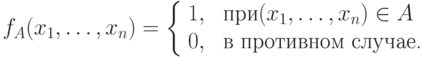
Например, верхней грани куба B3
(ее вершины выделены на рисунке)
соответствует функция f: f(0,0,1)=f(0,1,1)=f(1,0,1)=f(1,1,1) =1 и f(0,0,0)=f(0,1,0)=f(1,0,0)=f(1,1,0) =0.
Очевидно, что указанное соответствие действительно взаимнооднозначное:
каждая булевая функция f от n переменных задает
подмножество Af={(x1, ..., xn)|f(x1, ..., xn)=1}
вершин Bn
. Например, функция, тождественно равная 0,
задает пустое множество 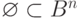 , а функция,
тождественно равная 1, задает множество всех вершин Bn
.
, а функция,
тождественно равная 1, задает множество всех вершин Bn
.
Табличное представление
Булевы функции от небольшого числа аргументов удобно представлять с помощью таблиц. Таблица для функции f(x1, ..., xn) имеет n+1 столбец. В первых n столбцах указываются значения аргументов x1, ..., xn , а в (n+1) -ом столбце значение функции на этих аргументах - f(x1, ..., xn) .
| x1 | . | . | . | xn-1 | xn | f(x1, ..., xn) |
|---|---|---|---|---|---|---|
| 0 | . | . | . | 0 | 0 | f(0, ..., 0,0) |
| 0 | . | . | . | 0 | 1 | f(0, ..., 0,1) |
| 0 | . | . | . | 1 | 0 | f(0, ..., 1,0) |
| . | . | . | . | . | . |  |
| 1 | . | . | . | 1 | 1 | f(1, ..., 1,1) |
Наборы аргументов в строках обычно располагаются в лексикографическом порядке:
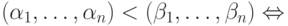 существует такое
существует такое ![i \in [1,n]](/sites/default/files/tex_cache/a66bfd1cad1a41f075cee0957aea46ea.png) , что при
, что при 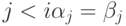 , а
, а 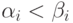 .
.
Если эти наборы рассматривать как записи чисел в двоичной системе счисления,
то 1-ая строка представляет число 0, 2-ая - 1, 3-я - 2, 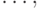 а последняя - 2n-1
.
а последняя - 2n-1
.
При больших n табличное представление становится громоздким, например, для функции от 10 переменных потребуется таблица с 1024 строками. Но для малых n оно достаточно наглядно.