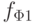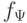|
Это в лекции 3. |
Булевы функции и их представления
Булевы функции и логика высказываний
Как мы уже отметили, Дж. Буль ввел булевы функции для решения логических задач. В логике под высказыванием понимают некоторое повествовательное предложение, относительно которого можно сказать, истинно оно или ложно. Логика высказываний занимается выяснением истинности тех или иных высказываний, связью между истинностью различных высказываний и т.п.
Булевы функции могут служить полезным инструментом при решении многих логических задач.
Каждую переменную можно рассматривать как некоторое элементарное высказывание, принимающее одно из двух значений: 1 (истина) или 0 (ложь). Сложным высказываниям сооответствуют формулы, построенные из элементарных высказываний с помощью логических связок. Вычисляя значения задаваемых ими функций, можно устанавливать зависимости истинностных значений сложных высказываний от значений входящих в них элементарных высказываний. Рассмотрим следующий пример.
Пример 3.1.Пусть известно, что в дорожном проишествии участвовали три автомобиля с водителями A, B и C. Свидетели проишествия дали следующие показания:
- 1-ый свидетель: если A виновен, то из остальных B и C хоть один не виновен;
- 2-ой свидетель: если C не виновен, то виновен кто-то один из пары A, B но не оба вместе;
- 3-ий свидетель: в столкновении виновны не менее двух водителей.
Опишите показания свидетелей в виде булевых формул и постройте таблицу значений их конъюнкции. Можно ли на основании этих показаний сделать вывод, что C является виновником проишествия? Можно ли однозначно определить второго виновника?
Для ответа на эти вопросы введем три переменные, соответствующие следующим
высказываниям: X1
: " виновен A ", X2
: " виновен B " и X3
: " виновен C ". Тогда показания 1-го свидетеля описываются формулой  ,
показания 2-го свидетеля -
,
показания 2-го свидетеля - 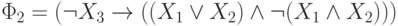 ,
а 3-го свидетеля -
,
а 3-го свидетеля -  .
Показаниям всех трех свидетелей соответствует конъюнкция этих формул
.
Показаниям всех трех свидетелей соответствует конъюнкция этих формул 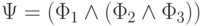 .
Составим таблицы значений для функций
.
Составим таблицы значений для функций  а затем - для
а затем - для 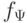 .
.
| X1 | X2 | X3 | (X1 | 
|
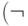
|
X2 | 
|
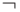
|
X3)) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| X1 | X2 | X3 | 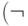
|
X3 | 
|
(( X1 | 
|
X2) | 
|
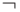
|
(X1 | 
|
X2))) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| \ 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| X1 | X2 | X3 | ((X1 | 
|
X2) | 
|
((X1 | 
|
X3) | 
|
( X2 | 
|
X3))) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| X1 | X2 | X3 | (\Phi1 | 
|
(\Phi2 | 
|
\Phi3)) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
Из этой таблицы следует, что  на двух наборах: (X1=0, X2=1, X3=1)
и (X1=1, X2=0, X3=1)
(строки с этими наборами подчеркнуты).
Поскольку в обоих случаях X3=1
, можно сделать вывод, что С является одним из виновников
проишествия. Однозначно определить второго виновника полученная от свидетелей информация не позволяет,
так как в одном случае им является А, а в другом - В.
на двух наборах: (X1=0, X2=1, X3=1)
и (X1=1, X2=0, X3=1)
(строки с этими наборами подчеркнуты).
Поскольку в обоих случаях X3=1
, можно сделать вывод, что С является одним из виновников
проишествия. Однозначно определить второго виновника полученная от свидетелей информация не позволяет,
так как в одном случае им является А, а в другом - В.
Важную роль в логике играют понятия тождественно истинной и выполнимой формулы.
Булева формула  называется тождественно истинной, если она истинна
при любых значениях входящих в нее переменных, т.е. функция
называется тождественно истинной, если она истинна
при любых значениях входящих в нее переменных, т.е. функция 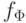 тождественно равна 1.
тождественно равна 1.
Булева формула  называется выполнимой, если существует такой набор
значений переменных, на котором она истинна, т.е. функция
называется выполнимой, если существует такой набор
значений переменных, на котором она истинна, т.е. функция 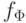 равна 1 хоть на одном наборе аргументов.
равна 1 хоть на одном наборе аргументов.
Как проверить тождественную истинность или выполнимость формулы 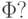 На первый взгляд кажется, что ответ прост - построим по
На первый взгляд кажется, что ответ прост - построим по  таблицу для
функции
таблицу для
функции 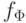 , и, если в столбце значений стоят только единицы, то заключаем, что
, и, если в столбце значений стоят только единицы, то заключаем, что  тождественно истинна, если там есть хоть одна единица, то
тождественно истинна, если там есть хоть одна единица, то  выполнима.
К сожалению, этот способ пригоден только для формул с небольшим числом переменных.
Уже для нескольких десятков и сотен переменных он не годится из-за большого размера
получающейся таблицы - нетрудно подсчитать, что число 290
превосходит количество атомов во всей видимой
вселенной.
выполнима.
К сожалению, этот способ пригоден только для формул с небольшим числом переменных.
Уже для нескольких десятков и сотен переменных он не годится из-за большого размера
получающейся таблицы - нетрудно подсчитать, что число 290
превосходит количество атомов во всей видимой
вселенной.
В математической логике построены аксиоматические системы, позволяющие формализовать человеческие рассуждения о выводимости одних тождественно истинных формул из других (см., например, [15]). В некоторых случаях они позволяют доказать тождественную истинность достаточно длинных формул, имеющих регулярную структуру. Но в общем случае и они практически не применимы для произвольных формул с большим числом переменных.
В теории сложности алгоритмов имеется ряд результатов (они выходят за рамки нашего курса), которые свидетельствуют о том, что эффективных алгоритмов для проверки выполнимости или тождественной истинности произвольной булевой формулы не существует. Вместе с тем для некоторых подклассов формул эти задачи решаются достаточно эффективно. Один такой подкласс - Хорновские формулы - будет рассмотрен далее в "Хорновские формулы и задача получения продукции"