|
Это в лекции 3. |
Предварительные сведения
Множества
Множество - это одно из основных понятий математики, как дискретной, так и непрерывной.
Оно не определяется через другие понятия.
Содержательно, под множеством понимается некоторая совокупность элементов.
Основное отношение между элементами и множеством - это отношение принадлежности элемента множеству.
Оно обозначается знаком 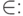
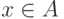 означает, что элемент x принадлежит множеству A.
означает, что элемент x принадлежит множеству A. 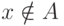 означает, что элемент x не входит в множество A.
означает, что элемент x не входит в множество A. 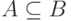 означает, что каждый элемент множества A является также элементом множества B.
В этом случае множество A называется подмножеством множества B.
Если
означает, что каждый элемент множества A является также элементом множества B.
В этом случае множество A называется подмножеством множества B.
Если  и
и 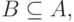 то A=B, т.е. множества A и B равны.
Если
то A=B, т.е. множества A и B равны.
Если  и
и  то A называется собственным подмножеством множества B, и в этом случае пишем
то A называется собственным подмножеством множества B, и в этом случае пишем 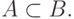 Множество, не содержащее элементов, называется пустым и обозначается
Множество, не содержащее элементов, называется пустым и обозначается  .
.
Обычно множества обозначаются с помощью пары фигурных скобок, в которые заключены их элементы. Небольшие множества задаются прямым перечислением всех элементов. Например, множество простых чисел, не превосходящих 10, это {2, 3, 5, 7} ; множество (имен) летних месяцев: {июнь, июль, август}. В описаниях "больших" конечных множеств используют многоточие. В них часто указывается несколько первых элементов и последний элемент множества. Например, множество целых неотрицательных чисел, не превосходящих 100, записывают как {0, 1, 2, ... , 100}, множество всех месяцев года - как { январь, февраль, ..., декабрь}. Такое задание требует определенной аккуратности. Например, если некоторое множество A задано как {3, 5, 7, ... , 19}, то не ясно, является ли A множеством нечетных чисел, лежащих в интервале от 3 до 19, или это множество простых чисел из того же интервала (возможны и другие его расшифровки). Перечисления элементов бесконечных множеств начинаются несколькими начальными элементами, а завершаются многоточием. При этом часто указывают общий вид элемента задаваемого множества. Основное бесконечное множество, рассматриваемое в дискретной математике, это множество всех натуральных чисел N={1, 2, 3, ... } . Множество всех квадратов этих чисел можно задать, например, так: {1, 4, 9, ..., n2, ... } .
Как мы уже отметили, большие множества не всегда можно точно определить, используя перечисление с многоточием.
Основной способ их описания имеет вид: { Elem | условие на Elem}, где Elem - это общий вид элемента определяемого множества, а после вертикальной черты описано условие, которому этот элемент должен удовлетворять.
Например,  - это множество целых чисел в интервале от 10 до 1000,
- это множество целых чисел в интервале от 10 до 1000,  - множество квадратов натуральных чисел,
- множество квадратов натуральных чисел,  - множество всех простых чисел.
- множество всех простых чисел.
Множества, элементами которых являются другие множества, часто называют семействами или классами.
Семейство ( множество ) всех подмножеств множества A обозначается через 2A, т.е. 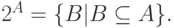 Например, если A={ 0, 1, {2,3}}, то
Например, если A={ 0, 1, {2,3}}, то 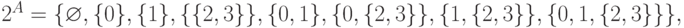 а для пустого множества
а для пустого множества  семейство его подмножеств
семейство его подмножеств 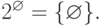
Операции над множествами
Имеется целый ряд операций, позволяющих получать одни множества из других. Рассмотрим основные из них.
Объединением множеств A и B называется множество
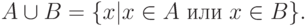
Объединением семейства множеств 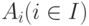 называется множество
называется множество
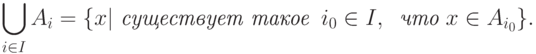
Пересечением множеств A и B называется множество
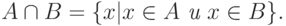
Пересечением семейства множеств 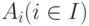 называется множество
называется множество

Из определения операций объединения и пересечения непосредственно следует, что они обладают свойствами ассоциативности: 
 и коммутативности
и коммутативности 
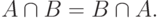
Разностью множеств A и B называется множество

Обычно все рассматриваемые множества являются подмножествами некоторого "универсального" множества U. Разность U \ A называется дополнением множества A (в U ) и обозначается через 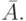 Ясно, что
Ясно, что  и
и 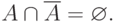
Симметрической разностью множеств A и B называется множество
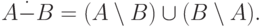
Иногда симметрическую разность множеств называют дизъюнктивной суммой и обозначают  или
или 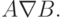
Декартовым (прямым) произведением множеств A1, ... , An называется множество n -ок

Если A1= ... =An=A, то A1 x ... An называется декартовой (прямой) степенью множества A и обозначается через An .
Пример1.1. Пусть заданы множества A= {0,1,... ,n} и B={0,1,... m}, где 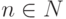 и
и 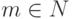 - числа и n < m.
- числа и n < m.
Тогда 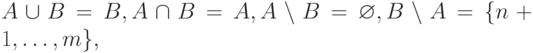 A x B = {(i,j)| 0 <= i <= n, 0 <= j <= m}.
A x B = {(i,j)| 0 <= i <= n, 0 <= j <= m}.
Как доказывать равенство множеств?
Многие математические утверждения, в том числе и многие теоремы в этой книге, имеют следующую форму. Даны разные определения двух множеств A и B. Требуется доказать, что A = B.
Стандартный способ доказательства такого утверждения состоит в доказательстве двух утверждений о включениях:
-
 и
и 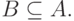
Доказательства этих включений проводятся по такой схеме: рассматривается произвольный элемент, удовлетворяющий определению меньшего множества (слева от знака  ), и устанавливается, что он удовлетворяет также определению большего множества (справа от знака
), и устанавливается, что он удовлетворяет также определению большего множества (справа от знака  ).
).
В качестве примера докажем одно из свойств (законов) дистрибутивности для операций объединения и пересечения:
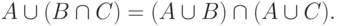
- Пусть a - произвольный элемент из
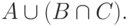 Тогда по определению операции
Тогда по определению операции  имеем
имеем 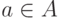 или
или 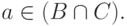 В первом случае из того же определения выводим, что
В первом случае из того же определения выводим, что  и
и 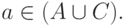 Но тогда по определению операции
Но тогда по определению операции  получаем, что
получаем, что  Во втором случае из определения
Во втором случае из определения  следует, что
следует, что 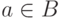 и
и 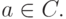 Из этого и из определения
Из этого и из определения  снова следует, что
снова следует, что  и
и 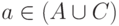 и
и  Таким образом, мы установили, что
Таким образом, мы установили, что 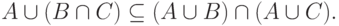
- Пусть теперь
 Тогда по определению операции
Тогда по определению операции  имеем
имеем  и
и 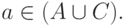 Если
Если 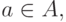 то оба эти включения выполнены.
Но тогда
то оба эти включения выполнены.
Но тогда  Если же
Если же 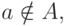 то из первого включения следует, что
то из первого включения следует, что 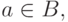 а из второго -
а из второго - 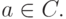 Следовательно,
Следовательно, 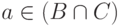 и
и  Таким образом,
Таким образом, 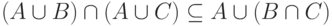 и наше утверждение доказано.
и наше утверждение доказано.
Используя эту же схему, можно установить много других свойств введенных выше операций над множествами и связей между ними (см. задачи 1.2 и 1.5).
