НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

9.6. Задачи для самостоятельного решения

Модель Филда - Нойса "орегонатор"
Простейшая математическая модель периодической химической реакции Белоусова - Жаботинского состоит из трех уравнений:

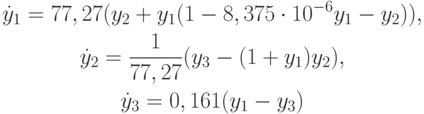
$\begin{gather*} \dot {y}_1 = 77, 27(y_2 + y_1 (1 - 8, 375 \cdot 10^{- 6} y_1 - y_2 )), \\ \dot {y}_2 = \frac{1}{{77, 27}}(y_3 - (1 + y_1 )y_2), \\ \dot {y}_3 = 0, 161(y_1 - y_3 ) \end{gather*}$

На то, что система жесткая, указывают большие различия в константах скоростей реакций — есть процессы быстрые и есть медленные.

Так как переменные системы — концентрации ( HBrO₂, Br^- и Ce(IV) соответственно) то начальные условия для системы следует выбирать положительными, как правило, близкими к 0. Конечное время интегрирования системы T_k = 800.

О системе подробнее, например, в [9.8], [9.9], [9.17].
Уравнение Ван - дер - Поля
Типичным примером жесткой задачи малой размерности является уравнение Ван - дер - Поля [9.8], [9.9], [9.18], [9.19]. Его возможно записать в виде системы

$\begin{gather*} y^{\prime}_1 = y_2, \\ {y^{\prime}_2 = - a(y_2 (y_1^2 - 1) + y_1 ), } \end{gather*}$ ( 9.13)

или в виде

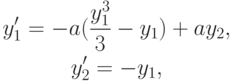
$\begin{gather*} y^{\prime}_1 = - a(\frac{y_1^3}{3} - y_1) + ay_2, \\ y^{\prime}_2 = - y_1, \end{gather*}$ ( 9.14)

(представление Льенара). Считаем, что параметр a — большой. В расчетах рассмотреть два случая: a = 10³ и a = 10⁶. Для тестов обычно полагают y₁ = 2, y₂ = 0.

Конечное время интегрирования системы, записанной в виде (9.13), T_k = 20.

Периодические решения жестких систем ОДУ иногда называют релаксационными автоколебаниями [9.18], [9.19].

Дополнительный вопрос: указать преобразование, переводящее представление (9.13) в представление Льенара (9.14).
Система Ван - дер - Поля и траектории - утки
Рассмотрим неавтономную систему уравнений Ван - дер - Поля:

$\begin{gather*} y^{\prime}_1 = a(- (\frac{y_1^3}{3} - y_1 ) + y_2), \\ y^{\prime}_2 = - y_1 + A\cos \omega t \end{gather*}$

Как и в предыдущей задаче считаем, что a = 10³ и a = 10⁶, y₁ = 2, y₂ = 0. Рассмотреть численно случаи 0 < A < 1 и
$1 < A < \sqrt{1 + \frac{1}{64\omega ^2 }}$
T_k = 200.

О траекториях - утках в системе Ван - дер - Поля см. [9.19] (строгое математическое исследование) и [9.20](популярное изложение).
Суточные колебания концентрации озона в атмосфере
Рассмотрим простейшую математическую модель колебаний концентрации озона в атмосфере [9.2]. Она описывается следующей неавтономной системой ОДУ:

$\begin{gather*} \dot {y_1} = - k_1 y_1 y_2 - k_2 y_1 y_3 + 2k_3 (t)y_2 + k_4 (t)y_3 , \\ \dot {y_2} = 0, \\ \dot {y_1} = k_1 y_1 y_2 - k_2 y_1 y_3 - k_4 (t)y_3 \end{gather*}$

В данной модели уравнения описывают изменение концентрации атомарного кислорода, молекулярного кислорода и озона соответственно. Считается, что изменения концентрации молекулярного кислорода невелики. Начальные значения для задачи таковы:

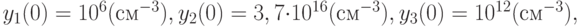
$y_1 (0) = 10^6 (\mbox{см}^{- 3}), y_2 (0) = 3, 7 \cdot 10^{16}(\mbox{см}^{- 3}), y_3 (0) = 10^{12}(\mbox{см}^{- 3}),$
значения констант скоростей химических реакций

$k_1 = 1, 63 \cdot 10^{- 16}, \quad k_2 = 4, 66 \cdot 10^{- 16}.$
Две другие химические реакции зависят от локальной освещенности участка земной поверхности и приближаются следующим выражением:

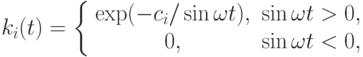
$k_i (t) = \left\{ \begin{array}{cc} \exp (- c_i /\sin \omega t), & \sin \omega t > 0, \\ 0, &\sin \omega t < 0, \\ \end{array} \right.$
где $\omega = \pi /43 200c^{- 1},$ c₃ = 22, 62, c₄ = 7, 601. Значения констант скоростей обращаются в нуль ночью, резко возрастают на рассвете, достигают максимума в полдень и падают до нуля на закате. Конечное время интегрирования T_k = 172800 c (двое суток).

Данная система является жесткой ночью и умеренно жесткой в светлое время суток.
Уравнение Бонгоффера - Ван - дер - Поля
Рассмотрим еще один пример жесткой задачи малой размерности, имеющей периодическое решение [9.19], [9.21].

$\begin{gather*} y^{\prime}_1 = a(- (\frac{y_1^3}{3} - y_1 ) + y_2), \\ y^{\prime}_2 = - y_1 - by_2 + c \end{gather*}$

Здесь a = 10³ и a = 10⁶, y₁ = 2, y₂= 0.

Уравнение описывает протекание тока через клеточную мембрану. Постоянная компонента тока c в безразмерной записи системы такова, что 0 < c < 1, b > 0. T_k = 20.