Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт
Лекция 5:
Численные методы решения экстремальных задач
Аннотация: Рассматриваются наиболее употребительные методы поиска минимума
функций нескольких переменных.
Ключевые слова: метрическое пространство, функция, числовая ось, пространство, функциональное пространство, минимум, функционал, нелинейное программирование, математическое программирование, максимум, целевая функция, связь, системы нелинейных уравнений, значение, производные, стационарная точка, метод перебора, отрезок, погрешность, метод золотого сечения, метод дихотомии, отношение, длина, точность, равенство, метод парабол, исключение, алгоритм, полином, график, коэффициенты, последовательный поиск, метод покоординатного спуска, градиентного спуска, градиент функции, метод сопряженных градиентов, выпуклое множество, хорда, строго выпуклая функция, плоскость, пересечение, линейная функция, задача линейного программирования, вектор
4.1. Поиск безусловного минимума функции
Определение. Пусть на множестве u, состоящем из элементов u линейного метрического пространства определена скалярная функция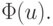 
- Говорят, что
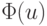имеет локальный минимум на элементе u*, если существует его конечная 
- окрестность, в которой выполнено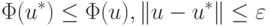
( 4.1) -
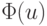достигает глобального минимума в u на элементе u* (строгий, абсолютный минимум), если имеет место равенство
( 4.2)
Замечание. Если u — числовая ось, решается задача на нахождение минимума функции одного переменного, если u — n - мерное векторное пространство, имеется задача на нахождение минимума функции n переменных, если u — функциональное пространство, то решается задача на отыскание функции, доставляющей минимум функционалу (задача оптимального управления или динамического программирования).
Если к (4.1) или (4.2) добавляются условия
( 
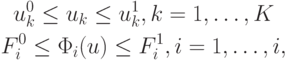
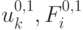— числа, a 
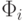— заданные функции), то это задача поиска условного минимума, если подобные ограничения отсутствуют, то это задача поиска безусловного минимума. Причем, если функции 
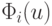линейны, задача поиска условного минимума называется задачей линейного программирования, если хотя бы одна из этих функций нелинейна, то имеется задача нелинейного программирования. Обе эти задачи вместе с задачей динамического программирования в теории оптимального управления называются задачами математического программирования.
Говорится о поиске минимума функции, не ограничивая общности, так как максимум функции 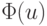является минимумом функции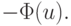 
Отметим связь между задачами вычисления корней системы нелинейных алгебраических уравнений (СНАУ) и задачи минимизации.
Пусть на множестве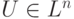 
решается система нелинейных уравнений
f1(u1, ..., un) = 0, ... fn(u1, ..., un) = 0.
Определим целевую функцию следующим образом:
В области U справедливо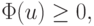 
причем
минимальное значение 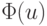имеет при u = u*, где u* — корень рассмотренной системы. Поэтому ее решение эквивалентно поиску минимума 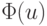в U. Если 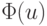строго больше нуля, то система решений не имеет.
Теперь положим, что необходимо найти минимум целевой функции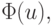 
у которой существуют первые производные. В этом случае задача сводится к решению СНАУ
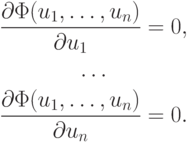
Точка, являющаяся решением указанной СНАУ, называется стационарной. Однако не всякая стационарная точка может быть точкой локального минимума целевой функции.
Следующую теорему приведем без доказательства.
