Интерполяция функций
6.10. Кусочно - многочленная глобальная интерполяция (сплайны)
Определение. Пусть на отрезке [a, b] задана система
узловых точек  Сплайном Sm(t) называется определенная на [a, b] функция, имеющая l непрерывных производных и являющаяся на каждом интервале (tn - 1, tn) многочленом степени m.
Сплайном Sm(t) называется определенная на [a, b] функция, имеющая l непрерывных производных и являющаяся на каждом интервале (tn - 1, tn) многочленом степени m.
Определение. Дефектом сплайна называется разность d = m - l между степенью сплайна и показателем его гладкости l.
Замечание. Для сплайнов также используется обозначение Sm, d(t). Если сплайн строится так, чтобы выполнялись условия Sm(tn) = f(tn), где f(t) — интерполируемая функция, то он называется интерполяционным сплайном. В соответствии с определением, кусочно - линейная функция является интерполяционным сплайном первой степени дефекта 1, кусочно - квадратичная функция с первой непрерывной производной — интерполяционным сплайном второй степени дефекта 1. Наиболее известным в приложениях является интерполяционный кубический сплайн дефекта 1 (естественный сплайн ), который будем обозначать S(t).
Определение. Кубическим сплайном дефекта 1, интерполирующим на отрезке [a, b] заданную функцию f(t), называется функция S(t), удовлетворяющая следующим условиям:
-
S(tn) = f(tn) — условие интерполяции в узлах сетки
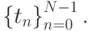
-
![S(t) \in C^2 [a, b],](/sites/default/files/tex_cache/a39f23e43d2ab45e005eeeb2897abac7.png) т.е. является непрерывной вместе с двумя
первыми производными.
т.е. является непрерывной вместе с двумя
первыми производными. - На каждом отрезке [tn, tn + 1], S(t) является кубическим многочленом; n = 0, ..., N - 1.
- На краях отрезка [a, b] заданы краевые условия. Наиболее часто употребляются следующие:
- S'(a) = f'(a), S'(b) = f'(b) ;
- S''(a) = f''(a), S''(b) = f''(b) ; часто полагают S''(a) = S''(b) = 0 ;
- S(a) = S(b), S'(a) = S'(b) ; эти условия называются периодическими, т.е. интерполируемая функция является периодической с периодом b - a.
Покажем, что эта задача имеет единственное решение.
Теорема. Интерполяционный кубический сплайн S(t), удовлетворяющий условиям 1 — 3 и одному из краевых условий 4, существует и единственен.
Доказательство.
Пусть S(z) — эрмитов кубический многочлен, который на каждом отрезке [ tn, tn + 1 ], n = 0, …, N - 1, представлен как
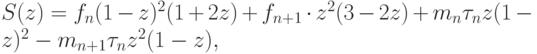
где 
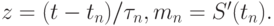 Тогда
Тогда
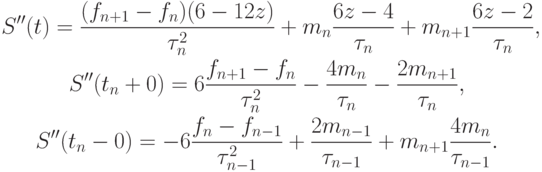
Условие непрерывности второй производной S''(tn + 0) = S''(tn - 0) будет
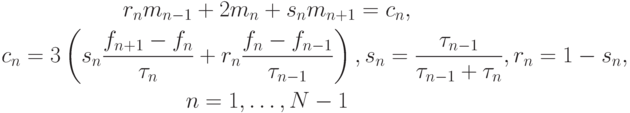
После добавления краевых условий получаем систему из N + 1 уравнение с N + 1 неизвестным mn. Для краевых условий первого типа (заданы первые производные) система выглядит как
m0 = f'0, rn mn - 1 + 2mn + snmn + 1 = cn , mn = f'n
Для условий второго типа (заданы вторые производные)

Аналогично получается СЛАУ для третьего типа краевых условий.
Во всех случаях матрицы СЛАУ оказываются трехдиагональными симметричными, со строгим диагональным преобладанием и, как показывается, положительно определенными, а, следовательно, и неособенными. Следовательно, решение СЛАУ существует и единственно. Отсюда следует существование и единственность решения задачи о построении кубического сплайна.
Приведем еще одно доказательство этой же теоремы.
Доказательство.
Рассмотрим неравномерную сетку: 
 В узлах сетки определены значения функции: fn - 1, fn , fn + 1. Пусть mn — значение второй производной в точке tn (пока неизвестное!). На отрезке [tn, tn + 1] для второй производной кусочно - кубического сплайна имеем
В узлах сетки определены значения функции: fn - 1, fn , fn + 1. Пусть mn — значение второй производной в точке tn (пока неизвестное!). На отрезке [tn, tn + 1] для второй производной кусочно - кубического сплайна имеем
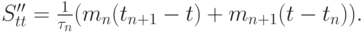 |
( 6.2) |
Так как сплайн — полином третьей степени, то его вторая производная — линейная функция. Интегрируем (6.2) по t, получаем (на отрезке [ tn, tn + 1] )