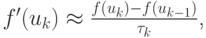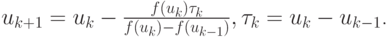НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 6: Численное решение нелинейных алгебраических уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

5.2. Метод Ньютона

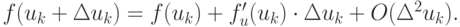
Как и выше, необходимо найти решение уравнения f(u) = 0. Пусть u_k есть k приближение решения ( k итерация ). Следующее приближение ищем в виде $u_{k + 1} = u_{k} + \Delta u_{k},$ разложив функцию f(u) в ряд Тейлора с точностью до членов первого порядка: $f(u_k + \Delta u_k) = f(u_k) + f^{\prime}_u (u_k) \cdot \Delta u_k + O(\Delta ^2 u_k).$

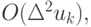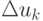Пренебрегая членами $O(\Delta ^{2}u_{k}),$ получим линеаризованное уравнение для определения $\Delta u_{k}$ :

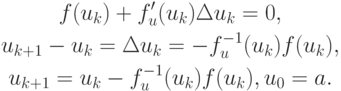
$\begin{gather*} f(u_k) + f_u^{\prime}(u_k)\Delta u_k = 0, \\ u_{{k + 1}} - u_k = \Delta u_k = - f_u^{- 1} (u_k)f(u_k ), \\ u_{{k + 1}} = u_k - f_u^{- 1} (u_k)f(u_k), u_0 = a. \end{gather*}$

Это уже знакомая формула, полученная в результате оптимизации релаксационного варианта метода простой итерации.

Для системы уравнений матрица Якоби ${\mathbf{f^{\prime}}}_{\mathbf{u}} ({\mathbf{u}}_k)$ будет

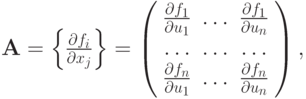
$$ {\mathbf{A}} = \left\{{\frac{\partial f_i}{\partial x_j}}\right\} = \left( \begin{array}{ccc} {\frac{\partial f_1}{\partial u_1}} & \ldots & {\frac{\partial f_1}{\partial u_n}} \\ \ldots & \ldots & \ldots \\ {\frac{\partial f_n}{\partial u_1}} & \ldots & {\frac{\partial f_n}{\partial u_n}} \\ \end{array} \right),$

а метод Ньютона выглядит следующим образом:

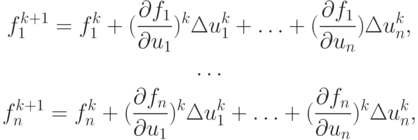
$\begin{gather*} f_1^{k + 1} = f_1^{k} + (\frac{\partial f_1}{\partial u_1})^{k} \Delta u_1^{k} + \ldots + (\frac{\partial f_1}{\partial u_n}) \Delta u_n^{k}, \\ \ldots \\ f_n^{k + 1} = f_n^{k} + (\frac{\partial f_n}{\partial u_1})^{k} \Delta u_1^{k} + \ldots + (\frac{\partial f_n}{\partial u_n})^{k} \Delta u_n^{k}, \end{gather*}$

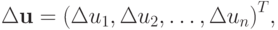
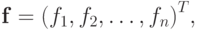
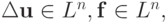
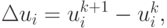где f_i = f_i (u₁, ..., u_n). Приходим к СЛАУ вида ${\mathbf{A}}(\Delta {\mathbf{u}}) = - {\mathbf{f}},$ где $\Delta {\mathbf{u}} = {(\Delta u_1, \Delta u_2, \ldots , \Delta u_n)}^T ,$ ${\mathbf{f}} = {(f_1, f_2, \ldots , f_n)}^T ,$ $\Delta {\mathbf{u}} \in L^{n}, {\mathbf{f}} \in L^{n} ,$ $\Delta u_i = u_i^{k + 1} - u_i^{k} ,$ i = 1, ..., n, k = 0, 1, ....

Рис. 5.2. Геометрическая интерпретация метода Ньютона в одномерном случае

Геометрический смысл метода Ньютона в одномерном случае проиллюстрирован на рис. 5.2. Заменим f(u) в точках u_k — каждом приближении к корню — касательными. За следующее приближение по методу Ньютона примем значение u точки пересечения касательной с осью абсцисс. Метод Ньютона называют также методом линеаризации или методом касательных.

Теорема о квадратичной сходимости метода Ньютона [5.2], [5.4]

Сформулируем и докажем теорему для одномерного (скалярного) случая. Аналогичная теорема будет справедлива и для систем нелинейных уравнений.

Теорема. Пусть существуют первые две ограниченные производные f(u) и, кроме того, существует [f'_u(u)]^{- 1} ; причем имеют место оценки $\left|{f^{\prime\prime}{uu}}\right| \le C_2, \left|{\left[{f^{\prime}(u)}\right]^{- 1}}\right| \le C_1$ (отображение f(u) равномерно невырождено), а начальное приближение выбирается из условия

$C_1^2 C_2 \left| f(u_0)\right| \le q < 1.$

Тогда метод Ньютона сходится с квадратичной скоростью сходимости.

Доказательство.

Разложим f(u_{k + 1}) в ряд Тейлора в окрестности f(u_k), ограничившись квадратичными членами разложения:

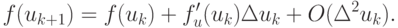
$f(u_{k + 1}) = f(u_{k}) + f'_{u} (u_{k}) \Delta u_{k} + O(\Delta ^{2} u_{k}).$

Здесь введено обозначение 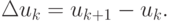$\Delta u_{k} = u_{k + 1} - u_{k}.$ Переходя к абсолютной величине и учитывая, что для метода Ньютона 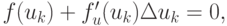$f(u_{k}) + f'_{u}(u_{k}) \Delta u_{k} = 0,$ или $\Delta u = - [f'_{u}(u)]^{ - 1}f(u_{k}),$ получим

$\left|{f(u_{k + 1})}\right| = O(\Delta ^2 u_k) \le C_2 \cdot \Delta ^2 u_k = C_2 \left|{[f^{\prime}_u (u)]^{- 1} f(u_k)}\right|^2 \le C_2 C_1^2 \left|{f(u_k)}\right|^2,$

так как | [f'_u(u)]^{- 1} | < C₁.

Введем в рассмотрение невязку как r_k = | f(u_k) | , получим $r_{k + 1} \le Cr_k^2 ,$ где C = C_2 C_1^2 .

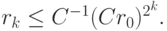
Можно выписать цепочку соотношений $r_1 \le Cr_0^2, r_2 \le Cr_1^2 \le C^3 r_0^4, r_3 \le Cr_2^2 \le C^7 r_0^8 ,$ и т.д., в результате для невязки на k итерации получается выражение $r_k \le C^{- 1} (Cr_0)^{2^k}.$

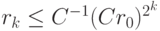Неравенства $r_{k + 1} \le Cr_k^2$ и $r_k \le C^{- 1} (Cr_0)^{2^k}$ являются определением квадратичной скорости сходимости.

Для сходимости итерационного процесса Ньютона достаточно, чтобы было выполнено условие, следующее из последнего неравенства: 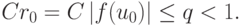$Cr_0 = C \left|f(u_0)\right| \le q < 1.$ Отсюда следуют ограничения на начальное приближение, в частности, $| {f(u_0 )} | \le 1/{C}.$ Теорема доказана.

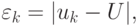Замечание. Несложно показать, что погрешность, определяемая, как $\varepsilon_k = \rho ({\mathbf{u}}_k - {\mathbf{U}}),$ или, в скалярном случае, $\varepsilon _{k} = | u_{k} - U |,$ убывает квадратично. Для этого разложим f(u_{k + 1}) в окрестности u_k в ряд Тейлора до первого члена (или линеаризуем f(u_{k + 1}))

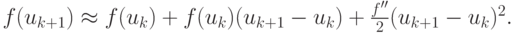
$f(u_{k + 1}) \approx f(u_k) + f(u_k)(u_{{k + 1}} - u_k) + \frac{{f^{\prime\prime}}}{2}(u_{k + 1} - u_k)^2 .$

Так как в методе Ньютона приближения находятся достаточно близко к корню уравнения и $u_{k + 1} \approx U,$ получим

$0 = f(U) = f(u_k) + f^{\prime}(u_k)(U - u_k) + \frac{f^{\prime\prime}}{2}{\left[{(U - u_k)}\right]}^2 .$

Разделив полученное равенство на f'_u(u_k), приходим к оценке

$$ U - \left[{u_k - \frac{f(u_k)}{f^{\prime}(u_k)}}\right] = \frac{{f^{\prime\prime}_u (\theta )}}{{2f^{\prime}_u (u_k)}}(U - u_k)^2 $,$

откуда следует

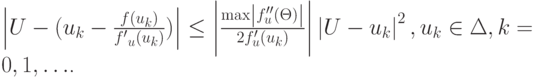
$$ \left| U - (u_k - \frac{f (u_k)}{{f^{\prime}}_u (u_k)})\right| \le \left| \frac{\max \left|f^{\prime\prime}_u(\Theta)\right|}{2f^{\prime}_u(u_k)}\right| \left|U - u_k\right| ^2, u_k \in \Delta , k = 0, 1, \ldots $.$

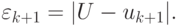Левая часть последнего неравенства по формуле Ньютона равна $\varepsilon _{k + 1} = | U - u_{k + 1} |.$ В таком случае 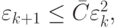$\varepsilon_{{k + 1}} \le \bar {C}\varepsilon _k^2,$ где

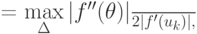
$\bar{C} = \frac{{\max\limits_\Delta } {\left|{f^{\prime\prime}(\theta )}\right|}}{2\left|{f^{\prime}(u_k)}\right|},$

откуда последовательно находим q^(k)[f(u)].

Итерационные процессы, имеющие третий и четвертый порядок сходимости, представляются формулами

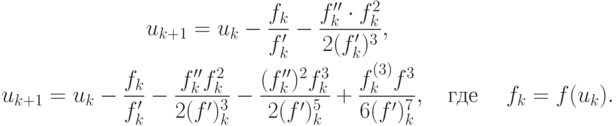
$\begin{gather*} u_{k + 1} = u_k - \frac{f_k}{f_k^{\prime}} - \frac{f_k^{\prime\prime} \cdot f_k^2}{2(f_k^{\prime})^3}, \\ u_{k + 1} = u_k - \frac{f_k}{f_k^{\prime}} - \frac{f_k^{\prime\prime}f^2_k}{2(f^{\prime})^{3}_k} - \frac{(f^{\prime\prime}_k)^{2}f^{3}_k}{2(f^{\prime})^{5}_k} + \frac{f_k^{(3)} f^{3}}{6(f^{\prime})^{7}_k}, \quad \mbox{где }\quad f_k = f(u_k). \end{gather*}$

Отметим, что итерационные методы высших порядков используются достаточно редко вследствие повышенных требований к гладкости функций и необходимости вычисления ее производных и обратных к ним величин.

Иногда для численного решения нелинейных алгебраических систем уравнений, чтобы не вычислять на каждой итерации обратную матрицу, используют упрощенный метод Ньютона

${\mathbf{u}}_{{k + 1}} = {\mathbf{u}}_k - \left[{{\mathbf{f}}_{\mathbf{u}}^{- 1} ({\mathbf{u}}_0)}\right]^{- 1}{\mathbf{f}}({\mathbf{u}}_k), \mathbf{u}_0 = \mathbf{a}.$

Этот метод оказывается приемлемым, поскольку начальное приближение в методе Ньютона обычно выбирается достаточно близким к корню уравнения.

Методом секущих (или разностным методом Ньютона ) называется итерационный метод, в котором вместо производной вычисляется разностное выражение

$$ f^{\prime}(u_k) \approx \frac{{f(u_k) - f(u_{k - 1})}}{{\tau_k}} $,$

откуда

$$ u_{{k + 1}} = u_k - \frac{{f(u_k)\tau_k}}{{f(u_k) - f(u_{k - 1})}}, \tau_k = u_k - u_{k - 1} $.$

Дальше >>

Введение в вычислительную математику

Численное решение нелинейных алгебраических уравнений и систем

5.2. Метод Ньютона

Вопросы и ответы

Студенты

Авторизоваться

Введение в вычислительную математику

Численное решение нелинейных алгебраических уравнений и систем

5.2. Метод Ньютона

Вопросы и ответы

Студенты