НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 4: Численное решение переопределенных СЛАУ. Метод наименьших квадратов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

или

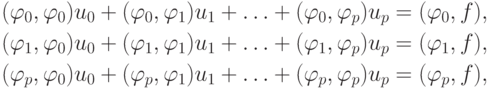
$\begin{gather*} (\varphi_0, \varphi_0) u_0 + (\varphi_0, \varphi_1)u_1 + \ldots + (\varphi_0, \varphi_p)u_p = (\varphi_0, f), \\ (\varphi_1, \varphi_0) u_0 + (\varphi_1, \varphi_1)u_1 + \ldots + (\varphi_1, \varphi_p)u_p = (\varphi_1, f), \\ (\varphi_p, \varphi_0) u_0 + (\varphi_p, \varphi_1)u_1 + \ldots + (\varphi_p, \varphi_p)u_p = (\varphi_p, f), \end{gather*}$

Система метода наименьших квадратов имеет вид 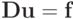$\mathbf{Du} = \mathbf{f}$ с матрицей 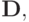$\mathbf{D},$ элементами которой являются скалярные произведения 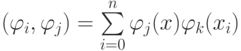$(\varphi_i, \varphi_j) = \sum\limits_{i = 0}^n \varphi_j (x) \varphi_k (x_i)$ Это — матрица Грама. Ее свойства известны из курса линейной алгебры, эта матрица симметричная и положительно определенная. Таким образом, решение исследуемой СЛАУ существует и единственно. В правой части системы стоят проекции свободного члена исходной задачи на подпространство базисных функций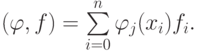 $(\varphi,f) = \sum\limits_{i = 0}^n {\varphi_j(x_i)f_i}.$

Здесь учтено, что

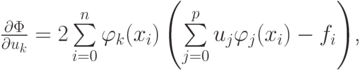
$$ \frac{\partial \Phi }{\partial u_k} = 2 \sum\limits_{i = 0}^n {\varphi_k(x_i)\left({\sum\limits_{j = 0}^p {u_j\varphi_j (x_i) - f_i}} \right)} $,$

или, в развернутом виде

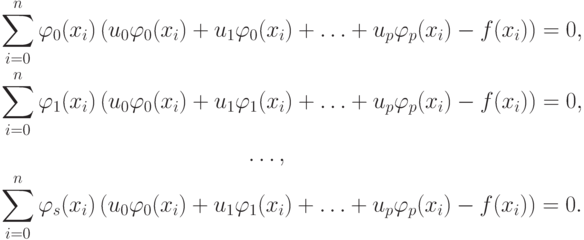
$\begin{gather*} \sum\limits_{i = 0}^n {\varphi_0 (x_i)\left({u_0 \varphi_0 (x_i) + u_1 \varphi_0(x_i) + \ldots + u_p \varphi_p(x_i) - f(x_i)} \right) = 0}, \\ \sum\limits_{i = 0}^n {\varphi_1 (x_i)\left({u_0 \varphi_0 (x_i) + u_1 \varphi_1 (x_i) + \ldots + u_p \varphi_p (x_i) - f(x_i)} \right) = 0}, \\ \ldots, \\ \sum\limits_{i = 0}^n {\varphi_{s} (x_i)\left({u_0 \varphi_0 (x_i) + u_1 \varphi_1 (x_i) + \ldots + u_p \varphi_p (x_i) - f(x_i)} \right) = 0.} \end{gather*}$

Часто выбирают $\varphi_k (x) = x^k,$ в этом случае система уравнений принимает следующую форму:

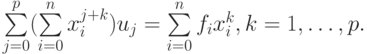
$\sum\limits_{j = 0}^p (\sum\limits_{i = 0}^n x_i^{j + k})u_j = \sum\limits_{i = 0}^n f_i x_i^k, k = 1, \ldots, p.$

Эта система может быть легко выписана в компонентах:

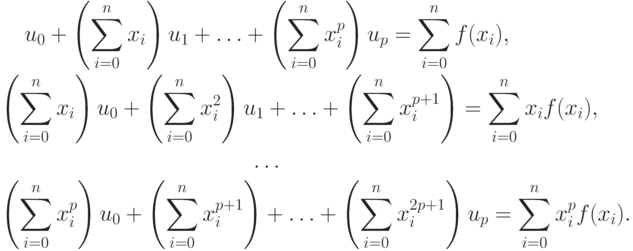
$\begin{gather*} u_0 + \left({\sum\limits_{i = 0}^n {x_i}} \right)u_1 + \ldots + \left({\sum\limits_{i = 0}^n {x_i^p}}\right)u_p = \sum\limits_{i = 0}^n{f(x_i)}, \\ \left({\sum\limits_{i = 0}^n {x_i}} \right)u_0 + \left({\sum\limits_{i = 0}^n {x_i^2}} \right)u_1 + \ldots + \left({\sum\limits_{i = 0}^n {x_i^{p + 1}}} \right) = \sum\limits_{i = 0}^n {x_i f(x_i)}, \\ \ldots \\ \left({\sum\limits_{i = 0}^n {x^p_i}} \right)u_0 + \left({\sum\limits_{i = 0}^n {x^{p + 1}_i}}\right) + \ldots + \left({\sum\limits_{i = 0}^n{x^{2p + 1}_i}}\right)u_p = \sum\limits_{i = 0}^n {x^p_if(x_i)}. \end{gather*}$

В случае использования ортонормированных систем базисных функций 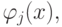$\varphi_j (x),$ т.е., при выполнении условия 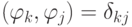$(\varphi_k, \varphi_j) = \delta_{kj}$ решение принимает простой вид

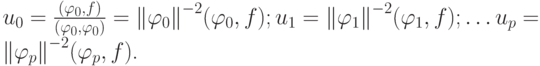
$$ u_0 = \frac{(\varphi_0, f)}{(\varphi_0,\varphi_0)} = {\left\| {\varphi_0} \right\|}^{- 2} (\varphi_0, f); u_1 = {\left\| {\varphi_1} \right\|}^{- 2} (\varphi_1, f); \ldots u_p = {\left\| {\varphi_p} \right\|}^{- 2} (\varphi_p, f) $.$

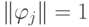Поскольку система функции ортонормирована, то $\left\| {\varphi_j}\right\| = 1$ и $u_k = (\varphi_k, f), k = 1, \ldots, n.$ Эти коэффициенты называются коэффициентами Фурье, а обобщенный многочлен с этими коэффициентами — обобщенным многочленом Фурье. В частности, в качестве базисных можно использовать ортогональную систему функций на $[- \pi, \pi ]: \{\sin{kx},\cos{kx}\}$ k = 1, ..., n. Такие представления называют отрезками тригонометрических рядов Фурье или конечными рядами Фурье .

Докажем теорему о методе наименьших квадратов, обобщающую изложенную информацию.

Запишем переопределенную СЛАУ

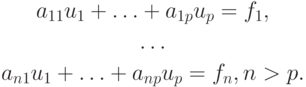$\begin{gather*} a_{11} u_1 + \ldots + a_{1p} u_p = f_1, \\ \ldots \\ a_{n1} u_1 + \ldots + a_{np} u_p = f_n, n > p. \end{gather*}$

( 3.2)

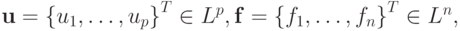
$\mathbf{u} = {\{u_1, \ldots,u_p \}}^T \in L^p, \mathbf{f} = {\{f_1, \ldots,f_n \}}^T \in L^n,$

где линейные нормированные пространства L_p и L_n имеют размерности p и n соответственно. Перепишем (3.2) в матричной форме:

$\mathbf{Au} = \mathbf{f},$

где

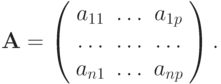
$\mathbf{A} = \left( \begin{array}{ccc} {a_{11}} & \ldots & {a_{1p}} \\ \ldots & \ldots & \ldots \\ {a_{n1}} & \ldots & {a_{np}}} \end{array} \right).$

Наряду с основным скалярным умножением в L_n

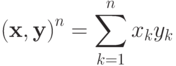${(\mathbf{x},\mathbf{y})}^n = \sum\limits_{k = 1}^n{x_k y_k}$

( 3.3)

введем скалярное умножение с весовой матрицей 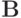$\mathbf{B}$ :

${\left[{\mathbf{x},\mathbf{y}}\right]}^n = {(\mathbf{Bx},\mathbf{y})}^n, \mathbf{B} = {\mathbf{B}}^* > 0, \mathbf{x}, \mathbf{y} \in L^n$

( 3.4)

Оба этих умножения удовлетворяют аксиомам скалярного умножения элементов линейного пространства. Матрица 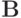$\mathbf{B}$ является весовой и определяет вклад невязки каждого слагаемого суммы (3.1). Система (3.2) не имеет классического решения. Определим обобщенное решение этой системы как элемент линейного пространства 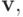$\mathbf{v},$ придающий наименьшее значение квадратичной форме:

$\Phi (\mathbf{u}) = {\left[\mathbf{Au} - \mathbf{f}, \mathbf{Au} - \mathbf{f}\right]}^n.$

Дальше >>

Введение в вычислительную математику

Численное решение переопределенных СЛАУ. Метод наименьших квадратов

Вопросы и ответы

Студенты

Авторизоваться

Введение в вычислительную математику

Численное решение переопределенных СЛАУ. Метод наименьших квадратов

Вопросы и ответы

Студенты