Три алгоритма на графах

Поиск в глубину и задача о лабиринте

Задача поиска выхода из лабиринта известна с древних времен. В терминах графов ее можно формализовать так: лабиринт - это неориентированный граф, вершины которого представляют "перекрестки" лабиринта, а ребра - дорожки между соседними перекрестками. Одна или несколько вершин отмечены как выходы. Задача состоит в построении пути из некоторой исходной вершины в вершину-выход.

В этом разделе мы рассмотрим метод обхода всех вершин графа, называемый поиском в глубину. Его идею кратко можно описать так:

находясь в некоторой вершине v, идем из нее в произвольную еще не посещенную смежную вершину w, если такой вершины нет, то возвращаемся в вершину, из которой мы пришли в v.

Алгоритм поиска в глубину

Вход: G=(V, E) - неориентированный граф, представленный списками смежностей: для каждой 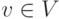список L_v содержит перечень всех смежных с v вершин.

Выход: NUM[v] - массив с номерами вершин в порядке их прохождения и множество (древесных) ребер 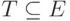, по которым осуществляется обход.

Алгоритм ПОГ

1. T = {}; NOMER = 1;
2. для каждой вершины 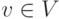положим NUM[v] = 0 и пометим v как "новую";
3. ПОКА существует "новая" вершина
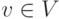
4. ВЫПОЛНЯТЬ ПОИСК(v).

Основную роль в этом алгоритме играет следующая рекурсивная процедура.

Алгоритм ПОИСК(v):

1.   пометить v как "старую";
2.   NUM[v] = NOMER;  NOMER = NOMER + 1;
3.   ДЛЯ КАЖДОЙ   w принадлежащей Lv   ВЫПОЛНЯТЬ
4.         ЕСЛИ   вершина   w   "новая"
5.            ТО
6.            { добавить (v, w)   к   T;
7.               ПОИСК(w);
8.            }

Теорема 11.2. Алгоритм ПОГ обходит (нумерует) все вершины графа G=(V,E). Если G - связный граф, то S=(V,T) - это остов G, если граф G не является связным, то S=(V,T) - это остовной лес для G, т.е. объединение остовных деревьев для каждой из компонент связности G.

Доказательство Первое утверждение следует из того, что по окончании алгоритма ПОГ все вершины графа старые, а это значит, что для каждой из них вызывалась процедура ПОИСК, которая в стр.2 присвоила номер.

Заметим теперь, что если ребро (v, w) попадает в T, то вызов процедуры ПОИСК(w) происходит после вызова ПОИСК(v) и поэтому NUM[v] < NUM[w]. Существование цикла в S означало бы, что для некоторого ребра из T это свойство нарушено (почему?). Следовательно, в S циклов нет.

Пусть G₁=(V₁,E₁) - связная компонента G и 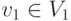- первая ее вершина, для которой вызывается процедура ПОИСК. Тогда для каждой вершины внутри вызова ПОИСК(v₁) произойдет вызов ПОИСК(w).

Это утверждение доказывается индукцией по расстоянию ( длине кратчайшего пути ) от v₁ до w.

Если это расстояние равно 1, то и рассматривается в вызове ПОИСК(v₁) в стр.3. Если w в этот момент "старая", то, значит, ПОИСК(w) уже вызывался. Если же w "новая", то в стр. 7 происходит вызов ПОИСК(w).

Предположим теперь, что ПОИСК(u) вызывается для всех вершин u, находящихся на расстоянии k >= 1 от v₁, и пусть вершина 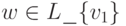находится на рсстоянии (k + 1) от v₁. Тогда имеется путь длины (k + 1) от v₁ до w . Пусть u - это предпоследняя вершина на этом пути. Тогда расстояние от v₁ до u равно k и по нашему предпроложению в некоторый момент выполняется вызов ПОИСК(u). Так как 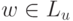, то в этом вызове вершина w в некоторый момент рассматривается в цикле в стр.3. Как и выше, если она в этот момент "старая", то ПОИСК(w) уже вызывался. Если же w еще "новая", то в стр.7 происходит вызов ПОИСК(w).

Также по индукции замечаем, что если вызов ПОИСК(w) произошел внутри вызова ПОИСК(v), то в T имеется путь из v в w. Следовательно, граф S₁=(V₁,T₁), построенный в процессе вызова ПОИСК(v) является деревом с корнем v.

Дерево S=(V,T), которое строится алгоритмом ПОГ, называется глубинным остовом или глубинным остовным деревом графа G. Ребра, попавшие в множество T, называются прямыми, а не попавшие в это множество ребра из множества (E \ T) - обратными. Каждое обратное ребро (v,w) соединяет вершину v с ее предком w в глубинном остове (см. задачу 11.8). Поэтому в исходном графе G оно определяет цикл: от w к v по ребрам дерева T, а затем обратно от v к w по ребру (v,w). Поэтому алгоритм ПОГ можно использовать для проверки наличия циклов в G. Ребро (v,w) не добавляется к T, т.е. является обратным, тогда и только тогда, когда в стр.4 вызова ПОИСК(v) обнаруживается, что вершина w "старая". Поэтому, добавив в процедуру ПОИСК(v) последнюю строку

9.       ИНАЧЕ   ПЕЧАТЬ(v,w),

мы получим процедуру, которая в дополнение построению к глубинного остова графа будет распечатывать список всех обратных ребер. Если этот список не пуст, то в графе имеются циклы, иначе - нет.

Поиск в глубину позволяет обнаруживать не только циклы, но и многие другие важные части графов.

Определение 11.3. Ребро (v,w) неориентированного графа G=(V,E) называется мостом G, если при его удалении из E число связных компонент графа увеличивается, т.е. в графе G'=(V, E \ { (v,w)} связных компонент больше, чем в G.

Из этого определения, в частности, следует, что ребро является мостом тогда и только тогда, когда оно не входит ни в какой цикл ( почему?). Поиск в глубину позволяет находить все мосты графа. Во-первых, заметим, что любой мост (v,w) является ребром глубинного остова, так как другого пути, связывающего v и w нет. Во-вторых, если это ребро ориентировано от v к w, то в глубинном остове нет обратных ребер, соединяющих w и его потомки с предками w. Это условие является и достаточным, так как, если таких ребер нет, то удаление (v,w) нарушит связь между v и w и они окажутся в разных компонентах связности. Обозначим через ВЕРХ(w) минимум из NUM[w] и наименьшего из номеров вершин, к которым ведут обратные ребра от вершин поддерева T_w. Тогда, учитывая, что обратные ребра соединяют потомков с предками и что номера предков меньше номеров потомков, предложенный критерий можно переформулировать в следующем виде.

Теорема 11.3. Ребро (v,w) глубинного остова D=(V,E) неориентированного графа G=(V,E) является мостом G тогда и только тогда, когда ВЕРХ(w) > NUM[v] или, что эквивалентно, ВЕРХ(w) = NUM[w].

Вычисление значения ВЕРХ(w) можно организовать в процессе обхода в глубину, используя следующее соотношение:

Для этого достаточно в строку 2 алгоритма ПОГ добавить начальное присвоение ВЕРХ(v) := NUM[v], в строке 7 приписать после ПОИСК(w) присвоение ВЕРХ(v) := min {ВЕРХ(v), ВЕРХ(w)}, учитывающее прямые ребра, и добавить строку

9.         ИНАЧЕ   ВЕРХ(v) := min{ВЕРХ(v),NUM(w)}

для учета обратных ребер.

Зная значения ВЕРХ(w), нетрудно выявить все мосты, используя критерий из теоремы 11.3.

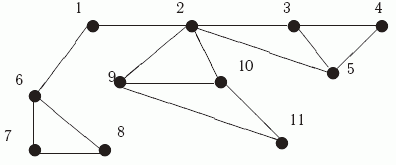
Пример 11.2. Применим алгоритм ПОГ к графу G₂, изображенному на рис. 11.3.

Рис. 11.3. Граф G2

Его представление в виде списков смежности имеет следующий вид:

Алгоритм ПОГ вызовет процедуру ПОИСК(1). Эта процедура рекурсивно вызовет ПОИСК(6) и т.д. Вот структура всех получающихся вызовов процедуры ПОИСК:

Вначале идут "горизонтальные" вызовы, затем возвраты справа налево и вызовы "по вертикали". В результате вершины G₂ получат следующие номера, отражающие порядок их прохождения:

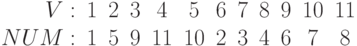
Ребра остова , построенные в процессе обхода графа, показаны на рис. 11.4. Стрелки указывают направление обхода. В скобках рядом с номером вершины указан ее номер в массиве NUM, т.е. номер в порядке обхода алгоритмом ПОГ.

Рис. 11.4. Остовное "глубинное" дерево S=(V,T) графа G2

В процессе построения этого дерева были определены следующие обратные ребра: (8,6), (10,2), (11,9), (5,2) и (4,3). Нетрудно проверить, что добавление любого из этих ребер к T приводит к образованию простого цикла.

Используя расширенный вариант ПОГ с вычислением функции ВЕРХ, мы получим следующий результат:

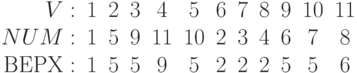
Так как ВЕРХ(2) =NUM[2] = 5 и ВЕРХ(6) =NUM[6] = 2, то по теореме 11.3 мостами графа G₂ являются ребра (1,2) и (1,6) и других мостов у него нет.

Алгоритм поиска в глубину часто используется как основа для различных алгоритмов обработки графов. Вместо строки 6, в котрой вершина v получает номер NUM(v), можно вставить вызов любой процедуры, обрабатывающей информацию, связанную с этой вершиной (например, для задачи о лабиринте это может быть проверка того, что v является выходом из лабиринта). И тогда полученный вариант алгоритма обеспечит обработку всех вершин графа.