НОУ ИНТУИТ | Введение в математику. Лекция 14: Элементы теории вероятностей и математической статистики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: платный | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать программу

Аннотация: Рассматриваются основные понятия теории вероятностей и математической статистики.

Ключевые слова: генеральной совокупностью, ПО, выборкой, выборка, случайная выборка, общей средней, средней по выборке, выборочной средней, анализ, средняя величина, средняя арифметическая характеристика, средневзвешенной оценкой, значение, Средняя гармоническая величина, Средняя квадратичная взвешенная величина, медиана, мода, ранжирование, прямой, обратный, коэффициент асимметрии, группа, Мера рассеяния, размах, среднее абсолютное отклонение, среднеквадратичное отклонение, дисперсия, стандартное отклонение, коэффициент вариации, группировка, потеря информации, Квантиль, Квартили, квартиль, децили, центили, процентили, число классов, групп, интервал, класс, середину класса, группы, Гистограмма, случайная величина, диаграмма, Абсциссой, ордината, Исход, Выборочное пространство, наблюдение, событие, пространство, испытание, испытания независимы, операции, объединение, пересечение, Дополнение, несовместимы, полную группу, противоположны, полная группа, частота события, вероятностью, предел, предел функции, подмножество, аксиома, Основные правила для вероятностей, условная вероятность, множество событий, вероятность, конечные, числовой функцией, дискретной случайной величиной, функция, дискретная случайная величина, распределение вероятности, математическим ожиданием, дисперсией, оценка математического ожидания, бесконечное множество, Распределение Бернулли, PQ, Биноминальное распределение, Распределение Пуассона, нормальное распределение, распределение Гаусса, интеграл, таблица, представление, неравенство, произвольное, неравенством Чебышева, место, законом больших чисел, параметр, гипотеза, эмпирическая формула, метод наименьших квадратов, регрессионными зависимостями, многофакторной регрессионной зависимостью

Элементы теории вероятностей и математической статистики

Пусть задан некоторый статистический ряд из элементов x₁, x₂,..., x_n. Если эти элементы могут принимать все мыслимые допустимые значения, а объект с этими характеристиками рассматривается как единый (как система), то такую совокупность называют генеральной совокупностью ; часто при этом предполагается (как и нами везде ниже), что она является конечной и упорядоченной по возрастанию: $x_1<x_2<\dotsc <x_n$ .

Любое непустое подмножество генеральной совокупности называется выборкой . Если выборка осуществлена случайным образом, то она называется случайной выборкой. Далее мы часто под выборкой будем понимать ранжированную, упорядоченную выборку.

Средняя величина генеральной совокупности в целом называется общей средней . Она отражает общие черты всей совокупности. Средняя величина для отдельной выборки называется средней по выборке или выборочной средней . Она отражает общие черты группы.

Основная цель статистических расчетов, как правило, состоит в том, чтобы по характеристикам выборки получить достоверную информацию о свойствах исходных генеральных совокупностей.

Пример. Повышение среднемесячной зарплаты, например, от 1200 руб. до 1500 руб. отражает лишь общую тенденцию динамики зарплаты (ее рост) по всем категориям трудящихся. В различных группах средние величины по группе могут сильно различаться, а в некоторых группах и не возрастать. Сравнительный анализ групповых и общих средних может дать информацию для характеристики социально-экономических слоев населения, о наличии и степени расслоения общества, о наличии и силе связей между групповым (факторным) признаком и результативным показателем.

Существуют различные меры средних величин.

Чаще используется средняя арифметическая характеристика:

$\bar x = \frac {\sum\limits^n_{i=1} x_i}{n} = \frac {x_1+x_2+\dotsc+ x_n}{n} .$

Она называется также выборочной средней или эмпирической средней.

Если измерения были неравноточными, или разной важности, то при вычислении средней арифметической характеристики используются весовые коэффициенты (например, отражающие точность измерения, инструмента) и такая средняя характеристика называется средневзвешенной оценкой . Она применяется также при вычислении общей средней (генеральной выборки) по выборочным средним (средним групп, выборок):

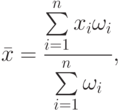
$\bar x = \frac {\sum\limits^n_{i=1} x_i\omega_i} {\sum\limits^n_{i=1} \omega_i},$

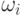где $\omega_i$ - веса (частоты).

При расчете средневзвешенных оценок по выборке важное значение имеет выбор веса и его обоснование. Средняя гармоническая величина, как и средняя арифметическая, может быть простой и взвешенной. Если все веса равны между собой, то можно использовать среднюю гармоническую в виде

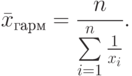
$\bar x_{\text{гарм}} = \frac {n}{\sum\limits^n_{i=1}\frac {1}{x_i} }.$

Средняя квадратичная взвешенная величина вычисляется по формуле

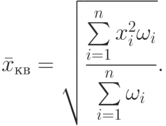
$\bar x_{\text{кв}} = \sqrt {\frac {\sum\limits^n_{i=1} x_i ^2\omega_i } {\sum\limits^n_{i=1} \omega_i } } .$

Если 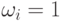$\omega_i=1$ для всех i=1,2,...,n, то получаем просто среднее квадратичное. Эти величины характеризуют "концентрацию" данных выборки около среднего (или другой характерной тенденции).

К средним величинам, которые характеризуют структурные изменения, относятся мода и медиана. Они определяются лишь структурой распределения, и их часто называют структурными средними (позиционными средними).

Мода - наиболее часто встречающееся значение признака у элементов данной совокупности. Она соответствует определенному значению признака. Мода может быть и не единственной.

Часто важно знать, где у выборки находится "центр" данных.

Медиана - значение признака, которое делит элементы ранжированной выборки на две равные части. Это середина ранжированного ряда. Если число элементов n - четно, то это среднее арифметическое двух средних элементов (хотя это значение может и не быть элементом ряда).

Для данных, имеющих "хорошее поведение", медиана всегда лежит в промежутке между средним арифметическим и модой. Эти величины выстраиваются по возрастанию следующим образом (напомним про упорядоченность по возрастанию выборки, предполагаемую нами для любого статистического ряда): среднее, медиана, мода, или же в обратном порядке. Прямой или обратный порядок их расположения можно определить, вычислив коэффициент асимметрии:

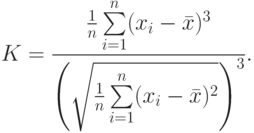
$K= \frac {\frac {1}{n}\sum\limits^n_{i=1} (x_i-\bar x)^3} {\Biggl(\sqrt{\frac {1}{n}\sum\limits^n_{i=1} (x_i-\bar x)^2} \Biggr) ^3}.$

Этот коэффициент (часто называемый третьим центральным моментом) отражает относительную изменчивость данных, их "поведение".

Группа оценок, называемых мерой рассеяния, разброса или вариацией, часто дает наиболее объективную характеристику.

Мера рассеяния - оценка, показывающая, как остальные элементы совокупности (выборки) группируются около средних величин.

Дальше >>

Введение в математику

Введение в математику

Элементы теории вероятностей и математической статистики

Элементы теории вероятностей и математической статистики

Вопросы и ответы

Студенты

Авторизоваться

Введение в математику

Введение в математику

Элементы теории вероятностей и математической статистики

Элементы теории вероятностей и математической статистики

Вопросы и ответы

Студенты