Практикум по алгоритмизации и программирования на Python

:

Практикум по алгоритмизации и программированию на Python
[+]
Опубликован: 05.04.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux
Лекция 3:

Графика в Python и задачи моделирования
A
|
версия для печати
< Лекция 2 || Лекция 3: 12 || Лекция 4 >

3.2 Пользовательские подпрограммы и моделирование. Модуль Tkinter

Гораздо более серьёзными возможностями, чем модуль turtle, обладает модуль Tkinter. Основное предназначение этого модуля — создание графических интерфейсов (GUI — Graphical User Interface) для программ на Python. Но благодаря наличию элемента графического интерфейса (или, как говорят, "виджета") canvas ("холст") Tkinter можно применять для рисования на основании координат, рассчитанных по формулам, используя доступные элементы векторной графики — кривые, дуги, эллипсы, прямоугольники и пр.

Рассмотрим задачу построения графика некоторой функции по вычисляемым точкам с помощью Tkinter.

Поскольку Tkinter позволяет работать с элементами GUI, создадим окно заданного размера, установим для него заголовок и цвет фона "холста", а также снабдим окно программной "кнопкой". На "холсте" определим систему координат и нарисуем "косинусоиду".

# -*- coding: utf-8 -*-

  import Tkinter

  import math

#
tk=Tkinter.Tk()
tk.title(" Sample ")
#
button=Tkinter.Button(tk)
button[" text "]="Закрыть"
button["command"]=tk.quit
button.pack()
#
canvas=Tkinter.Canvas(tk)
canvas["height"]=360
canvas["width"]=480
canvas["background"]="#eeeeff"
canvas["borderwidth"]=2
canvas.pack()
#
canvas.create_text(20, 10, text="2 0, 10")
canvas.create_text(460, 350, text="460, 350")
#
points=[]
ay=150
y0=150
x0=50
x1=470
dx=10
#

      for n in range(x0, x1, dx):

	y=y0-ay*math.cos(n*dx)
	pp=(n, y)
	points.append(pp)
#
canvas.create_line(points, fill="blue", smooth=1)
#
y_axe=[]
yy=(x0, 0)
y_axe.append(yy)
yy=(x0, y0+ay)
y_axe.append (yy)
canvas.create_line(y_axe, fill=" black ", width=2)
#
x_axe=[]
xx=(x0, y0)
x_axe.append(xx)
xx=(x1, y0)
x_axe.append(xx)
canvas.create_line(x_axe, fill=" black ", width=2)
#
tk.mainloop()
Окно Tkinter с кнопкой и графиком

Рис. 3.4. Окно Tkinter с кнопкой и графиком

Посмотрим на результат (рис. 3.4), и разберём текст примера.

Итак, первые три строки программы понятны — устанавливается кодовая страница и подключаются библиотеки. Поскольку в примере должны использоваться тригонометрические функции, необходимо подключить модуль math.

Затем создаётся так называемое "корневое" окно — говоря научным языком, "экземпляр интерфейсного объекта Tk", который представляет собой просто окно без содержимого. Для этого окна устанавливается значение свойства title (создаётся заголовок).

Далее начинается заполнение окна интерфейсными объектами ("виджетами" — widgets). В данном примере используется два объекта — кнопка и "холст". Для размещения объекта в окне используется метод pack(), а порядок объектов определяется порядком выполнения этой функции.

Кнопка создаётся как экземпляр объекта Button модуля Tkinter, связанный с "корневым" окном. Для кнопки можно установить текст надписи (свойство text) и связать кнопку с выполнением какой-либо команды (функции или процедуры), установив значение свойства command.

В приведённом примере кнопка связана с командой закрытия окна и прекращения работы интерпретатора, однако ничто не мешает также закрывать окно нашего "приложения" обычным образом — с помощью стандартной кнопки закрытия окна в верхнем правом углу.

После создания и размещения кнопки создаётся холст. Для элемента (объекта) canvas указываются высота, ширина, цвет фона и отступ от границ окна (таким образом, размеры окна получаются несколько больше, чем размеры объекта canvas). Размеры окна автоматически подстраиваются так, чтобы обеспечить размещение всех объектов (элементов интерфейса).

Прежде чем приступать к рисованию, исследуем систему координат. Поскольку размеры окна уже нами заданы, полезно определить, где находится точка с координатами (0, 0). Как видно из попыток вывести значения координат с помощью метода canvas.create_text(), начало координат находится в верхнем левом углу холста.

Теперь, определившись с координатами, можно выбрать масштабные коэффициенты и сдвиги и сформировать координаты точек для рисования кривой.

При использовании метода canvas. create_line() в качестве координат требуется список пар точек (кортежей) (x,y). Этот список формируется в цикле с шагом dx.

Для линии графика устанавливаются цвет и режим сглаживания. Сглаживание обеспечивает некоторую "плавность" кривой. Если его убрать, линия будет состоять из отрезков прямых. Кроме того, для линий можно устанавливать толщину, как это показано на примере осей координат.

3.2.1 Моделирование математических функций

Пусть требуется построить график функции, выбираемой из заданного списка. Здесь потребуется уже использование дополнительных интерфейсных элементов модуля Tkinter, а также создание собственных (пользовательских) процедур или функций для облегчения понимания кода.

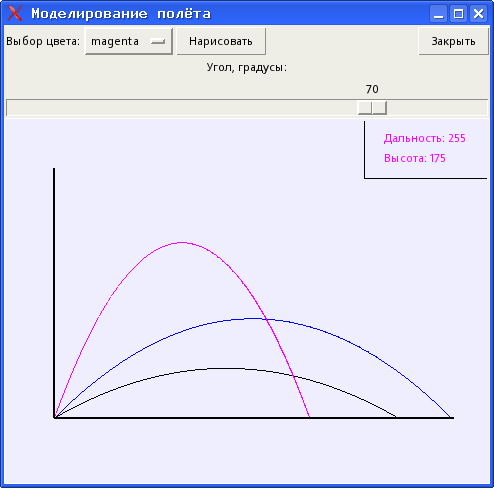
Результат решения задачи (вариант внешнего вида "приложения") показан на рис. 3.5.

Для выбора вида математической функции используется раскрывающийся список, после выбора вида функции и нажатия на кнопку "Нарисовать" на "холсте" схематически изображается график этой функции. Кнопка "Закрыть" закрывает наше "приложение". Теперь посмотрим на код.

# -*- coding: utf-8 -*-

  import Tkinter

  import math

#
# Пользовательские процедуры

  def plot_x_axe(x0, y0, x1):

	x_axe=[]
	xx=(x0, y0)
	x_axe.append(xx)
	xx=(x1, y0)
	x_axe.append(xx)
	canvas.create_line(x_axe, fill="black", width=2)
#

  def plot_y_axe(x0, y0, y1):

	y_axe=[]
	yy=(x0, y1)
	y_axe.append(yy)
	yy=(x0, y0)
	y_axe.append(yy)
	canvas.create_line(y_axe, fill="black", width=2)
#

  def plot_func0(x0, x1, dx, y0, y1):

	x0i=int(x0)
	x1i=int(x1)
	y0i=int(y0)
	y1i=int(y1)
	a=y1
	b=(y0-y1) / (x1-x0)
	points=[]

                for x in range(x0i, x1i, dx):

		y=int(a+b*x)
		pp=(x, y)
		points.append(pp)
		#
		canvas.create_line(points, fill="blue", smooth=1)
		plot_y_axe(x0i, y0i, y1i)
		plot_x_axe(x0i, y0i, x1i)
		#

  def plot_func1(x0, x1, dx, y0, y1):

	x0i=int(x0)
	x1i=int(x1)
	y0i=int(y0)
	y1i=int(y1)
	a=y0
	b=y0-y1
	points=[]

                for x in range(x0i, x1i, dx):

		y=int(a-y1i*b/ x)
		pp=(x, y)
		points.append(pp)
	#
	canvas.create_line(points, fill="blue", smooth=1)
	plot_y_axe(x0i, y0i, y1i)
	plot_x_axe(x0i, y0i, x1i)
#

  def plot_ func2(x0, x1, dx, y0, y1):

	x0i=int(x0)
	x1i=int(x1)
	y0i=int(y0)
	y1i=int(y1)
	a=(y0-y1)/(15*x1)
	b=1+((y0-y1)/(x1-x0))
	points=[]

                for x in range(x0i, x1i, dx):

		y=y0i-int(a*(x-x0i)**b)
		pp=(x, y)
		points.append(pp)
	#
	canvas.create_line(points, fill="blue", smooth=1)
	plot_y_axe(x0i, y0i, y1i)
	plot_x_axe(x0i, y0i, x1i)
#

  def plot_ func3(x0, x1, dx, y0, y1):

	x0i=int(x0)
	x1i=int(x1)
	y0i=int(y0)
	y1i=int(y1)
	ay=150
	y0i=150
	points=[]

                for x in range(x0i, x1i, dx):

		y=y0i-ay*math.cos(x*dx)
		pp=(x, y)
		points.append(pp)
	#
	canvas.create_line(points, fill="blue", smooth=1)
	plot_y_axe(x0i, 0, y0i+ay)
	plot_x_axe(x0i, y0i, x1i)
#

  def DrawGraph():

	fn=func.get()
	f=fn[0]
	x0=50.0
	y0=250.0
	x1=450.0
	y1=50.0
	dx=10
#

                if f=="0":

		canvas.delete("all")
		plot_ func0(x0, x1, dx, y0, y1)

                elif f=="1":

		canvas.delete("all")
		plot_ func1(x0, x1, dx, y0, y1)

                elif f=="2":

		canvas.delete("all")
		plot_ func2(x0, x1, dx, y0, y1)

                else:

		canvas.delete("all")
		plot_ func3(x0, x1, dx, y0, y1)
#
# Основная часть
tk=Tkinter.Tk()
tk.title(" Sample ")
# Верхняя часть окна со списком и кнопками
menuframe=Tkinter.Frame(tk)
menuframe.pack({"side":"top", "fill":"x"})
# Надпись для списка
lbl=Tkinter.Label(menuframe)
lbl["text"]="Выбор:"
lbl.pack({"side":"left"})
# Инициализация и формирование списка
func=Tkinter.StrigVar(tk)
func.set('0 y=Ax+B')
#
fspis=Tkinter.OptionMenu(menuframe, func,
	'0 y=Ax+B',
	'1 y=A+B/ x',
	'2 y=Ax^B',
	'3 y=A*cos(Bx)')
fspis.pack({"side":"left"})
# Кнопка управления рисованием
btnOk=Tkinter.Button(menuframe)
btnOk["text"]="Нарисовать"
btnOk["command"]=DrawGraph
btnOk.pack({"side":"left"})
# Кнопка закрытия приложения
button=Tkinter.Button(menuframe)
button["text"]="Закрыть"
button["command"]=tk.quit
button.pack({"side":"right"})
# Область рисования (холст)
canvas=Tkinter.Canvas(tk)
canvas["height"]=360
canvas["width"]=480
canvas["background"]="#eeeeff"
canvas["borderwidth"]=2
canvas.pack({"side":"bottom"})
tk.mainloop()
Построение графика для функции, выбираемой из списка

Рис. 3.5. Построение графика для функции, выбираемой из списка

Основная часть программы (интерфейсная) начинается с момента создания корневого окна (инструкция tk=Tkinter.Tk()). В этом окне располагаются два интерфейсных элемента — рамка (Frame) и холст (canvas). Рамка является "контейнером" для остальных интерфейсных элементов — текстовой надписи (метки — Label), раскрывающегося списка вариантов (OptionMenu) и двух кнопок. Как видно, кнопка закрытия стала объектом рамки, а не корневого окна, но по-прежнему закрывает всё окно.

Для получения нужного расположения элементов метод pack() используется с указанием, как именно размещать элементы интерфейса (к какой стороне элемента-контейнера их нужно "прижимать").

Есть некоторые тонкости в создании раскрывающегося списка. Для успешного выполнения этой операции нужно предварительно сформировать строку (а точнее, объект Tkinter.StringVar()) и определить для этого объекта значение по умолчанию (это значение будет показано в только что запущенном приложении). Затем при определении объекта OptionMenu() список значений дополняется. При выборе элемента списка изменяется значение именно этой строки и для дальнейшей работы нужно его анализировать, что и делается в процедуре DrawGraph().

"Вычислительная" часть, а именно, все процедуры и функции, обеспечивающие вычисления координат точек и рисование линий, вынесена в начало текста программы.

Определение каждой пользовательской подпрограммы обеспечивается составным оператором def. Поскольку эти подпрограммы занимаются только рисованием, они не возвращают никаких значений (т.е. результаты выполнения этих подпрограмм не присваиваются никаким переменным).

Собственно подпрограмма рисования графика DrawGraph() вызывается при нажатии кнопки "Нарисовать", и имя этой подпрограммы является командой, которая сопоставляется кнопке.

Эта подпрограмма берёт значение из списка (метод get()), выбирает первый символ получившейся строки и в зависимости от этого символа вызывает другие подпрограммы для построения конкретных графиков с установленными масштабными коэффициентами.

Перед рисованием следующего графика математической функции холст очищается командой canvas.delete("all").

Для построения графика каждой функции вычисляются собственные масштабные коэффициенты, поэтому их вычисление включено в код соответствующей подпрограммы. Кроме того, для графика нужны целые значения координат, поэтому в каждой подпрограмме выполняются соответствующие преобразования с помощью функции int().

Для каждого графика требуется нарисовать оси, и действия по рисованию осей также вынесены в отдельные подпрограммы.

Таким образом, оказывается, что программу нужно читать "с конца", и писать тоже.

3.2.2 Моделирование физического явления: тело, брошенное под углом к горизонту

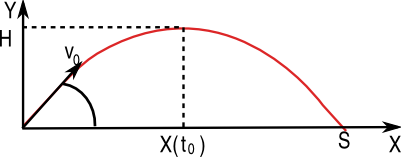
Теперь создадим небольшое приложение для моделирования движения тела, брошенного под углом к горизонту. Физическая задача формулируется следующим образом:

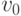Тело брошено под углом α к горизонту с начальной высоты h_0=0 и с начальной скоростью v_0. Определить величину угла α, при которой дальность полёта тела будет максимальной. Сопротивлением воздуха пренебречь.

Основные обозначения для решения задачи показаны на рис. 3.6.

Напишем формулы, по которым определяются координаты тела x и y в зависимости от времени.

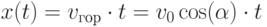x(t)=v_{гор}\cdot t=v_0\vdot \cos(\alpha)\cdot t ( 3.1)
Обозначения для задачи о теле, брошенном под углом к горизонту

Рис. 3.6. Обозначения для задачи о теле, брошенном под углом к горизонту
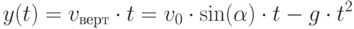y(t)=v_{верт}\cdot t=v_0\cdot \sin(\alpha)\cdot t - g\cdot t^2 ( 3.2)

Выразив время через координату x (на основании формулы

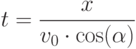t=\frac{x}{v_0\cdot \cos(\alpha)} ( 3.3)
и подставив выражение для времени в формулу для координаты y, получим уравнение траектории y(x):

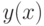y(x)=x\cdot \tg(\alpha) - x^2\cdot\frac{g}{2\cdot v^2_0\cdot \cos^2(\alpha)} ( 3.4)

Поскольку сопротивление при движении тела отсутствует, горизонтальная составляющая скорости изменяться не будет, а изменение вертикальной составляющей определяется влиянием ускорения свободного падения.

v_{гор}(t)=v_0\cdot \cos(\alpha) ( 3.5)
v_{верт}(t)=v_0\cdot \sin(\alpha) - g\cdot t ( 3.6)

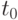Время t_0, через которое будет достигнута наивысшая точка траектории, найдём из условия v_{верт}=0.

t_0=\frac{v_0\cdot\sin(\alpha)}{g} ( 3.7)

Максимальную высоту подъёма H найдём из уравнения вертикального движения (формула 3.2) в момент времени t_0.

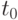H=y(t_0)=\frac{v^2_0\cdot\sin^2(\alpha)}{2\cdot g} ( 3.8)

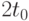Полное время полёта T очевидно, равно 2t_0, поэтому дальность полёта S определим как

S=v_{rop}\cdot T=v_0\cdot\cos(\alpha)\cdot 2\cdot t_0=\frac{v^2_0\cdot\sin^2(2\cdot\alpha)}{g} ( 3.9)

Все эти формулы понадобятся для вычисления координат точек траектории и параметров траектории при моделировании.

Текст программы с пользовательскими подрограммами приведён ниже.

# -*- coding: utf-8 -*
# Моделирование задачи о теле
# брошенном под углом к горизонту
#-

  import Tkinter

  import math

#

  def plot_x_axe(x0, y0, x1):

	x_axe=[]
	xx=(x0, y0)
	x_axe.append(xx)
	xx=(x1, y0)
	x_axe.append(xx)
	canvas.create_line(x_axe, fill="black", width=2)
#

  def plot_y_axe(x0, y0, y1):

	y_axe=[]
	yy=(x0, y1)
	y_axe.append(yy)
	yy=(x0, y0)
	y_axe.append(yy)
	canvas.create_line(y_axe, fill="black", width=2)
#

  def DrawGraph():

# Получаем и пересчитываем параметры
	dta=sc.get()
	alpha=dta_math.pi/180
	dtlbl=clist.get()
# Очищаем область для текста
	canvas.create_rectangle(x1i-90, y1i-50,
	x1i +50, y1i +10, fill="#eeeeff")
# Считаем g=10, v0 подбираем, чтобы всё влезало в canvas
	g=10.0
	v0=63
#
	S=int((v0**2)*math.sin(2*alpha)/g)
	H=int(((v0**2)*(math.sin(alpha))**2)/(2*g))
#
	points=[]

                for x in range(x0i, x1i):

		xx=(x-x0)
		y=(xx *math.tan(alpha))-((xx--2)-g/ \
			(2*(v0**2)*(math.cos(alpha)**2)))
#

                if y > 0 :

		yy=int(y0-y)

                else:

		yy=y0i
	#
		pp=(x, yy)
		points.append(pp)
# Собственно график
	canvas.create_line(points, fill=dtlbl, smooth=1)
	plot_x_axe(x0i, y0i, x1i)
# Параметры графика
	dtext="Дальность: "+str(S)
	vtext="Высота: "+str(H)
	dalnost=canvas.create_text(x1i-70, y1i-30, text=dtext,
		fill=dtlbl, anchor="w")
	vysota=canvas.create_text(x1i-70, y1i-10, text=vtext,
		fill=dtlbl, anchor="w")
#
# Основная часть
tk=Tkinter.Tk()
tk.title("Моделирование полёта")
# Верхняя часть окна со списком и кнопками
menuframe=Tkinter.Frame(tk)
menuframe.pack({"side":"top", "fill":"x"})
# Надпись для списка
lbl=Tkinter.Label(menuframe)
lbl["text"]="Выбор цвета:"
lbl.pack({"side":"left"})
# Инициализация и формирование списка
clist=Tkinter.StringVar(tk)
clist.set('black')
#
cspis=Tkinter.OptionMenu(menuframe, clist,
	'red',
	'green',
	'blue',
	'cyan',
	'magenta',
	'purple',
	'black')
cspis.pack({"side":"left"})
# Кнопка управления рисованием
btnOk=Tkinter.Button(menuframe)
btnOk["text"]="Нарисовать"
btnOk["command"]=DrawGraph
btnOk.pack({"side":"left"})
# Кнопка закрытия приложения
button=Tkinter.Button(menuframe)
button[" text "]="Закрыть"
button["command"]=tk.quit
button.pack({"side":"right"})
#
# Надпись для шкалы углов
lbl2=Tkinter.Label(tk)
lbl2["text"]="Угол, градусы:"
lbl2.pack({"side":"top"})
# Шкала углов
sc=Tkinter.Scale(tk, from_=0, to=90, orient="horizontal")
sc.pack({"side":"top", "fill":"x"})
#
# Область рисования (холст)
canvas=Tkinter.Canvas(tk)
canvas["height"]=360
canvas["width"]=480
canvas["background"]="#eeeeff"
canvas["borderwidth"]=2
canvas.pack({"side":"bottom"})
#
# Установки осей координат
x0=50.0
y0=300.0
x1=450.0
y1=50.0
#
x0i=int(x0)
x1i=int(x1)
y0i=int(y0)
y1i=int(y1)
# Оси координат
plot_x_axe(x0i, y0i, x1i)
plot_y_axe(x0i, y0i, y1i)
#
tk.mainloop()

Результат работы с моделью показан на рис. 3.7.

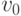Реализация модели имеет ряд особенностей. Во-первых, величина ускорения свободного падения g принята как 10. Во-вторых, модуль начальной скорости выбран так, чтобы при любых значениях угла вся траектория попадала в область графика. Не совсем правильно с точки зрения принципа разделения программ и данных установка значений для g и v_0 прямо в коде, но такое решение значительно упрощает работу с моделью.

Поиск угла для достижения максимальной дальности на модели

Рис. 3.7. Поиск угла для достижения максимальной дальности на модели

"Ползунок" на шкале установки углов показывает значения в градусах, а для правильных вычислений в тригонометрических функциях эти значения нужно перевести в радианы.

Высота и дальность полёта пишутся для каждой траектории соответствующим цветом в прямоугольнике в верхнем правом углу. Для каждой следующей траектории этот прямоугольник рисуется заново и текст переписывается.

В этой главе рассмотрены лишь некоторые базовые возможности модуля Tkinter и использования Python для создания моделей. Если возникнет желание более подробно познакомиться с применением объектом и методов этого модуля, можно изучить оригинальную документацию и другие примеры, используя ресурсы Интернет.

3.2.3 Задачи и упражнения

  1. Для примера, показанного на рис. 3.4, нанесите на оси метки и проставьте значения в масштабе графика.
  2. Напишите подпрограмму формирования строки со значениями координат для примера, показанного на рис. 3.2.
  3. Напишите подпрограммы для нанесения меток и вывода значений по горизонтальной и вертикальной осям для примера моделирования математических функций.
  4. В модели тела, брошенного под углом у горизонту, напишите подпрограммы вывода метки "точки падения" и метки максимальной высоты для каждой траектории.
  5. Модифицируйте код для моделирования полёта так, чтобы можно было изменять начальную скорость, а график автоматически масштабировался в области рисования.
Дальше >>
< Лекция 2 || Лекция 3: 12 || Лекция 4 >

Вопросы и ответы

вопросов: 3
Ольга Курыло
Ольга Курыло
ответить
Александр Кудлаев
Александр Кудлаев

Ознакомился с курсом "Практика по алгоритмизации и программированию на Python". Хотел сдать экзамен. Вместо традиционного тестирования было предложено написать курсовую работу. Написал. Отослал.Ответ на следующий день: "Задание не прверено". Сколько ожидать результата проверки работы?

ответить

Студенты

всего: 106
Pavel Kucharenka
Pavel Kucharenka
предложить дружбу
Шавкатжон Кодиров
Шавкатжон Кодиров
Узбекистан, Ташкент
предложить дружбу