| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Графический метод оптимизации линейных моделей
Задача 1.1. Выпуск продукции
Фирма производит две модели  и
и  сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем
машинной обработки. Для каждого изделия модели
сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем
машинной обработки. Для каждого изделия модели  требуется
требуется  досок, а для модели
досок, а для модели  —
—  .
Фирма может получать от своих поставщиков до
.
Фирма может получать от своих поставщиков до
 досок в неделю. Для каждого изделия модели
досок в неделю. Для каждого изделия модели  требуется 12 мин. машинного времени, а для изделия модели
требуется 12 мин. машинного времени, а для изделия модели  — 30 мин.
В неделю можно использовать 160 часов машинного времени.
— 30 мин.
В неделю можно использовать 160 часов машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю, если каждое изделие модели  приносит 200 руб. прибыли, а
каждое изделие модели
приносит 200 руб. прибыли, а
каждое изделие модели  — 400 руб. прибыли?
— 400 руб. прибыли?
В данном случае объектом является фирма, а ее деятельность представляется в виде математической модели, т.е. учитываются только некоторые количественные стороны этой деятельности. Менеджер (субъект) ставит себе задачу: составить недельный производственный план фирмы. При этом он руководствуется целью моделирования — максимальной эффективностью производства, получением максимальной прибыли.
Построение математической модели
Пусть  - количество выпущенных за неделю полок модели
- количество выпущенных за неделю полок модели  , а
, а  — количество выпущенных за неделю полок
модели
— количество выпущенных за неделю полок
модели  .
Тогда составим следующие соотношения:
.
Тогда составим следующие соотношения:
 - количество досок, требуемых на неделю для изготовления полок модели
- количество досок, требуемых на неделю для изготовления полок модели  .
.
 - количество досок, требуемых на неделю для изготовления полок модели
- количество досок, требуемых на неделю для изготовления полок модели  .
.
 - количество досок требуемых на неделю для изготовления книжных полок двух моделей.
По условию задачи это число не должно превышать
- количество досок требуемых на неделю для изготовления книжных полок двух моделей.
По условию задачи это число не должно превышать  , следовательно, получаем первое ограничение:
, следовательно, получаем первое ограничение:
 |
( 1) |
Найдем ограничение на использование машинного времени.
12 мин. составляют 0,2 часа, а 30 мин. — 0,5 часа, таким образом:
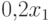 - количество времени, требуемое на неделю для обработки полок модели
- количество времени, требуемое на неделю для обработки полок модели  ;
;
 - количество времени, требуемое на неделю для обработки полок модели
- количество времени, требуемое на неделю для обработки полок модели  ;
;
 - количество времени, требуемое на неделю для обработки двух моделей. По условию задачи это число не должно
превышать 160 часов,
следовательно, получаем второе ограничение:
- количество времени, требуемое на неделю для обработки двух моделей. По условию задачи это число не должно
превышать 160 часов,
следовательно, получаем второе ограничение:
 |
( 2) |
 |
( 2) |
Кроме того, поскольку  и
и  выражают еженедельный объем выпускаемых изделий, то они не могут
быть отрицательными, то есть
выражают еженедельный объем выпускаемых изделий, то они не могут
быть отрицательными, то есть
 |
( 3) |
Наша задача состоит в том, чтобы найти такие значения  и
и  , при которых еженедельная прибыль
будет максимальной.
Составим выражение для еженедельной прибыли:
, при которых еженедельная прибыль
будет максимальной.
Составим выражение для еженедельной прибыли:
 - еженедельная прибыль, получаемая от продажи полок модели
- еженедельная прибыль, получаемая от продажи полок модели  .
.
 - еженедельная прибыль, получаемая от продажи полок модели
- еженедельная прибыль, получаемая от продажи полок модели  .
.
 - еженедельная прибыль, которая должна быть максимальной.
- еженедельная прибыль, которая должна быть максимальной.
Таким образом, имеем следующую математическую модель для данной задачи:
 ;
;
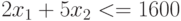 ;
;
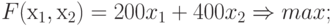
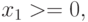
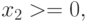
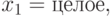

Необходимо найти значения переменных  и
и  , при которых данная функция
, при которых данная функция  принимает
максимальное значение, при соблюдении ограничений, накладываемых на эти переменные.
принимает
максимальное значение, при соблюдении ограничений, накладываемых на эти переменные.
Решения, удовлетворяющие системе ограничений и требованию неотрицательности, являются допустимыми, а решения, удовлетворяющие одновременно и требованию максимизации (минимизации) целевой функции являются оптимальными.
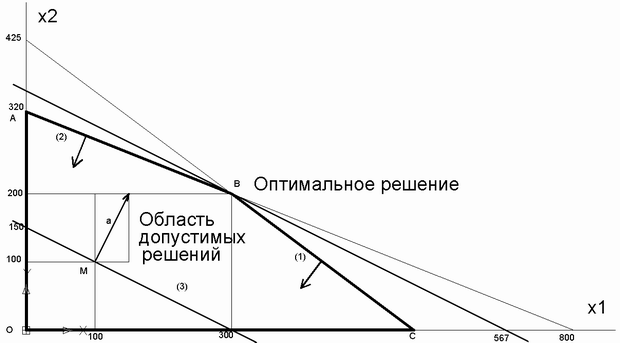
Область допустимых решений целевой функции
 можно найти графическим методом.
можно найти графическим методом.
Построим прямоугольную систему координат, где по оси  отложим значения
отложим значения  , а по оси
, а по оси 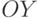 отложим значения
отложим значения
 . Так как, согласно условию (3),
. Так как, согласно условию (3),  и
и  неотрицательны, то можно ограничиться рассмотрением первого
квадранта (рисунок 1.2).
неотрицательны, то можно ограничиться рассмотрением первого
квадранта (рисунок 1.2).
Рассмотрим первое ограничение:

Заменим в данном ограничении знак неравенства знаком равенства и построим прямую

Для этого найдем две точки, принадлежащие данной прямой. Пусть,
например,  ,
, 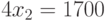 или
или 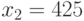 .
.  — координаты первой точки, принадлежащей прямой.
— координаты первой точки, принадлежащей прямой.
Пусть 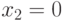 , то
, то  , следовательно,
, следовательно,  .
.
 — координаты второй точки, принадлежащей прямой. Отметим эти точки на числовых осях.
— координаты второй точки, принадлежащей прямой. Отметим эти точки на числовых осях.
Аналогично, для второго ограничения:
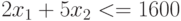

При  ,
, 
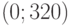
При 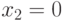 ,
, 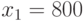

Построим данные прямые (на рисунке они соответственно обозначены (1) и (2))
Теперь найдем на чертеже такие полуплоскости, которые соответствуют неравенствам (1) и (2). Прямая (1) делит координатную плоскость на две полуплоскости. Одна полуплоскость расположена выше прямой, вторая ниже. Чтобы найти ту полуплоскость, которая соответствует неравенству (1), необходимо взять любую точку, принадлежащую одной из полуплоскостей и подставить ее координаты в неравенство. Если неравенство будет верным, то данная полуплоскость является искомой.
Например, возьмем точку с координатами  и подставим ее координаты в неравенство (1)
и подставим ее координаты в неравенство (1)  .
Получается
.
Получается 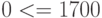 - данное неравенство является верным, следовательно, неравенству (1) удовлетворяет полуплоскость,
лежащая ниже прямой (1).
- данное неравенство является верным, следовательно, неравенству (1) удовлетворяет полуплоскость,
лежащая ниже прямой (1).
Аналогично, поступим для неравенства (2)  . Возьмем точку с координатами
. Возьмем точку с координатами  .
Получается
.
Получается 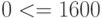 - данное неравенство верно. Неравенству (2) удовлетворяет полуплоскость, расположенная ниже прямой (2).
Стрелки на каждой границе показывают, с какой стороны прямой выполнены ограничения. Учитывая неравенства (3), получаем, что
выделенный четырехугольник
- данное неравенство верно. Неравенству (2) удовлетворяет полуплоскость, расположенная ниже прямой (2).
Стрелки на каждой границе показывают, с какой стороны прямой выполнены ограничения. Учитывая неравенства (3), получаем, что
выделенный четырехугольник  является областью, содержащей точки, для которых выполнены условия (1-3). Точки, лежащие внутри и
на границе этой области, являются допустимыми решениями. Среди всех допустимых решений нужно найти
оптимальное решение, при котором
функция
является областью, содержащей точки, для которых выполнены условия (1-3). Точки, лежащие внутри и
на границе этой области, являются допустимыми решениями. Среди всех допустимых решений нужно найти
оптимальное решение, при котором
функция  будет принимать максимальное значение.
будет принимать максимальное значение.
Для поиска оптимального решения построим по функции  прямую уровня.
прямую уровня.
Возьмем произвольную точку, принадлежащую области допустимых решений — четырехугольнику
 , например, точку
, например, точку  с координатами
с координатами 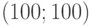 .
Подставим координаты точки
.
Подставим координаты точки  в функцию
в функцию  .
.
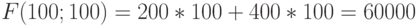
Прямая уровня будет иметь следующий вид: 
Построим полученную прямую. Для этого необходимо найти координаты двух произвольных точек этой прямой. Одна точка у нас уже есть — это
точка 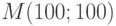 . Найдем еще одну точку. Пусть
. Найдем еще одну точку. Пусть 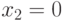 , тогда
, тогда 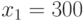 . Следовательно, координаты дополнительной
точки
. Следовательно, координаты дополнительной
точки  .
Отметим полученные точки и построим прямую уровня (на рисунок 1.2 она обозначена (3)).
.
Отметим полученные точки и построим прямую уровня (на рисунок 1.2 она обозначена (3)).
Значения функции  будут возрастать по мере того, как прямая уровня удаляется от начала координат в положительном квадранте.
Направление возрастания функции
будут возрастать по мере того, как прямая уровня удаляется от начала координат в положительном квадранте.
Направление возрастания функции  будет совпадать с вектором, координаты которого являются коэффициентами при
переменных
будет совпадать с вектором, координаты которого являются коэффициентами при
переменных  и
и  функции
функции  . На рисунке — это вектор
. На рисунке — это вектор  , отложенный от точки
, отложенный от точки  .
Обратите внимание, что вектор
.
Обратите внимание, что вектор  , определяющий направление возрастания функции
, определяющий направление возрастания функции  , всегда будет перпендикулярен прямой
уровня.
, всегда будет перпендикулярен прямой
уровня.
Максимизация целевой функции 
Для нахождения точки, в которой функция  достигнет своего максимального значения, необходимо перемещать прямую уровня по
направлению
вектора
достигнет своего максимального значения, необходимо перемещать прямую уровня по
направлению
вектора  до пересечения этой прямой с граничной точкой области допустимых решений. На нашем рисунке — это точка В.
до пересечения этой прямой с граничной точкой области допустимых решений. На нашем рисунке — это точка В.
Найдем координаты точки  . Данная точка расположена на пересечении двух прямых (1) и (2), поэтому, чтобы найти ее координаты необходимо
решить следующую систему уравнений:
. Данная точка расположена на пересечении двух прямых (1) и (2), поэтому, чтобы найти ее координаты необходимо
решить следующую систему уравнений:
 ;
;
 .
.
Легко убедиться, что оптимальное решение этой задачи задается в вершине выпуклого четырехугольника координатами
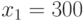 ;
;  .
.
Значит, чтобы получить максимальную прибыль  руб., фирме
необходимо выпускать в неделю триста полок модели
руб., фирме
необходимо выпускать в неделю триста полок модели  и двести полок модели
и двести полок модели  .
.