| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Инспектор
Вы можете этот курс.
Опубликован: 14.11.2012 | Уровень: для всех | Доступ: платный
Лекция 1:
Графический метод оптимизации линейных моделей
Аннотация: Задачи линейного программирования с линейной целевой функцией и линейными ограничениями можно решать аналитическими и графическими методами.
Аналитические методы представляют собой последовательность вычислений по некоторым правилам.
Они являются основой для решения задачи на компьютере.
Ключевые слова: слово, программирование, математическая модель, максимум, целевая функция, Произведение, вектор, коэффициенты, метод решения, значение, интерпретация, ПО, симплекс, фирма, деятельность, менеджер, прибыль, выражение, функция, прямой, координаты, плоскость, неравенство, минимум, область допустимых значений, расстояние, оптимальное решение, оптимизация, excel, симплекс-метод, алгоритм, линейное программирование, поиск, анализ решения, работ, пункт, ресурс, матрица, отладка, программа, анализ, мера, область допустимых решений
Цель лекции: Показать возможность графического решения задач с двумя неизвестными.
Математическое программирование занимается исследованием детерминированных и одноцелевых задач. Слово "программирование" в данном случае означает "планирование". К математическому программированию относится:
- Линейное программирование: нахождение экстремального значения линейной функции многих переменных при наличии линейных ограничений, связывающих эти переменные.
- Нелинейное программирование:целевая функция и ограничения могут быть нелинейными функциями.
- Целочисленное программирование: особый случай в задачах линейного и нелинейного программирования, когда на оптимальные решения накладывается условие целочисленности искомых параметров.
- Динамическое программирование: для отыскания оптимального решения планируемая операция разбивается на ряд шагов (этапов) и планирование осуществляется последовательно от этапа к этапу. Однако выбор метода решения на каждом этапе производится с учетом интересов операции в целом.
- Теория графов, с помощью которой решаются многие сетевые задачи, связанные с минимальным протяжением сети, построение кольцевого маршрута и т.д.
Математическая модель любой задачи линейного программирования включает в себя:
- набор констант, характеризующих, например, наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы;
- искомые переменные величины, например, количество запланированной к выпуску продукции по всему ассортименту;
- максимум или минимум целевой функции, например, запланированной прибыли;
- систему ограничений в форме линейных уравнений и неравенств, например, условие того, что расход материала не должен превышать его запас;
- требование неотрицательности переменных (если не предусмотрено иное).
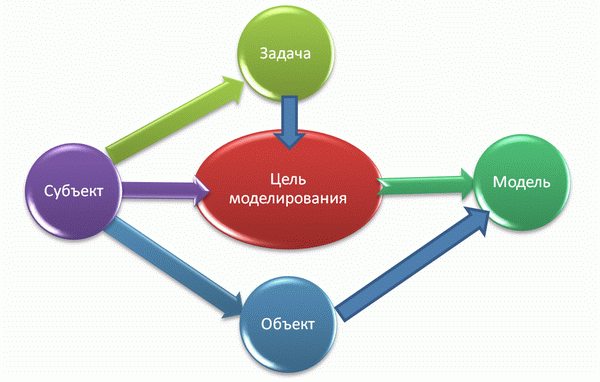
Решение практической задачи всегда связано с исследованием, с преобразованием некоторого объекта (материального или информационного) или с управлением им (рисунок 1.1).
При решении "стандартной" задачи в линейном программировании нужно определить максимум линейной целевой функции
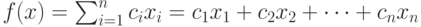
при условиях
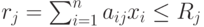
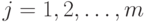
Здесь целевая функция формируется как скалярное произведение двух векторов. Один из них — вектор
искомых переменных 
.
Компонентами другого вектора являются целевые коэффициенты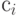 
. Условия задачи можно сформулировать так: "Расход
не должен превышать имеющиеся ресурсы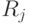 
".
Вектор расхода есть сумма произведений матрицы нормированных коэффициентов 
на вектор
искомых переменных .
Основной аналитический метод решения задач линейного программирования — это симплексный метод . Он сводится к вычислительной процедуре, основанной на принципе последовательного улучшения решений — перехода от одной базисной точки к другой, для которой значение целевой функции больше. Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов. Геометрическая интерпретация метода состоит в последовательном движении по вершинам симплекса (n-мерного тетраэдра). Симплекс-метод послужил исходным пунктом для разработки целого семейства алгоритмов решения как линейных, так и нелинейных выпуклых задач оптимизации.
Никита Козлов
