Поле C комплексных чисел
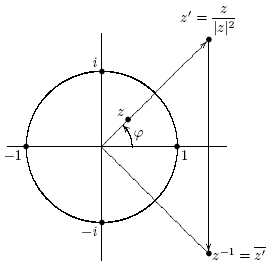
Геометрическая интерпретация обратного элемента
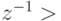 для
для 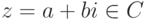
Если  , то, как мы видели, zz=N(z)=|z|2=a2+b2,
, то, как мы видели, zz=N(z)=|z|2=a2+b2,
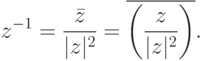
а) инверсия  относительно окружности единичного радиуса (
относительно окружности единичного радиуса (  );
);
б) сопряжение 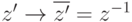 .
.
Задача 2.8.1. Найти геометрическое множество точек z-1, где z пробегает прямую 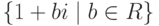 .
.
Упражнение 2.8.2.
Для 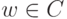 ,
,  , имеем
, имеем
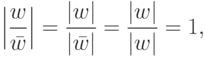

Если 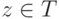 , т. е. |z|=1,
, т. е. |z|=1, 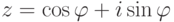 , то
, то 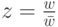 для некоторого
для некоторого 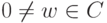 . Таким образом,
. Таким образом,

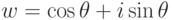 , то
, то  и
и
 , т. е.
, т. е. 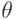 , то
, то  является одним из решений этой задачи.
является одним из решений этой задачи.Упражнение 2.8.3.
- Единичная окружность
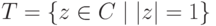 с операцией умножения является группой (подгруппой мультипликативной группы
с операцией умножения является группой (подгруппой мультипликативной группы 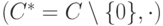 поля C комплексных чисел).
поля C комплексных чисел). -
 .
. - Найти все
 , для которых
, для которых 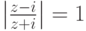 .
. - Найти все
 , для которых |z+i|+|z-i|=2.
, для которых |z+i|+|z-i|=2. - Три различных комплексных числа
 лежат на одной прямой в R2 тогда и только тогда, когда
лежат на одной прямой в R2 тогда и только тогда, когда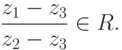
- Четыре различных комплексных числа
 , не лежащие на одной прямой в R2, лежат на одной окружности тогда и только тогда, когда их двойное отношение является вещественным числом:
, не лежащие на одной прямой в R2, лежат на одной окружности тогда и только тогда, когда их двойное отношение является вещественным числом: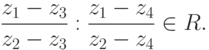
- Рассмотрим отображение инфлексии
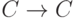 ,
,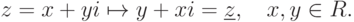
Показать, что:
(a) отображение
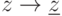 является биекцией, при этом
является биекцией, при этом 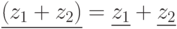 ,
,  ;
;(б)
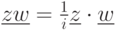 для
для  ;
;(в)
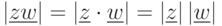 , в частности
, в частности  для
для  .
.
Теорема 2.8.4 (формула Муавра о возведении в степень комплексного числа в тригонометрической форме). Пусть 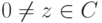 ,
, 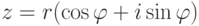 , r>0,
, r>0,  . Тогда
. Тогда
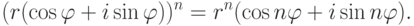
Доказательство. Утверждение теоремы - частный случай теоремы 2.7.1.
Упражнение 2.8.5. Так как для 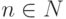

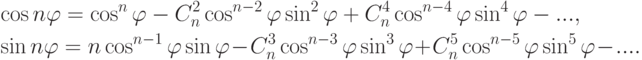
Например:
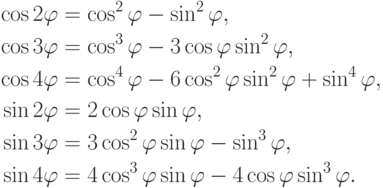
Упражнение 2.8.6. Если
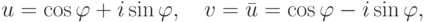
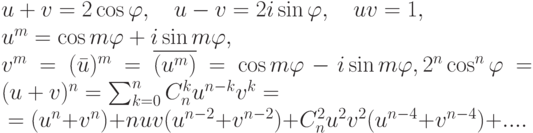
Если n=2k, то
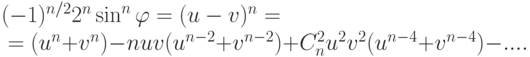
Если n=2k+1, то
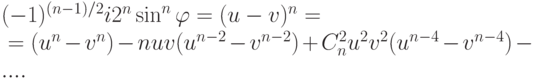
Отсюда: если n=2k, то
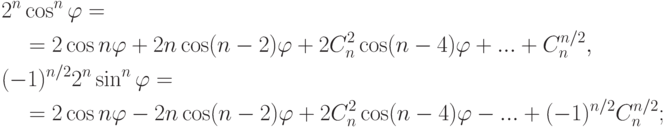
если n=2k+1, то
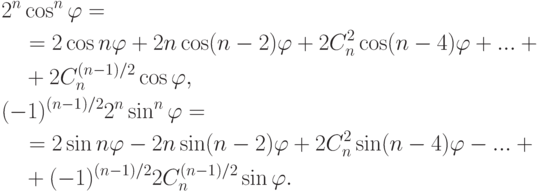
Упражнение 2.8.7. Если 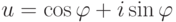 ,
, 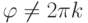 , то
, то
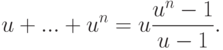
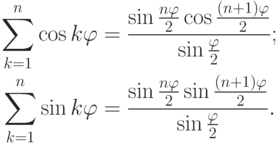
Теорема 2.8.8 (извлечение корней n-й степени из комплексных чисел). Пусть  ,
, 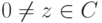 ,
,  , r>0. Тогда существует ровно n различных корней n -й степени из z )таких
, r>0. Тогда существует ровно n различных корней n -й степени из z )таких 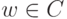 , что wn=z ) :
, что wn=z ) :
![w_k=\sqrt[n]{r}\left(\cos\frac{\varphi\!+\!2\pi k}{n}+ i\sin\frac{\varphi\!+\!2\pi k}{n}\right),\ k=0,1,2,...,n-1.](/sites/default/files/tex_cache/433f02094a8e5fef97f22862572c63b9.png)
![\rho=\sqrt[n]{r}](/sites/default/files/tex_cache/1c657e1b45d2636dd706218cc62544db.png) , образуя вершины правильного
, образуя вершины правильного  -угольника с аргументами
-угольника с аргументами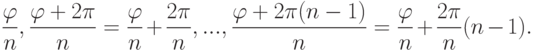
Доказательство. Будем искать решения w уравнения wn=z в тригонометрической форме:
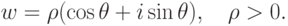

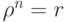 , и поэтому
, и поэтому ![\rho=\sqrt[n]{r}](/sites/default/files/tex_cache/1c657e1b45d2636dd706218cc62544db.png) ,
, 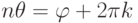 ,
,  . Различных корней будет ровно n при k=0,1,2,...,n-1:
. Различных корней будет ровно n при k=0,1,2,...,n-1:![w_k=\sqrt[n]{r}\left(\cos\frac{\varphi+2\pi k}{n}+ i\sin\frac{\varphi+2\pi k}{n}\right),\quad k=0,1,2,...,n-1.](/sites/default/files/tex_cache/0fc3e671a3d0b988529238bb52e45265.png)
Упражнение 2.8.9. Найдем корни уравнения x2-(2+i)x+(-1+7i)=0 (в алгебраической форме):
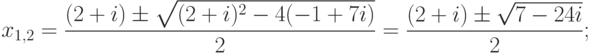
 ,
,  , где
, где 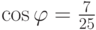 ,
,  ,
,  . Так как
. Так как 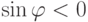 ,
,  , то
, то 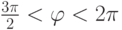 , и поэтому
, и поэтому  , т. е.
, т. е.  ,
, 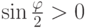 , следовательно,
, следовательно, 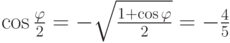 ,
, 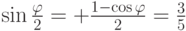 ,
, 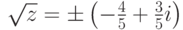 . Итак,
. Итак,  , x1=-1+2i, x2=3-i.
, x1=-1+2i, x2=3-i.Упражнение 2.8.10. Найти все корни третьей степени из  . По формуле из теоремы все три корня из
. По формуле из теоремы все три корня из 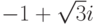 имеют следующий вид:
имеют следующий вид:
![\begin{gat}
w_0 = \sqrt[3]{2}\left(\cos\frac{2\pi}{9}+i\sin\frac{2\pi}{9}\right);\\
w_1 = \sqrt[3]{2}\left(\cos\frac{8\pi}{9}+i\sin\frac{8\pi}{9}\right);\quad
w_2 = \sqrt[3]{2}\left(\cos\frac{14\pi}{9}+i\sin\frac{14\pi}{9}\right).
\end{gat}](/sites/default/files/tex_cache/20dcf07f368649dfafca793a7dc19810.png)
Упражнение 2.8.11. Найти все корни четвертой степени из i. Так как  , по формуле из теоремы все четыре корня из i имеют следующий вид:
, по формуле из теоремы все четыре корня из i имеют следующий вид:
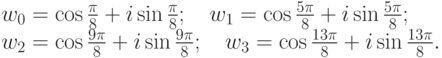
Упражнение 2.8.12. Извлеките все корни
![\sqrt[6]{\frac{1-i}{\sqrt{3}+i}}.](/sites/default/files/tex_cache/12b909f38d4af59ac50398c7c6fc9d66.png)
Упражнение 2.8.13. Покажите, что
![\sqrt[4]{-\frac{18}{1+i\sqrt{3}}}= \biggl\{\pm\biggl(\frac{3}{2}+i\frac{\sqrt{3}}{2}\biggr), \pm\biggl(\frac{\sqrt{3}}{2}-\frac{3}{2}i\biggr)\biggr\}.](/sites/default/files/tex_cache/dfefd36cd511b6bfa9d882f199303f6d.png)