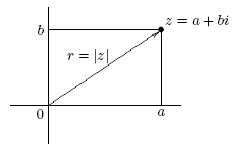
Поле C комплексных чисел
Сопряжение комплексных чисел
Каждому комплексному числу 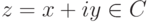 сопоставим комплексное число
сопоставим комплексное число 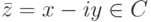 , называемое комплексно сопряженным. Геометрическая интерпретация перехода от z=a+bi к сопряженному комплексному числу z=a-bi прозрачна: это отражение относительно вещественной оси:
, называемое комплексно сопряженным. Геометрическая интерпретация перехода от z=a+bi к сопряженному комплексному числу z=a-bi прозрачна: это отражение относительно вещественной оси:
Теорема 2.3.1.
- Операция комплексного сопряжения
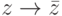 является автоморфизмом поля C комплексных чисел (т. е. биекцией, для которой
является автоморфизмом поля C комплексных чисел (т. е. биекцией, для которой  ,
, 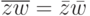 для
для  и, как следствие,
и, как следствие, 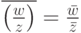 для
для 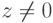 ), оставляющим все действительные числа и только их на месте ( a=a для
), оставляющим все действительные числа и только их на месте ( a=a для 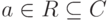 ; если z=z, то
; если z=z, то 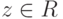 ).
). - Квадрат комплексного сопряжения равен тождественному отображению (
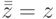 ).
). - Если
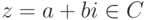 ,
,  , то
, то 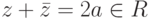 ,
, 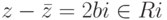 ,
, 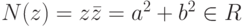 , при этом N(wz)=N(w)N(z) для
, при этом N(wz)=N(w)N(z) для 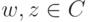 .
. - Если
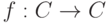 - такой автоморфизм поля C комплексных чисел, что f(a)=a для всех
- такой автоморфизм поля C комплексных чисел, что f(a)=a для всех 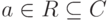 , то либо f=1C, либо
, то либо f=1C, либо 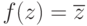 для
для  (тем самым показано, что группа Галуа расширения
(тем самым показано, что группа Галуа расширения  состоит из двух элементов).
состоит из двух элементов).
Доказательство.
- Ясно, что соответствиеявляется биекцией.
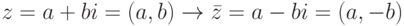
Если z=a+bi, w=c+di, то z+w = (a+b)+(c+d)i=(a+b)-(c+d)i= =(a-ci)+(b-di)=z+w; -z=-a-bi=-a+bi=-(a-bi)=-(z); z-w=z+(-w)=z-w; zw=(ac-bd)+(ad+bc)i=(ac-bd)-(ad+bc)i= =(a-bi)(c-di)=zw.
Если
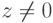 , то
, то 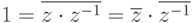 , т. е.
, т. е. 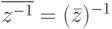 . Поэтому
. Поэтому
Если
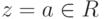 , то z=a. Если z=a+bi, то z=z означает, что z=a+bi=a-bi=z, т. е. b=-b, поэтому b=0 и
, то z=a. Если z=a+bi, то z=z означает, что z=a+bi=a-bi=z, т. е. b=-b, поэтому b=0 и 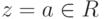 . Итак, z=z тогда и только тогда, когда
. Итак, z=z тогда и только тогда, когда 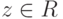 .
. -
 .
. - Если z=a+bi, тоДалее,
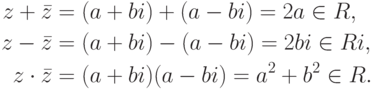

- Так как i2=-1, то f(i)^2=f(-1)=-1, поэтому
либо f(i)=i, и тогда f(a+bi)=f(a)+f(b)f(i)=a+bi },
либо f(i)=-i, и тогда f(a+bi)=f(a)+f(b)f(i)=a-bi
Замечание 2.3.2.
- Если комплексное число
 получено как выражение из комплексных чисел
получено как выражение из комплексных чисел 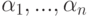 с помощью операций сложения, вычитания, умножения и деления, то то же выражение из комплексных чисел
с помощью операций сложения, вычитания, умножения и деления, то то же выражение из комплексных чисел 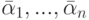 дает
дает  .
. - Правило деления комплексного числа w=c+di на ненулевое комплексное число
 (в алгебраической форме):
(в алгебраической форме):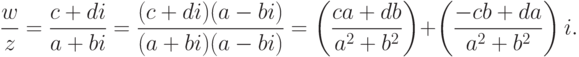
Полярные координаты точек плоскости (отличных от начала координат)
Точка плоскости (a,b), отличная от начала координат (0,0), однозначно задается своими полярными координатами r,  , где r - расстояние от данной точки до начала координат,
, где r - расстояние от данной точки до начала координат,  - угол между положительной полуосью абсцисс и радиусом-вектором точки (a,b), отсчитываемый против часовой стрелки (определенный с точностью до
- угол между положительной полуосью абсцисс и радиусом-вектором точки (a,b), отсчитываемый против часовой стрелки (определенный с точностью до  ,
, 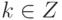 , и называемый аргументом точки (a,b) ).
, и называемый аргументом точки (a,b) ).
Аргумент точки 0=(0,0) не определен.
Формулы перехода от декартовых координат a и b точки (a,b) к полярным координатам и обратно:
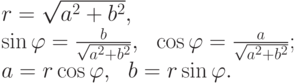
Свойства модуля комплексных чисел
Для комплексного числа 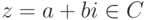 определим его модуль как
определим его модуль как
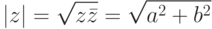
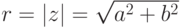 - это расстояние от точки (0,0) до точки (a,b), т. е. длина вектора z ).
- это расстояние от точки (0,0) до точки (a,b), т. е. длина вектора z ).Пример 2.5.1.
- Если
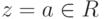 , то
, то  , т. е. функция модуль комплексного числа
, т. е. функция модуль комплексного числа 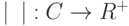 является продолжением функции модуль действительного числа
является продолжением функции модуль действительного числа 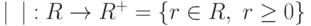 .
. -
|i|=1,
 .
. -
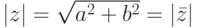 для
для 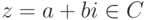 .
. -
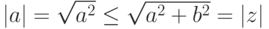 для
для 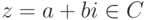 .
.
Лемма 2.5.2. |wz|=|w|*|z| для 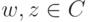 .
.
Доказательство.

Другое доказательство этого факта следует из свойств тригонометрической формы.
Следствие 2.5.3.
- Если w=z-1 для
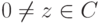 , то 1=|1|=|z-1z|=|z-1|,|z|, поэтому
, то 1=|1|=|z-1z|=|z-1|,|z|, поэтому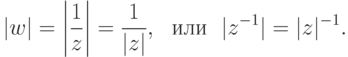
- Для
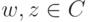 ,
, 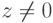 :
: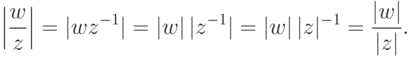
Лемма 2.5.4.  для
для 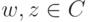 .
.
Первое доказательство. Длина |w+z| стороны треугольника не превосходит суммы длин |w|+|z| двух других сторон.
Второе доказательство. Если w=0 или z=0, то утверждение очевидно.
Пусть теперь  и
и 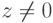 . Так как для z=a+bi имеем
. Так как для z=a+bi имеем

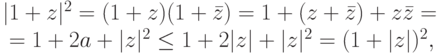
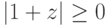 ,
, 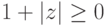 ,
,  . Далее,
. Далее,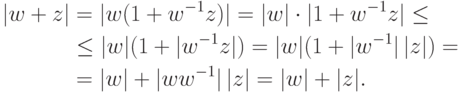
Следствие 2.5.5.  для
для 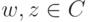 .
.
Доказательство.
-
 .
. - Так как
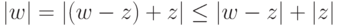 , то
, то  .
. -
 .
.