НОУ ИНТУИТ | Введение в алгебру. Лекция 4: Кольцо многочленов от одной переменной

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать программу

Упражнение 1.13.34. Наибольший общий делитель d(x) многочленов f(x) = 3x⁵-4x⁴+x³-3x²+4x-1 и g(x) = 3x⁵+5x⁴+x³-x²-3x+1 представить в виде d(x)=f(x)u(x)+g(x)v(x), где u(x), v(x) - многочлены степеней, меньших чем степени многочленов g(x) и f(x) соответственно.

Решение. Сначала с помощью алгоритма Евклида находим d(x)=3x³+2x²+2x-1, при этом

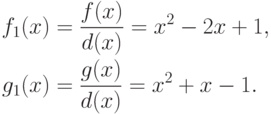
$\begin{align*} f_1(x) &= \frac{f(x)}{d(x)} = x^2-2x+1,\\ g_1(x) &= \frac{g(x)}{d(x)} = x^2+x-1. \end{align*}$

Ищем многочлены u(x) и v(x) такие, что 1=f₁(x)u(x)+g₁(x)v(x).

Так как степени многочленов u(x) и v(x) должны быть меньше двух, то u(x)=ax+b, v(x)=cx+d, где 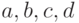$a,b,c,d\inR$ . Приравнивая в коэффициенты при одинаковых степенях переменной x, получаем систему линейных уравнений для a, b, c, d. Решая эту систему, получаем, что a=3, b=5, c=-3, d=4. Итак, d(x)=3x³+2x²+2x-1=f(x)(3x+5)+g(x)(-3x+4).

Определение 1.13.35. Пусть K - поле, $f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\in K[x],\quad a_n,...,a_0\in K$ . Если $c\in K$ , то элемент $f(c)=a_nc^n+a_{n-1}c^{n-1}+...+a_1c+a_0\in K$ назовем значением многочлена f(x) при x=c. Таким образом, получаем отображения: $f: K\to K,\quad c\mapsto f(c)$ (полиномиальная функция, определяемая многочленом f(x) ); $K[x]\to K,\quad f(x)\mapsto f(c)$ (ясно, что если f(x)=g(x) в K[x], то f(c)=g(c) для всех $c\in K$ ).

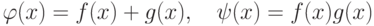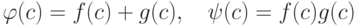Лемма 1.13.36. Если в K[x] $\varphi(x)=f(x)+g(x),\quad \psi(x)=f(x)g(x)$ и $c\in K$ , то $\varphi(c)=f(c)+g(c),\quad \psi(c)=f(c)g(c)$ . Таким образом, отображение $\Delta_c: K[x]\to K,\quad f(x)\mapsto f(c)$ , является гомоморфизмом колец (при этом $\text{Ker}\Delta_c=\{f(x)\in K[x] \mid\allowbreak f(c)=0\}$ ).

Доказательство следует из определения сложения и умножения многочленов в кольце K[x].

Определение 1.13.37. Элемент $c\in K$ называется корнем многочлена $f(x)\in K[x]$ , если f(c)=0 .

Теорема 1.13.38 (Безу). Пусть $c\in K$ . Остаток от деления многочлена f(x) в кольце K[x] на множитель x-c равен значению f(c) многочлена f(x) при x=c.

Доказательство. В силу алгоритма деления f(x)=(x-c)q(x)+r(x), где или r(x)=0, или 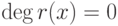$\deg r(x)=0$ , и поэтому 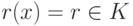$r(x)=r\in K$ . Итак, f(x)=(x-c)q(x)+r, следовательно, f(c)=(c-c)q(c)+r=r, и поэтому f(x)=(x-c)q(x)+f(c).

Следствие 1.13.39. Элемент $c\in K$ является корнем многочлена $f(x)\in K[x]$ тогда и только тогда, когда многочлен f(x) делится на x-c.

Замечание 1.13.40.

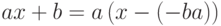Если $a,b\in K$ , $a\ne 0$ , то делимость многочлена $f(x)\in K[x]$ на многочлен $ax+b=a\left(x-\left(-\sfrac{b}{a}\right)\right)$ равносильна делимости на многочлен x-c, 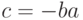$c=-\sfrac{b}{a}$ , и поэтому нахождение корней многочлена $f(x)\in K[x]$ в поле K равносильно нахождению его линейных делителей в кольце K[x].
Если $c\in K$ , $\Delta_c: K[x]\to K$ , $\Delta_c(f)=f(c)$ , то $\text{Ker}\Delta_c=\{f(x)\in K[x]\mid f(c)=0\}= (x-c)K[x]=I_c$ (главный идеал в кольце K[x], порожденный многочленом x-c ).

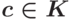Замечание 1.13.41 (схема (алгоритм) Горнера деления многочлена $\boldsymbol{f(x)\in K[x]}$ на линейный многочлен $\boldsymbol{x-c}$ , $\boldsymbol{c\in K}$ )

Пусть $f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\in K[x]$ ,

$\begin{gathe} f(x)=(x-c)q(x)+r,\quad r\in K, \\ q(x)=b_{n-1}x^{n-1}+...+b_1x+b_0\in K[x]. \end{gathe}$

Тогда, приравнивая коэффициенты при xⁿ,x^n-1,...,x,1, соответственно получаем

$\begin{align*} & a_n = b_{n-1}; \\ & a_{n-1}=b_{n-2}-cb_{n-1}; \\ & a_{n-2}=b_{n-3}-cb_{n-2}; \\[-1pt] & ... \\[-1pt] & a_k = b_{k-1}-cb_k; \\[-1pt] & ... \\[-1pt] & a_1=b_0-cb_1; \\ & a_0=r-cb_0. \end{align*}$

Пересчитывая, получаем

$\begin{align*} & b_{n-1}=a_n; \\ & b_{n-2}=cb_{n-1}+a_{n-1}; \\ & b_{n-3}=cb_{n-2}+a_{n-2}; \\[-1pt] & ... \\[-1pt] & b_{k-1}=cb_k+a_k; \\[-1pt] & ... \\[-1pt] & b_0=cb_1+a_1; \\ & r=cb_0+a_0. \end{align*}$

Таким образом, коэффициенты частного b_n-1,...,b₁,b₀ и остаток r=f(c) последовательно вычисляются по коэффициентам a_n,...,a₁,a₀ и элементу c, если использовать однотипную процедуру

Пример 1.13.42. Пусть f(x)=2x⁴-x²+3x-2, c=-2. Тогда

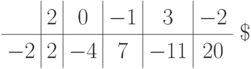
$\renewcommand{\arraystretch}{1.2} \begin{array}{c|c|c|c|c|c} & 2 & 0 & -1 & 3 & -2 \\ \hline -2 & 2 & -4 & 7 & -11 & 20 \end{array}\ \$

поэтому f(x)=(x+2)q(x)+20, где q(x)=(x+2)(2x³-4x²+7x-11).

Замечание 1.13.43.

Схема Горнера дает быстрый алгоритм вычисления значения r=f(c) многочлена $f(x)\in K[x]$ в точке c (минимизируя число умножений).
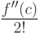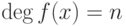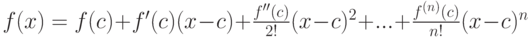Последовательное применение схемы Горнера позволяет построить эффективный алгоритм записи многочлена f(x) в виде формулы Тейлора по степеням (x-c). А именно, при первом применении схемы Горнера крайний правый коэффициент равен f(c), при втором применении крайний справа коэффициент равен f'(c), при третьем - $\frac{f''(c)}{2!}$ , и так далее. Таким образом, если $\deg f(x)=n$ , то $f(x)=f(c)+f'(c)(x-c)+\frac{f''(c)}{2!}(x-c)^2+...+ \frac{f^{(n)}(c)}{n!}(x-c)^n$ (формула Тейлора).

Например, для f(x)=x⁴-6x³-2x²+5x-4 и c=5 имеем

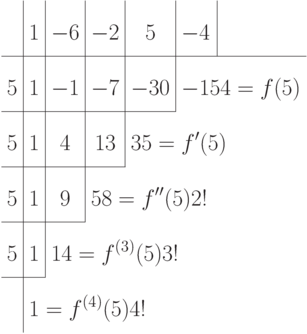
$\renewcommand{\arraystretch}{2} \begin{array}{c|c|c|c|c|l} & 1 & -6 & -2 & 5 & -4\ \vline \\ \cline{1-6} 5 & 1 & -1 & -7 & -30 & -154=f(5) \\ \cline{1-5} 5 & 1 & 4 & 13 & \multicolumn{2}{l}{\lefteqn{35=f'(5)}} \\ \cline{1-4} 5 & 1 & 9 & \multicolumn{3}{l}{\lefteqn{58=\sfrac{f''(5)}{2!}}} \\ \cline{1-3} 5 & 1 & \multicolumn{4}{l}{\lefteqn{14=\sfrac{f^{(3)}(5)}{3!}}} \\ \cline{1-2} & \multicolumn{5}{l}{1=\lefteqn{\sfrac{f^{(4)}(5)}{4!}}} \end{array}$

Таким образом, f(x)=(x-5)⁴+14(x-5)³+58(x-5)²+35(x-5)-154.

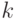Определение 1.13.44.Пусть $f(x)\in K[x]$ , $c\in K$ , и c - корень многочлена f(x), т. е. f(c)=0. По теореме Безу многочлен f(x) делится на x-c. Возможно, многочлен f(x) делится на более высокие степени многочлена x-c. Пусть $k\inN$ - такое натуральное число, что f(x) делится на (x-c)^k, но не делится на (x-c)^k+1, поэтому 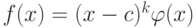$f(x)=(x-c)^k \varphi(x)$ , многочлен $\varphi(x)\in K[x]$ уже не делится на x-c (это равносильно тому, что $\varphi(c)\ne 0$ ). В этом случае число k назовем кратностью корня c многочлена f(x), а сам корень c - k -кратным корнем многочлена f(x). Если k=1, то корень c называется простым корнем многочлена f(x).

Замечание 1.13.45. Понятие абстрактного линейного пространства мы детально рассмотрим в "Линейное пространство строк над полем" , после того как изучим ряд конкретных линейных пространств.

Понятие алгебры над полем (как кольца, являющегося к тому же и линейным пространством) будет рассмотрено в "Cтупенчатые системы линейных уравнений и метод Гаусса" .

Дальше >>

Введение в алгебру

Введение в алгебру

Кольцо многочленов от одной переменной

Вопросы и ответы

Студенты

Авторизоваться

Введение в алгебру

Введение в алгебру

Кольцо многочленов от одной переменной

Вопросы и ответы

Студенты